Chybová funkce - Error function

V matematice je chybová funkce (také nazývaná Gaussova chybová funkce ), často označovaná erf , komplexní funkcí komplexní proměnné definované jako:

${\ displaystyle \ operatorname {erf} z = {\ frac {2} {\ sqrt {\ pi}}} \ int _ {0}^{z} e^{-t^{2}} \, dt.}$

Tento integrál je speciální ( neelementární ) sigmoidní funkce, která se často vyskytuje v pravděpodobnosti , statistikách a parciálních diferenciálních rovnicích . V mnoha těchto aplikacích je argument funkce skutečným číslem. Pokud je argument funkce skutečný, pak je také funkční hodnota.

Ve statistikách má pro nezáporné hodnoty x chybová funkce následující interpretaci: pro náhodnou proměnnou Y, která je normálně rozdělena se střední hodnotou 0 a standardní odchylkou 1/√ 2, erf x je pravděpodobnost, že Y spadá do rozsahu [ - x , x ] .

Dvě úzce související funkce jsou komplementární chybová funkce ( erfc ) definovaná jako

${\ displaystyle \ operatorname {erfc} z = 1- \ operatorname {erf} z,}$

a imaginární chybová funkce ( erfi ) definovaná jako

${\ displaystyle \ operatorname {erfi} z = -i \ operatorname {erf} iz,}$

kde i je imaginární jednotka .

název

Název „chybová funkce“ a jeho zkratka erf navrhl JWL Glaisher v roce 1871 kvůli jeho spojení s „teorií pravděpodobnosti a zejména teorií chyb “. Doplněk chybové funkce byl také diskutován Glaisherem v samostatné publikaci ve stejném roce. Pro „zákon facility“ chyb, jejichž hustota je dána vztahem

${\ Displaystyle f (x) = \ left ({\ frac {c} {\ pi}} \ right)^{\ frac {1} {2}} e^{-cx^{2}}}$

( normální rozdělení ), Glaisher vypočítá pravděpodobnost chyby ležící mezi p a q jako:

${\ Displaystyle \ left ({\ frac {c} {\ pi}} \ right)^{\ frac {1} {2}} \ int _ {p}^{q} e^{-cx^{2} } \, dx = {\ tfrac {1} {2}} \ left (\ operatorname {erf} \ left (q {\ sqrt {c}} \ right)-\ operatorname {erf} \ left (p {\ sqrt {c}} \ right) \ right).}$

Aplikace

Když jsou výsledky řady měření popsány normálním rozložením se standardní odchylkou σ a očekávanou hodnotou 0, pak erf (A/σ √ 2) Je pravděpodobnost, že chyba jediného měření se pohybuje mezi - a + , pro pozitivní A . To je užitečné například při určování bitové chybovosti digitálního komunikačního systému.

Chybové a komplementární chybové funkce se vyskytují například v řešeních tepelné rovnice, když jsou okrajové podmínky dány funkcí Heaviside step .

Chybovou funkci a její aproximace lze použít k odhadu výsledků, které platí s vysokou pravděpodobností nebo s nízkou pravděpodobností. Vzhledem k náhodné veličině X ~ Norm [ μ , σ ] (normální rozdělení se středním μ a standardní odchylkou σ ) a konstantě L < μ :

${\ displaystyle {\ begin {aligned} \ Pr [X \ leq L] & = {\ frac {1} {2}}+{\ frac {1} {2}} \ operatorname {erf} {\ frac {L -\ mu} {{\ sqrt {2}} \ sigma}} \\ & \ cca A \ exp \ left (-B \ left ({\ frac {L- \ mu} {\ sigma}} \ right)^ {2} \ right) \ end {aligned}}}$

kde A a B jsou určité číselné konstanty. Pokud je L dostatečně daleko od průměru, konkrétně μ - L ≥ σ √ ln k , pak:

${\ Displaystyle \ Pr [X \ leq L] \ leq A \ exp (-B \ ln {k}) = {\ frac {A} {k^{B}}}}$

pravděpodobnost tedy jde na 0 jako k → ∞ .

Pravděpodobnost, že X je v intervalu [ L _a , L _b ], lze odvodit jako

${\ Displaystyle {\ begin {aligned} \ Pr [L_ {a} \ leq X \ leq L_ {b}] & = \ int _ {L_ {a}}^{L_ {b}} {\ frac {1} {{\ sqrt {2 \ pi}} \ sigma}} \ exp \ left (-{\ frac {(x- \ mu) ^{2}} {2 \ sigma ^{2}}} \ right) \, dx \\ & = {\ frac {1} {2}} \ left (\ operatorname {erf} {\ frac {L_ {b}-\ mu} {{\ sqrt {2}} \ sigma}}-\ operatorname {erf} {\ frac {L_ {a}-\ mu} {{\ sqrt {2}} \ sigma}} \ right). \ end {aligned}}}$

Vlastnosti

Vlastnost erf ( - z ) = −erf z znamená, že chybová funkce je lichá funkce . To přímo vyplývá ze skutečnosti, že integrand e ^{- t 2} je sudá funkce (integrace sudé funkce dává lichou funkci a naopak).

Pro jakékoli komplexní číslo z :

${\ displaystyle \ operatorname {erf} {\ overline {z}} = {\ overline {\ operatorname {erf} z}}}$

kde z je komplexně sdružená z Z .

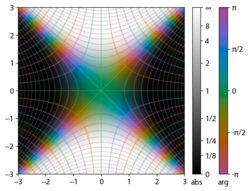
Integrand f = exp ( -z ² ) a f = erf z jsou zobrazeny v komplexní z -rovině na obrázcích vpravo s vybarvením domény .

Chybová funkce v +∞ je přesně 1 (viz Gaussův integrál ). Na skutečné ose se erf z blíží jednotě na z → +∞ a −1 při z → −∞ . Na pomyslné ose má tendenci k ± i ∞ .

Taylorova řada

Chybová funkce je celá funkce ; nemá žádné singularity (kromě toho, že v nekonečnu) a jeho Taylorova expanze vždy konverguje, ale je skvěle známá „[...] pro svou špatnou konvergenci, pokud x > 1 “.

Definující integrál nelze vyhodnotit v uzavřené formě, pokud jde o elementární funkce , ale rozšířením integrandu e ^{- z 2} do jeho řady Maclaurin a integrací termínu po výrazu získáme řadu Maclaurin chybové funkce jako:

${\ displaystyle {\ begin {aligned} \ operatorname {erf} z & = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0}^{\ infty} {\ frac {(- 1)^{n} z^{2n+1}} {n! (2n+1)}} \ \ [6pt] & = {\ frac {2} {\ sqrt {\ pi}}} \ left (z -{\ frac {z^{3}} {3}}+{\ frac {z^{5}} {10}}-{\ frac {z^{7}} {42}}+{\ frac { z^{9}} {216}}-\ cdots \ right) \ end {aligned}}}$

který platí pro každé komplexní číslo  z . Pojmy jmenovatele jsou sekvence (sekvence A007680 v OEIS ) v OEIS .

Pro iterační výpočet výše uvedené řady může být užitečná následující alternativní formulace:

${\ Displaystyle {\ begin {aligned} \ operatorname {erf} z & = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0}^{\ infty} \ left (z \ prod _ {k = 1}^{n} {\ frac {-(2k-1) z^{2}} {k (2k+1)}} \ right) \\ [6pt] & = {\ frac {2 } {\ sqrt {\ pi}}} \ sum _ {n = 0}^{\ infty} {\ frac {z} {2n+1}} \ prod _ {k = 1}^{n} {\ frac {-z^{2}} {k}} \ end {aligned}}}$

protože - (2 k - 1) z ²/k (2 k + 1)vyjadřuje multiplikátor k přeměně k -tého členu na ( k  + 1) -tý člen (s ohledem na z jako první člen).

Funkce imaginární chyby má velmi podobnou řadu Maclaurin, která je:

${\ displaystyle {\ begin {aligned} \ operatorname {erfi} z & = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0}^{\ infty} {\ frac {z^ {2n+1}} {n! (2n+1)}} \\ [6pt] & = {\ frac {2} {\ sqrt {\ pi}}} \ left (z+{\ frac {z^{3 }} {3}}+{\ frac {z^{5}} {10}}+{\ frac {z^{7}} {42}}+{\ frac {z^{9}} {216} }+\ cdots \ right) \ end {zarovnaný}}}$

který platí pro každé komplexní číslo  z .

Derivát a integrál

Derivace chybové funkce vyplývá bezprostředně z její definice:

${\ displaystyle {\ frac {d} {dz}} \ operatorname {erf} z = {\ frac {2} {\ sqrt {\ pi}}} e^{-z^{2}}.}$

Z toho je derivace imaginární chybové funkce také okamžitá:

${\ displaystyle {\ frac {d} {dz}} \ operatorname {erfi} z = {\ frac {2} {\ sqrt {\ pi}}} e^{z^{2}}.}$

Primitivní funkce chyb, který lze získat integrací per partes , je

${\ displaystyle z \ operatorname {erf} z+{\ frac {e^{-z^{2}}} {\ sqrt {\ pi}}}.}$

Antiderivativum imaginární chybové funkce, které lze také získat integrací po částech, je

${\ displaystyle z \ operatorname {erfi} z-{\ frac {e^{z^{2}}} {\ sqrt {\ pi}}}.}$

Deriváty vyššího řádu jsou dány znakem

${\ displaystyle \ operatorname {erf} ^{(k)} z = {\ frac {2 (-1) ^{k-1}} {\ sqrt {\ pi}}} {\ mathit {H}} _ { k-1} (z) e^{-z^{2}} = {\ frac {2} {\ sqrt {\ pi}}} {\ frac {d^{k-1}} {dz^{k -1}}} \ left (e^{-z^{2}} \ right), \ qquad k = 1,2, \ dots}$

kde H jsou hermitské polynomy fyziků .

Řada Bürmann

Expanze, která konverguje rychleji pro všechny skutečné hodnoty x než Taylorova expanze, se získá pomocí věty Hanse Heinricha Bürmanna :

${\ displaystyle {\ begin {aligned} \ operatorname {erf} x & = {\ frac {2} {\ sqrt {\ pi}}} \ operatorname {sgn} x \ cdot {\ sqrt {1-e^{-x ^{2}}}} \ left (1-{\ frac {1} {12}} \ left (1-e^{-x^{2}} \ right)-{\ frac {7} {480} } \ left (1-e^{-x^{2}} \ right)^{2}-{\ frac {5} {896}} \ left (1-e^{-x^{2}} \ vpravo)^{3}-{\ frac {787} {276480}} \ left (1-e^{-x^{2}} \ right)^{4}-\ cdots \ right) \\ [10pt] & = {\ frac {2} {\ sqrt {\ pi}}} \ operatorname {sgn} x \ cdot {\ sqrt {1-e^{-x^{2}}}} \ left ({\ frac { \ sqrt {\ pi}} {2}}+\ sum _ {k = 1}^{\ infty} c_ {k} e^{-kx^{2}} \ right). \ end {aligned}}}$

kde sgn je znaková funkce . Ponecháním pouze prvních dvou koeficientů a zvolením c ₁ =31/200a c ₂ = -341/8000, výsledná aproximace ukazuje svou největší relativní chybu při x = ± 1,3796 , kde je menší než 0,0036127:

${\ displaystyle \ operatorname {erf} x \ zhruba {\ frac {2} {\ sqrt {\ pi}}} \ operatorname {sgn} x \ cdot {\ sqrt {1-e^{-x^{2}} }} \ left ({\ frac {\ sqrt {\ pi}} {2}}+{\ frac {31} {200}} e^{-x^{2}}-{\ frac {341} {8000 }} e^{-2x^{2}} \ vpravo).}$

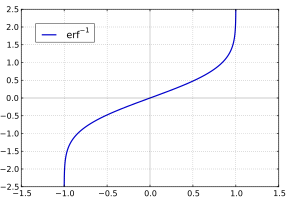
Inverzní funkce

Vzhledem ke komplexnímu číslu z neexistuje jedinečné komplexní číslo w splňující erf w = z , takže skutečná inverzní funkce by byla vícehodnotová. Pro −1 < x <1 však existuje jedinečné skutečné číslo označené jako erf ⁻¹ x uspokojující

${\ displaystyle \ operatorname {erf} \ left (\ operatorname {erf} ^{-1} x \ right) = x.}$

Funkce inverzní chyby je obvykle definována s doménou (−1,1) a je omezena na tuto doménu v mnoha systémech počítačové algebry. Lze jej však rozšířit na disk | z | <1 komplexní roviny pomocí Maclaurinovy ​​řady

${\ displaystyle \ operatorname {erf} ^{-1} z = \ sum _ {k = 0} ^{\ infty} {\ frac {c_ {k}} {2k+1}} \ left ({\ frac { \ sqrt {\ pi}} {2}} z \ right)^{2k+1},}$

kde c ₀ = 1 a

${\ Displaystyle {\ begin {aligned} c_ {k} & = \ sum _ {m = 0}^{k-1} {\ frac {c_ {m} c_ {k-1-m}} {(m+ 1) (2m+1)}} \\ & = \ left \ {1,1, {\ frac {7} {6}}, {\ frac {127} {90}}, {\ frac {4369} { 2520}}, {\ frac {34807} {16200}}, \ ldots \ right \}. \ End {aligned}}}$

Máme tedy rozšíření řady (společné faktory byly z čitatelů a jmenovatelů zrušeny):

${\ displaystyle \ operatorname {erf} ^{-1} z = {\ frac {\ sqrt {\ pi}} {2}} \ left (z+{\ frac {\ pi} {12}} z ^{3} +{\ frac {7 \ pi ^{2}} {480}} z ^{5}+{\ frac {127 \ pi ^{3}} {40320}} z ^{7}+{\ frac {4369 \ pi ^{4}} {5806080}} z ^{9}+{\ frac {34807 \ pi ^{5}} {182476800}} z ^{11}+\ cdots \ right).}$

(Po zrušení jsou zlomky čitatele / jmenovatele položky OEIS :  A092676 / OEIS :  A092677 v OEIS ; bez zrušení jsou podmínky čitatele uvedeny v položce OEIS :  A002067 .) Hodnota chybové funkce na  ± ∞ se rovná  ± 1 .

Pro | z | <1 , máme erf (erf ⁻¹ z ) = z .

Funkce inverzní komplementární chyby je definována jako

${\ displaystyle \ operatorname {erfc} ^{-1} (1-z) = \ operatorname {erf} ^{-1} z.}$

Pro reálné x existuje jedinečné skutečné číslo erfi ⁻¹ x uspokojující erfi (erfi ⁻¹ x ) = x . Funkce inverzní imaginární chyby je definována jako erfi ⁻¹ x .

Pro skutečný x , Newtonova metoda může být použita pro výpočet erfi ^-1 x , a -1 ≤ x nejvýše 1 , následující řada konverguje Maclaurinův:

${\ displaystyle \ operatorname {erfi}^{-1} z = \ sum _ {k = 0}^{\ infty} {\ frac {(-1)^{k} c_ {k}} {2k+1} } \ left ({\ frac {\ sqrt {\ pi}} {2}} z \ right)^{2k+1},}$

kde c _k je definováno výše.

Asymptotická expanze

Užitečné asymptotické rozšíření komplementární chybové funkce (a tedy i chybové funkce) pro velká reálná x je

${\ Displaystyle {\ begin {aligned} \ operatorname {erfc} x & = {\ frac {e^{-x^{2}}} {x {\ sqrt {\ pi}}}} \ left (1+ \ sum _ {n = 1}^{\ infty} (-1)^{n} {\ frac {1 \ cdot 3 \ cdot 5 \ cdots (2n-1)} {\ left (2x^{2} \ right) ^{n}}} \ right) \\ [6pt] & = {\ frac {e^{-x^{2}}} {x {\ sqrt {\ pi}}}}} \ sum _ {n = 0 }^{\ infty} (-1)^{n} {\ frac {(2n-1) !!} {\ left (2x^{2} \ right)^{n}}}, \ end {zarovnaný} }}$

kde (2 n - 1) !! je dvojitý faktoriál z (2 n - 1) , což je produkt všech lichých čísel až (2 n - 1) . Tato řada se liší pro každé konečné x a její význam jako asymptotické expanze je ten, že pro jakékoli celé číslo N ≥ 1 má

${\ displaystyle \ operatorname {erfc} x = {\ frac {e^{-x^{2}}} {x {\ sqrt {\ pi}}}} \ sum _ {n = 0}^{N-1 } (-1)^{n} {\ frac {(2n-1) !!} {\ left (2x^{2} \ right)^{n}}}+R_ {N} (x)}$

kde zbytek v Landau notace , je

${\ Displaystyle R_ {N} (x) = O \ left (x^{-(1+2N)} e^{-x^{2}} \ right)}$

jako x → ∞ .

Přesná hodnota zbytku je skutečně

${\ Displaystyle R_ {N} (x): = {\ frac {(-1)^{N}} {\ sqrt {\ pi}}} 2^{1-2N} {\ frac {(2N)!} {N!}} \ Int _ {x}^{\ infty} t^{-2N} e^{-t^{2}} \, dt,}$

což snadno následuje indukcí, psaním

${\ Displaystyle e^{-t^{2}} =-(2t)^{-1} \ left (e^{-t^{2}} \ right) '}$

a integrace po částech.

Pro dostatečně velké hodnoty x je k získání dobré aproximace erfc x zapotřebí pouze několik prvních členů této asymptotické expanze (zatímco pro ne příliš velké hodnoty x poskytuje výše uvedená Taylorova expanze v 0 velmi rychlou konvergenci).

Pokračující rozšiřování frakce

Řetězový zlomek expanze funkce komplementární chybové je:

${\ displaystyle \ operatorname {erfc} z = {\ frac {z} {\ sqrt {\ pi}}} e^{-z^{2}} {\ cfrac {1} {z^{2}+{\ cfrac {a_ {1}} {1+{\ cfrac {a_ {2}} {z^{2}+{\ cfrac {a_ {3}} {1+ \ dotsb}}}}}}}}}, \ qquad a_ {m} = {\ frac {m} {2}}.}$

Integrál chybové funkce s funkcí Gaussovy hustoty

${\ Displaystyle \ int _ {-\ infty} ^{\ infty} \ operatorname {erf} \ left (ax+b \ right) {\ frac {1} {\ sqrt {2 \ pi \ sigma ^{2}} }} \ exp \ left (-{\ frac {(x- \ mu) ^{2}} {2 \ sigma ^{2}}} \ right) \, dx = \ operatorname {erf} {\ frac {a \ mu +b} {\ sqrt {1 +2a ^{2} \ sigma ^{2}}}}, \ qquad a, b, \ mu, \ sigma \ in \ mathbb {R}}$

který vypadá, že souvisí s Ng a Gellerem, vzorec 13 v sekci 4.3 se změnou proměnných.

Faktoriální řada

Inverzní faktoriální řada :

${\ Displaystyle {\ begin {aligned} \ operatorname {erfc} z & = {\ frac {e^{-z^{2}}} {{\ sqrt {\ pi}} \, z}} \ sum _ {n = 0}^{\ infty} {\ frac {(-1)^{n} Q_ {n}} {{(z^{2} +1)}^{\ bar {n}}}} \\ & = {\ frac {e^{-z^{2}}} {{\ sqrt {\ pi}} \, z}} \ left (1-{\ frac {1} {2}} {\ frac {1 } {(z^{2} +1)}}+{\ frac {1} {4}} {\ frac {1} {(z^{2} +1) (z^{2} +2)} }-\ cdots \ right) \ end {aligned}}}$

konverguje pro Re ( z ² )> 0 . Tady

${\ displaystyle {\ begin {aligned} Q_ {n} & {\ overset {\ text {def}} {{} = {}}} {\ frac {1} {\ Gamma \ left ({\ frac {1} {2}} \ right)}} \ int _ {0} ^{\ infty} \ tau (\ tau -1) \ cdots (\ tau -n+1) \ tau ^{ -{\ frac {1} { 2}}} e^{-\ tau} \, d \ tau \\ & = \ sum _ {k = 0}^{n} \ left ({\ tfrac {1} {2}} \ right)^{ \ bar {k}} s (n, k), \ end {aligned}}}$

z ⁿ označuje rostoucí faktoriál a s ( n , k ) označuje podepsané Stirlingovo číslo prvního druhu . Existuje také zastoupení nekonečným součtem obsahujícím dvojitý faktoriál :

${\ displaystyle \ operatorname {erf} z = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0}^{\ infty} {\ frac {(-2)^{n} (2n-1) !!} {(2n+1)!}} Z^{2n+1}}$

Numerické aproximace

Aproximace s elementárními funkcemi

• Abramowitz a Stegun uvádějí několik aproximací s různou přesností (rovnice 7.1.25–28). To umožňuje zvolit nejrychlejší aproximaci vhodnou pro danou aplikaci. Aby se zvýšila přesnost, jsou to:

  ${\ displaystyle \ operatorname {erf} x \ cca 1-{\ frac {1} {\ left (1+a_ {1} x+a_ {2} x^{2}+a_ {3} x^{3} +a_ {4} x^{4} \ right)^{4}}}, \ qquad x \ geq 0}$

  (maximální chyba: 5 × 10 ⁻⁴ )

  kde a ₁ = 0,278393 , a ₂ = 0,230389 , a ₃ = 0,000972 , a ₄ = 0,078108

  ${\ displaystyle \ operatorname {erf} x \ cca 1- \ left (a_ {1} t+a_ {2} t^{2}+a_ {3} t^{3} \ right) e^{-x^ {2}}, \ quad t = {\ frac {1} {1+px}}, \ qquad x \ geq 0}$

  (maximální chyba: 2,5 × 10 ⁻⁵ )

  kde p = 0,47047 , a ₁ = 0,3480242 , a ₂ = −0,0958798 , a ₃ = 0,7478556

  $${\ Displaystyle \ operatorname {erf} x \ cca 1-{\ frac {1} {\ left (1+a_ {1} x+a_ {2} x^{2}+\ cdots+a_ {6} x^ {6} \ right)^{16}}}, \ qquad x \ geq 0}$$

  
  (maximální chyba: 3 × 10 ⁻⁷ )

  kde a ₁ = 0,0705230784 , a ₂ = 0,0422820123 , a ₃ = 0,0092705272 , a ₄ = 0,0001520143 , a ₅ = 0,0002765672 , a ₆ = 0,0000430638

  $${\ displaystyle \ operatorname {erf} x \ cca 1- \ left (a_ {1} t+a_ {2} t^{2}+\ cdots+a_ {5} t^{5} \ right) e^{ -x^{2}}, \ quad t = {\ frac {1} {1+px}}}$$

  
  (maximální chyba: 1,5 × 10 ⁻⁷ )

  kde p = 0,3275911 , a ₁ = 0,254829592 , a ₂ = −0,284496736 , a ₃ = 1,421413741 , a ₄ = −1,453152027 , a ₅ = 1,061405429

  Všechny tyto aproximace platí pro x ≥ 0 . Chcete -li použít tyto aproximace pro záporné x , použijte fakt, že erf x je lichá funkce, takže erf x = −erf ( - x ) .
• Exponenciální hranice a čistá exponenciální aproximace pro komplementární chybovou funkci jsou dány vztahem

  ${\ displaystyle {\ begin {aligned} \ operatorname {erfc} x & \ leq {\ tfrac {1} {2}} e^{-2x^{2}}+{\ tfrac {1} {2}} e^ {-x^{2}} \ leq e^{-x^{2}}, & \ quad x &> 0 \\\ operatorname {erfc} x & \ zhruba {\ tfrac {1} {6}} e^{ -x^{2}}+{\ tfrac {1} {2}} e^{-{\ frac {4} {3}} x^{2}}, & \ quad x &> 0. \ end {zarovnáno }}}$

• Výše uvedené byly zobecněny na součty N exponenciálů se zvyšující se přesností ve smyslu N, takže erfc x lze přesně aproximovat nebo ohraničit 2 Q̃ ( √ 2 x ) , kde

  ${\ Displaystyle {\ tilde {Q}} (x) = \ sum _ {n = 1}^{N} a_ {n} e^{-b_ {n} x^{2}}.}$

  Zejména existuje systematická metodika řešení numerických koeficientů {( a _n , b _n )}^N
  _{n = 1}které přinášejí aproximaci minimaxu nebo jsou vázány na úzce související funkci Q : Q ( x ) ≈ Q̃ ( x ) , Q ( x ) ≤ Q̃ ( x ) nebo Q ( x ) ≥ Q̃ ( x ) pro x ≥ 0 . Koeficienty {( a _n , b _n )}^N
  _{n = 1}pro mnoho variací exponenciálních aproximací a hranic až N = 25 byly uvolněny k otevřenému přístupu jako komplexní datová sada.
• Těsnou aproximaci komplementární chybové funkce pro x ∈ [0, ∞) uvádí Karagiannidis & Lioumpas (2007), který pro vhodnou volbu parametrů { A , B } ukázal , že

  ${\ displaystyle \ operatorname {erfc} x \ zhruba {\ frac {\ left (1-e^{-Ax} \ right) e^{-x^{2}}} {B {\ sqrt {\ pi}} X}}.}$

  Zjistili { A , B } = {1.98,1.135} , který dal dobré přiblížení pro všechny x ≥ 0 . K dispozici jsou také alternativní koeficienty pro přizpůsobení přesnosti pro konkrétní aplikaci nebo pro transformaci výrazu do těsné vazby.
• Jednorázová dolní hranice je

  $${\ displaystyle \ operatorname {erfc} x \ geq {\ sqrt {\ frac {2e} {\ pi}}} {\ frac {\ sqrt {\ beta -1}} {\ beta}} e^{ -\ beta x^{2}}, \ qquad x \ geq 0, \ quad \ beta> 1,}$$

  

  kde parametr β lze vybrat, aby se minimalizovala chyba v požadovaném intervalu aproximace.
• Další přiblížení uvádí Sergej Winitzki pomocí svých „globálních Padéových aproximací“:

  ${\ displaystyle \ operatorname {erf} x \ zhruba \ operatorname {sgn} x \ cdot {\ sqrt {1- \ exp \ left (-x^{2} {\ frac {{\ frac {4} {\ pi} }+sekera^{2}} {1+sekera^{2}}} \ vpravo)}}}$

  kde

  ${\ Displaystyle a = {\ frac {8 (\ pi -3)} {3 \ pi (4- \ pi)}} \ cca 0,140012.}$

  Toto je navrženo tak, aby bylo velmi přesné v sousedství 0 a okolí nekonečna a relativní chyba je menší než 0,00035 pro všechna reálná x . Použitím alternativní hodnoty a ≈ 0,147 se sníží maximální relativní chyba na přibližně 0,00013.

  Tuto aproximaci lze převrátit, aby se získala aproximace pro funkci inverzní chyby:

  ${\ displaystyle \ operatorname {erf} ^{-1} x \ cca \ operatorname {sgn} x \ cdot {\ sqrt {{\ sqrt {\ left ({\ frac {2} {\ pi a}}+{\ frac {\ ln \ left (1-x^{2} \ right)} {2}} \ right)^{2}-{\ frac {\ ln \ left (1-x^{2} \ right)} {a}}}}-\ left ({\ frac {2} {\ pi a}}+{\ frac {\ ln \ left (1-x^{2} \ right)} {2}} \ right) }}.}$

• Aproximace s maximální chybou 1,2 × 10 ⁻⁷ pro jakýkoli skutečný argument je:

  ${\ displaystyle \ operatorname {erf} x = {\ begin {cases} 1- \ tau & x \ geq 0 \\\ tau -1 & x <0 \ end {cases}}}$

  s

  ${\ Displaystyle {\ begin {aligned} \ tau & = t \ cdot \ exp \ left (-x^{2} -1,26551223+1,00002368t+0,37409196t^{2}+0,09678418t^{3} -0,18628806t^ {4} \ right. \\ & \ left. \ Qquad \ qquad \ qquad+0,27886807t^{5} -1,13520398t^{6}+1,48851587t^{7} -0,82215223t^{8}+0,17087277t^ {9} \ right) \ end {aligned}}}$

  a

  ${\ displaystyle t = {\ frac {1} {1+{\ frac {1} {2}} | x |}}.}$

Tabulka hodnot

X	erf x	1 - erf x
0	0	1
0,02	0,022 564 575	0,977 435 425
0,04	0,045 111 106	0,954 888 894
0,06	0,067 621 594	0,932 378 406
0,08	0,090 078 126	0,909 921 874
0,1	0,112 462 916	0,887 537 084
0,2	0,222 702 589	0,777 297 411
0,3	0,328 626 759	0,671 373 241
0,4	0,428 392 355	0,571 607 645
0,5	0,520 499 878	0,479 500 122
0,6	0,603 856 091	0,396 143 909
0,7	0,677 801 194	0,322 198 806
0,8	0,742 100 965	0,257 899 035
0,9	0,796 908 212	0,203 091 788
1	0,842 700 793	0,157 299 207
1.1	0,880 205 070	0,119 794 930
1.2	0,910 313 978	0,089 686 022
1.3	0,934 007 945	0,065 992 055
1.4	0,952 285 120	0,047 714 880
1.5	0,966 105 146	0,033 894 854
1.6	0,976 348 383	0.023 651 617
1.7	0,983 790 459	0,016 209 541
1,8	0,989 090 502	0,010 909 498
1.9	0,992 790 429	0,007 209 571
2	0,995 322 265	0,004 677 735
2.1	0,997 020 533	0,002 979 467
2.2	0,998 137 154	0,001 862 846
2.3	0,998 856 823	0,001 143 177
2.4	0,999 311 486	0,000 688 514
2.5	0,999 593 048	0,000 406 952
3	0,999 977 910	0,000 022 090
3.5	0,999 999 257	0,000 000 743

Související funkce

Komplementární chybová funkce

Funkce komplementární chyba , označený ERFC , je definován jako

${\ displaystyle {\ begin {aligned} \ operatorname {erfc} x & = 1- \ operatorname {erf} x \\ [5pt] & = {\ frac {2} {\ sqrt {\ pi}}} \ int _ { x}^{\ infty} e^{-t^{2}} \, dt \\ [5pt] & = e^{-x^{2}} \ operatorname {erfcx} x, \ end {aligned}} }$

který také definuje erfcx , škálovanou komplementární chybovou funkci (kterou lze použít místo erfc, aby se zabránilo aritmetickému podtečení ). Další forma erfc x pro x ≥ 0 je známá jako Craigův vzorec po jeho objeviteli:

${\ displaystyle \ operatorname {erfc} (x \ mid x \ geq 0) = {\ frac {2} {\ pi}} \ int _ {0}^{\ frac {\ pi} {2}} \ exp \ vlevo (-{\ frac {x ^{2}} {\ sin ^{2} \ theta}} \ right) \, d \ theta.}$

Tento výraz je platný pouze pro kladné hodnoty x , ale lze jej použít ve spojení s erfc x = 2 - erfc ( - x ) k získání erfc ( x ) pro záporné hodnoty. Tato forma je výhodná v tom, že rozsah integrace je pevný a konečný. Rozšíření tohoto výrazu pro erfc součtu dvou nezáporných proměnných je následující:

${\ displaystyle \ operatorname {erfc} (x+y \ mid x, y \ geq 0) = {\ frac {2} {\ pi}} \ int _ {0}^{\ frac {\ pi} {2} } \ exp \ left (-{\ frac {x ^{2}} {\ sin ^{2} \ theta}}-{\ frac {y ^{2}} {\ cos ^{2} \ theta}} \ right) \, d \ theta.}$

Funkce imaginární chyby

Funkce imaginární chyby , označovaná jako erfi , je definována jako

${\ displaystyle {\ begin {aligned} \ operatorname {erfi} x & =-i \ operatorname {erf} ix \\ [5pt] & = {\ frac {2} {\ sqrt {\ pi}}} \ int _ { 0}^{x} e^{t^{2}} \, dt \\ [5pt] & = {\ frac {2} {\ sqrt {\ pi}}} e^{x^{2}} D (x), \ end {aligned}}}$

kde D ( x ) je Dawsonova funkce (kterou lze použít místo erfi, aby se zabránilo aritmetickému přetečení ).

Navzdory názvu „funkce imaginární chyby“ je erfi x skutečné, když x je skutečné.

Když je chybová funkce vyhodnocena pro libovolné komplexní argumenty z , výsledná komplexní chybová funkce je obvykle diskutována v měřítku jako funkce Faddeeva :

${\ Displaystyle w (z) = e^{-z^{2}} \ operatorname {erfc} (-iz) = \ operatorname {erfcx} (-iz).}$

Kumulativní distribuční funkce

Chybová funkce je v podstatě shodná se standardní normální kumulativní distribuční funkcí , označovanou Φ , některými softwarovými jazyky také pojmenovanou normou ( x ) , protože se liší pouze škálováním a překladem. Vskutku,

${\ Displaystyle {\ begin {aligned} \ Phi (x) & = {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {-\ infty}^{x} e^{\ tfrac { -t^{2}} {2}} \, dt \\ [6pt] & = {\ frac {1} {2}} \ left (1+ \ operatorname {erf} {\ frac {x} {\ sqrt {2}}} \ right) \\ [6pt] & = {\ frac {1} {2}} \ operatorname {erfc} \ left (-{\ frac {x} {\ sqrt {2}}} \ right ) \ end {aligned}}}$

nebo přeskupené na erf a erfc :

${\ Displaystyle {\ begin {aligned} \ operatorname {erf} (x) & = 2 \ Phi \ left (x {\ sqrt {2}} \ right) -1 \\ [6pt] \ operatorname {erfc} (x ) & = 2 \ Phi \ left (-x {\ sqrt {2}} \ right) \\ & = 2 \ left (1- \ Phi \ left (x {\ sqrt {2}} \ right) \ right) . \ end {aligned}}}$

V důsledku toho je chybová funkce také úzce spjata s funkcí Q , což je ocasní pravděpodobnost standardního normálního rozdělení. Funkci Q lze vyjádřit pomocí chybové funkce jako

${\ displaystyle {\ begin {aligned} Q (x) & = {\ frac {1} {2}}-{\ frac {1} {2}} \ operatorname {erf} {\ frac {x} {\ sqrt {2}}} \\ & = {\ frac {1} {2}} \ operatorname {erfc} {\ frac {x} {\ sqrt {2}}}. \ End {aligned}}}$

Inverzní z cp je známý jako normální funkcí kvantilu , nebo pravděpodobnostní funkce a může být vyjádřena z hlediska funkce inverzní chyby jako

${\ displaystyle \ operatorname {probit} (p) = \ Phi ^{-1} (p) = {\ sqrt {2}} \ operatorname {erf} ^{-1} (2p-1) =-{\ sqrt {2}} \ operatorname {erfc} ^{-1} (2p).}$

Standardní normální cdf se používá častěji v pravděpodobnosti a statistice a chybová funkce se používá častěji v jiných odvětvích matematiky.

Chybová funkce je zvláštním případem funkce Mittag-Leffler a může být také vyjádřena jako splývající hypergeometrická funkce (Kummerova funkce):

${\ displaystyle \ operatorname {erf} x = {\ frac {2x} {\ sqrt {\ pi}}} M \ left ({\ tfrac {1} {2}}, {\ tfrac {3} {2}} , -x^{2} \ vpravo).}$

Má jednoduchý výraz z hlediska Fresnelova integrálu .

Pokud jde o regulovanou gama funkci P a neúplnou gama funkci ,

${\ displaystyle \ operatorname {erf} x = \ operatorname {sgn} x \ cdot P \ left ({\ tfrac {1} {2}}, x^{2} \ right) = {\ frac {\ operatorname {sgn } x} {\ sqrt {\ pi}}} \ gamma \ left ({\ tfrac {1} {2}}, x^{2} \ right).}$

sgn x je znaková funkce .

Zobecněné chybové funkce

Někteří autoři diskutují o obecnějších funkcích:

${\ Displaystyle E_ {n} (x) = {\ frac {n!} {\ sqrt {\ pi}}} \ int _ {0}^{x} e^{-t^{n}} \, dt = {\ frac {n!} {\ sqrt {\ pi}}} \ sum _ {p = 0}^{\ infty} (-1)^{p} {\ frac {x^{np+1}} {(np+1) p!}}.}$

Pozoruhodné případy jsou:

• E ₀ ( x ) je přímka skrz počátek: E ₀ ( x ) =X/e √ π
• E ₂ ( x ) je chybová funkce, erf x .

Po rozdělení n ! , všechny E _n pro liché n vypadají navzájem podobně (ale ne identicky). Podobně E _n pro sudé n vypadá podobně (ale ne identicky) navzájem po jednoduchém dělení n ! . Všechny generalizované chybové funkce pro n > 0 vypadají na kladné straně x grafu podobně .

Tyto zobecněné funkce lze ekvivalentně vyjádřit pro x > 0 pomocí funkce gama a neúplné funkce gama :

${\ Displaystyle E_ {n} (x) = {\ frac {1} {\ sqrt {\ pi}}} \ Gamma (n) \ left (\ Gamma \ left ({\ frac {1} {n}} \ vpravo)-\ Gamma \ vlevo ({\ frac {1} {n}}, x^{n} \ vpravo) \ vpravo), \ qquad x> 0.}$

Můžeme tedy definovat chybovou funkci z hlediska neúplné funkce gama:

${\ displaystyle \ operatorname {erf} x = 1-{\ frac {1} {\ sqrt {\ pi}}} \ Gamma \ left ({\ tfrac {1} {2}}, x^{2} \ right ).}$

Iterované integrály komplementární chybové funkce

Opakované integrály komplementární chybové funkce jsou definovány pomocí

${\ displaystyle {\ begin {aligned} \ operatorname {i} ^{n} \! \ operatorname {erfc} z & = \ int _ {z} ^{\ infty} \ operatorname {i} ^{n-1} \ ! \ operatorname {erfc} \ zeta \, d \ zeta \\ [6pt] \ operatorname {i} ^{0} \! \ operatorname {erfc} z & = \ operatorname {erfc} z \\\ operatorname {i} ^ {1} \! \ Operatorname {erfc} z & = \ operatorname {ierfc} z = {\ frac {1} {\ sqrt {\ pi}}} e^{-z^{2}}-z \ operatorname {erfc } z \\\ operatorname {i} ^{2} \! \ operatorname {erfc} z & = {\ tfrac {1} {4}} \ left (\ operatorname {erfc} z-2z \ operatorname {ierfc} z \ vpravo) \\\ end {aligned}}}$

Obecný vzorec pro opakování je

${\ Displaystyle 2n \ cdot \ operatorname {i} ^{n} \! \ operatorname {erfc} z = \ operatorname {i} ^{n-2} \! \ operatorname {erfc} z-2z \ cdot \ operatorname { i} ^{n-1} \! \ operatorname {erfc} z}$

Mají výkonovou řadu

${\ displaystyle \ operatorname {i}^{n} \! \ operatorname {erfc} z = \ sum _ {j = 0}^{\ infty} {\ frac {(-z)^{j}} {2^ {nj} j! \, \ Gamma \ left (1+{\ frac {nj} {2}} \ right)}},}$

ze kterého vyplývají vlastnosti symetrie

${\ displaystyle \ operatorname {i} ^{2m} \! \ operatorname {erfc} (-z) =-\ operatorname {i} ^{2m} \! \ operatorname {erfc} z+\ sum _ {q = 0} ^{m} {\ frac {z^{2q}} {2^{2 (mq) -1} (2q)! (mq)!}}}$

a

${\ displaystyle \ operatorname {i} ^{2m+1} \! \ operatorname {erfc} (-z) = \ operatorname {i} ^{2m+1} \! \ operatorname {erfc} z+\ sum _ {q = 0}^{m} {\ frac {z^{2q+1}} {2^{2 (mq) -1} (2q+1)! (Mq)!}}.}$

Implementace

Jako skutečná funkce skutečného argumentu

• V Posixových -kompatibilní operačních systémech, hlavička math.h prohlásí a matematická knihovna libm poskytne funkce erfa erfc( double přesnost ), stejně jako jejich jediný přesnost a rozšířené přesné protějšky erff, erfla erfcf, erfcl.
• GNU vědecká knihovna poskytuje erf, erfc, log(erf)a změnit jeho velikost chybová funkce.

Jako komplexní funkce komplexního argumentu

• libcerf , numerická C knihovna pro komplexní chybových funkcí, poskytuje komplexní funkcecerf,cerfc,cerfcxa skutečné funkceerfi,erfcxs přibližně 13 až 14 číslic přesnosti, založené na funkci Faddeeva jako implementována v MIT Faddeeva balíčku

Viz také

Související funkce

• Gaussův integrál , přes celou skutečnou linii
• Gaussova funkce , derivace
• Dawsonova funkce , renormalizovaná imaginární chybová funkce
• Goodwin – Staton integrál

V pravděpodobnosti

• Normální distribuce
• Normální kumulativní distribuční funkce , škálovaná a posunutá forma chybové funkce
• Probit , inverzní nebo kvantilní funkce normálního CDF
• Q-funkce , ocasní pravděpodobnost normálního rozdělení

Reference

Další čtení

• Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [červen 1964]. „Kapitola 7“ . Příručka matematických funkcí se vzorci, grafy a matematickými tabulkami . Řada aplikované matematiky. 55 (Devátý dotisk s dalšími opravami desátého originálního tisku s opravami (prosinec 1972); první vydání). Washington DC; New York: Ministerstvo obchodu USA, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN  64-60036 . MR  0167642 . LCCN  65-12253 .
• Press, William H .; Teukolsky, Saul A .; Vetterling, William T .; Flannery, Brian P. (2007), „Část 6.2. Neúplná funkce gama a chybová funkce“ , Numerical Recipes: The Art of Scientific Computing (3. vyd.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
• Temme, Nico M. (2010), „Error Functions, Dawson's and Fresnel Integrals“ , v Olver, Frank WJ ; Lozier, Daniel M .; Boisvert, Ronald F .; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions , Cambridge University Press, ISBN 978-0-521-19225-5, MR  2723248

externí odkazy

• MathWorld - Erf
• Tabulka integrálů chybových funkcí