Tečný prostor - Tangent space

V matematiky je tečný prostor z několika připojovacích zevšeobecní k vyšším rozměrům pojem tečnými rovinami na povrchy ve třech rozměrech a tečen na křivky ve dvou rozměrech. V kontextu fyziky lze na dotykový prostor k potrubí v určitém bodě pohlížet jako na prostor možných rychlostí pro částici pohybující se po potrubí.

Neformální popis

Obrazové znázornění tečného prostoru jednoho bodu na kouli . Vektor v tomto tangentovém prostoru představuje možnou rychlost at . Poté, co se tímto směrem přesuneme do blízkého bodu, rychlost by pak byla dána vektorem v tečném prostoru toho bodu - jiný tečný prostor, který není zobrazen.${\ displaystyle x}$${\ displaystyle x}$

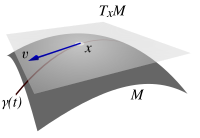
V diferenciální geometrii , je možné připojit ke každému bodu jednoho diferencovatelný potrubí je tečný prostor -a reálném vektorovém prostoru , který intuitivně obsahuje možné směry, ve kterých se dá tečně procházejí . Prvkům tečného prostoru v se říká tečné vektory v . Toto je zobecnění pojmu vektoru založeného na daném počátečním bodě v euklidovském prostoru . Rozměru tangenty prostoru na každém místě na připojené potrubí je stejný jako u potrubí samotného. ${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$

Například pokud je daným rozdělením koule - koule , pak si lze dotykový prostor v bodě představit jako rovinu, která se v tomto bodě dotýká koule a je kolmá na poloměr koule bodem. Obecněji řečeno, je-li daná potrubí je myšlenka jako vložený submanifold o Euclidean prostoru , pak může obraz tečný prostor v tomto doslovném způsobem. To byl tradiční přístup k definování paralelní dopravy . Mnoho autorů v diferenciální geometrii a obecné relativitě to používá. Přesněji, toto definuje afinní tečný prostor, který je odlišný od prostoru tečných vektorů popsaných moderní terminologií. ${\ displaystyle 2}$

V algebraické geometrii , v kontrastu, tam je vnitřní definice tangenty prostoru v místě, ze k algebraické rozmanitosti , která dává vektorový prostor o rozměrech alespoň to samo o sobě. Body, ve kterých je rozměr tečného prostoru přesně takový, jako body, se nazývají nejednotné body; ostatním se říká singulární body. Například křivka, která se kříží, nemá v daném bodě jedinečnou tečnou čáru. Jedinečné body jsou ty, kde selže „test být rozmanitým“. Viz tangenciální prostor Zariski . ${\ displaystyle V}$${\ displaystyle V}$${\ displaystyle p}$${\ displaystyle V}$${\ displaystyle V}$

Jakmile byly zavedeny tečné prostory potrubí, lze definovat vektorová pole , což jsou abstrakce rychlostního pole částic pohybujících se v prostoru. Vektorové pole připojí ke každému bodu potrubí vektor z tečného prostoru v tomto bodě hladkým způsobem. Takovéto vektorové pole slouží k definování zobecněné obyčejné diferenciální rovnice na potrubí: Řešením takové diferenciální rovnice je diferencovatelná křivka na potrubí, jejíž derivace v kterémkoli bodě je rovna vektoru tangenty připojenému k tomuto bodu vektorovým polem.

Všechny tečné prostory potrubí mohou být „slepeny k sobě“, aby vytvořily nové diferencovatelné potrubí s dvojnásobným rozměrem původního potrubí, nazývané tangentový svazek potrubí.

Formální definice

Výše uvedený neformální popis spoléhá na schopnost potrubí být vloženo do okolního vektorového prostoru, takže tečné vektory mohou „trčet“ z potrubí do okolního prostoru. Je však pohodlnější definovat pojem tečný prostor založený pouze na samotném potrubí. ${\ Displaystyle \ mathbb {R} ^{m}}$

Existují různé ekvivalentní způsoby definování tečných prostorů potrubí. Zatímco definice pomocí rychlosti křivek je intuitivně nejjednodušší, práce s ní je také nejtěžší. Elegantnější a abstraktní přístupy jsou popsány níže.

Definice pomocí tangentových křivek

Ve vloženém-potrubí obrázku, tečna vektor v místě je myšlenka jako rychlost části křivky procházející bodem . Můžeme tedy definovat tečný vektor jako třídu ekvivalence křivek, které procházejí, zatímco jsou navzájem tangenty v . ${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$

Předpokládejme, že je to diferencovatelné potrubí (s hladkostí ) a to . Vyberte si souřadnicový diagram , kde je otevřená podmnožina z obsahující . Předpokládejme dále, že jsou dány dvě křivky s tak, že obě jsou diferencovatelné v běžném smyslu (tyto diferencovatelné křivky nazýváme inicializované v ). Pak a se říká, že ekvivalentní v případě, a to pouze v případě, že deriváty a při splývají. To definuje vztah rovnocennosti na množině všech diferencovatelných křivek inicializována na , a třídy ekvivalence těchto křivek jsou známé jako tečnými vektory z na . Třída ekvivalence každé takové křivky je označena . Tečna prostor o u , označován , je potom definována jako množina všech tečných vektorů v ; nezávisí to na volbě souřadnicového grafu . ${\ displaystyle M}$${\ displaystyle C^{k}}$ ${\ Displaystyle k \ geq 1}$${\ displaystyle x \ v M}$ ${\ Displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$${\ displaystyle U}$${\ displaystyle M}$${\ displaystyle x}$${\ Displaystyle \ gamma _ {1}, \ gamma _ {2}: (-1,1) \ do M}$${\ displaystyle {\ gamma _ {1}} (0) = x = {\ gamma _ {2}} (0)}$${\ Displaystyle \ varphi \ circ \ gamma _ {1}, \ varphi \ circ \ gamma _ {2}: (-1,1) \ to \ mathbb {R} ^{n}}$${\ displaystyle x}$${\ displaystyle \ gamma _ {1}}$${\ displaystyle \ gamma _ {2}}$${\ displaystyle 0}$${\ Displaystyle \ varphi \ circ \ gamma _ {1}}$${\ Displaystyle \ varphi \ circ \ gamma _ {2}}$${\ displaystyle 0}$${\ displaystyle x}$${\ displaystyle M}$${\ displaystyle x}$${\ displaystyle \ gamma}$${\ displaystyle \ gamma '(0)}$${\ displaystyle M}$${\ displaystyle x}$${\ displaystyle T_ {x} M}$${\ displaystyle x}$${\ Displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$

Tečný prostor a tečný vektor podél křivky procházející skrz .${\ displaystyle T_ {x} M}$${\ displaystyle v \ v T_ {x} M}$${\ displaystyle x \ v M}$

Chcete-li definovat vektorový prostor operace , použijeme tabulku a definování mapy od kdy . Opět je třeba zkontrolovat, zda tato konstrukce nezávisí na konkrétním grafu a použité křivce , a ve skutečnosti to není. ${\ displaystyle T_ {x} M}$${\ Displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$ ${\ Displaystyle \ mathrm {d} {\ varphi} _ {x}: T_ {x} M \ to \ mathbb {R} ^{n}}$${\ Displaystyle {\ mathrm {d} {\ varphi} _ {x}} (\ gamma '(0)) \ mathrel {\ stackrel {\ text {df}} {=}} \ left. {\ frac {\ mathrm {d}} {\ mathrm {d} {t}}} [(\ varphi \ circ \ gamma) (t)] \ right | _ {t = 0},}$${\ displaystyle \ gamma \ in \ gamma '(0)}$${\ Displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$${\ displaystyle \ gamma}$

Mapa se vyklube bijective a mohou být použity pro přenos vektorový prostor operace na více než na , čímž se otočil druhou sadu do -rozměrného reálném vektorovém prostoru. ${\ displaystyle \ mathrm {d} {\ varphi} _ {x}}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle T_ {x} M}$${\ displaystyle n}$

Definice pomocí derivací

Předpokládejme nyní, že je to rozmanité. Říká se, že funkce se skutečnou hodnotou patří právě tehdy, když je pro každou souřadnicovou mapu mapa nekonečně odlišitelná. Všimněte si, že jde o skutečnou asociativní algebru s ohledem na bodový součin a součet funkcí a skalární násobení. ${\ displaystyle M}$${\ displaystyle C^{\ infty}}$${\ Displaystyle f: M \ to \ mathbb {R}}$${\ displaystyle {C^{\ infty}} (M)}$${\ Displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$${\ Displaystyle f \ circ \ varphi ^{-1}: \ varphi [U] \ subseteq \ mathbb {R} ^{n} \ to \ mathbb {R}}$${\ displaystyle {C^{\ infty}} (M)}$

Vyberte bod . Původ v je definována jako lineární mapa , která splňuje výše Leibniz identity ${\ displaystyle x \ v M}$${\ displaystyle x}$ ${\ Displaystyle D: {C^{\ infty}} (M) \ to \ mathbb {R}}$

${\ Displaystyle \ forall f, g \ in {C^{\ infty}} (M): \ qquad D (fg) = D (f) \ cdot g (x)+f (x) \ cdot D (g) ,}$

který je modelován podle součinového pravidla počtu.

(Z toho vyplývá, že pro každou stejně konstantní funkci ). ${\ displaystyle f = {\ text {const}},}$${\ displaystyle D (f) = 0}$

Pokud definujeme sčítání a skalární násobení na množině derivací v o ${\ displaystyle x}$

• ${\ Displaystyle (D_ {1}+D_ {2}) (f) \ mathrel {\ stackrel {\ text {df}} {=}} {D} _ {1} (f)+{D} _ {2 }(F)}$ a
• ${\ Displaystyle (\ lambda \ cdot D) (f) \ mathrel {\ stackrel {\ text {df}} {=}} \ lambda \ cdot D (f)}$,

pak získáme reálný vektorový prostor, které definujeme jako tečného prostoru o u . ${\ displaystyle T_ {x} M}$${\ displaystyle M}$${\ displaystyle x}$

Zobecnění

Zobecnění této definice je možné například u komplexních variet a algebraických odrůd . Člověk však místo zkoumání derivací z úplné algebry funkcí musí místo toho pracovat na úrovni zárodků funkcí. Důvodem pro to je, že se struktura svazek nemusí být v pořádku pro takové struktury. Například nechme být algebraickou odrůdou se strukturním svazkem . Pak Zariski tečný prostor v místě je sbírka všech -derivations , kde je půda pole a je stonek o u . ${\ displaystyle D}$${\ displaystyle X}$ ${\ displaystyle {\ mathcal {O}} _ {X}}$${\ displaystyle p \ v X}$${\ displaystyle \ mathbb {k}}$${\ Displaystyle D: {\ mathcal {O}} _ {X, p} \ to \ mathbb {k}}$${\ displaystyle \ mathbb {k}}$${\ displaystyle {\ mathcal {O}} _ {X, p}}$${\ displaystyle {\ mathcal {O}} _ {X}}$${\ displaystyle p}$

Rovnocennost definic

For a diferencovatelná křivka , která definuje (kde derivát je brán v běžném smyslu, protože je funkcí od do ). Lze zjistit, že jde o derivaci v bodě a že ekvivalentní křivky poskytují stejnou derivaci. Pro třídu ekvivalence tedy můžeme definovat, kde byla křivka zvolena libovolně. Mapa je vektorový prostorový izomorfismus mezi prostorem tříd ekvivalence a derivacemi v bodě${\ displaystyle x \ v M}$${\ Displaystyle \ gamma: (-1,1) \ do M}$${\ displaystyle \ gamma (0) = x,}$${\ displaystyle {D _ {\ gamma}} (f) \ mathrel {\ stackrel {\ text {df}} {=}} (f \ circ \ gamma) '(0)}$${\ displaystyle f \ circ \ gamma}$${\ Displaystyle (-1,1)}$${\ displaystyle \ mathbb {R}}$${\ displaystyle D _ {\ gamma} (f)}$${\ displaystyle x,}$${\ displaystyle \ gamma '(0),}$${\ Displaystyle {D _ {\ gamma '(0)}} (f) \ mathrel {\ stackrel {\ text {df}} {=}} (f \ circ \ gamma)' (0),}$${\ displaystyle \ gamma \ in \ gamma '(0)}$${\ displaystyle \ gamma '(0) \ mapsto D _ {\ gamma' (0)}}$${\ displaystyle \ gamma '(0)}$${\ displaystyle x.}$

Definice pomocí kotangensových prostorů

Znovu začínáme potrubím a bodem . Vezměme si ideál of která se skládá ze všech hladkých funkcí mizejících na , tj . Pak a jsou oba skutečné vektorové prostory, a kvocient prostor může být prokázáno, že isomorphic k cotangent prostoru prostřednictvím využití Taylorova věta . Tangenta prostor pak může být definováno jako duální prostor části . ${\ displaystyle C^{\ infty}}$${\ displaystyle M}$${\ displaystyle x \ v M}$ ${\ displaystyle I}$${\ displaystyle C^{\ infty} (M)}$${\ displaystyle f}$${\ displaystyle x}$${\ displaystyle f (x) = 0}$${\ displaystyle I}$${\ displaystyle I^{2}}$ ${\ displaystyle I/I^{2}}$ ${\ displaystyle T_ {x}^{*} M}$${\ displaystyle T_ {x} M}$${\ displaystyle I/I^{2}}$

I když je tato definice nejabstraktnější, je také tou, kterou lze nejsnáze přenést do jiných nastavení, například do variet uvažovaných v algebraické geometrii .

If is a derivation at , then for every , which means that makes rise to a linear map . Naopak, pokud je lineární mapa, pak definuje odvození na . Tím se získá ekvivalence mezi tečnými prostory definovanými derivacemi a tečnými prostory definovanými prostřednictvím kotangensových prostorů. ${\ displaystyle D}$${\ displaystyle x}$${\ displaystyle D (f) = 0}$${\ displaystyle f \ v I^{2}}$${\ displaystyle D}$${\ Displaystyle I/I^{2} \ to \ mathbb {R}}$${\ Displaystyle r: I/I^{2} \ to \ mathbb {R}}$${\ Displaystyle D (f) \ mathrel {\ stackrel {\ text {def}} {=}} r \ left ((ff (x))+I^{2} \ right)}$${\ displaystyle x}$

Vlastnosti

Pokud je otevřená podmnožina , pak je rozmanitým přirozeným způsobem (vezměte souřadnicové grafy jako mapy identity v otevřených podmnožinách ) a tečné prostory jsou přirozeně identifikovány s . ${\ displaystyle M}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle M}$${\ displaystyle C^{\ infty}}$${\ displaystyle \ mathbb {R} ^{n}}$${\ displaystyle \ mathbb {R} ^{n}}$

Tečné vektory jako směrové deriváty

Dalším způsobem, jak uvažovat o tangentových vektorech, jsou směrové deriváty . Vzhledem k tomu, že vektor je v , definuje odpovídající směrovou derivaci v bodě o ${\ displaystyle v}$${\ displaystyle \ mathbb {R} ^{n}}$${\ Displaystyle x \ in \ mathbb {R} ^{n}}$

${\ Displaystyle \ forall f \ in {C ^{\ infty}} (\ mathbb {R} ^{n}): \ qquad (D_ {v} f) (x) \ mathrel {\ stackrel {\ text {df }} {=}} \ left. {\ frac {\ mathrm {d}} {\ mathrm {d} {t}}} [f (x+tv)] \ right | _ {t = 0} = \ sum _ {i = 1}^{n} v^{i} {\ frac {\ částečný f} {\ částečný x^{i}}} (x).}$

Tato mapa je přirozeně odvozením na . Kromě toho má každá derivace v určitém bodě tuto formu. Mezi vektory (myšlenými jako tečné vektory v bodě) a derivacemi v bodě tedy existuje vzájemná korespondence. ${\ displaystyle x}$${\ displaystyle \ mathbb {R} ^{n}}$

Protože tečné vektory k obecnému potrubí v určitém bodě lze definovat jako derivace v tomto bodě, je přirozené je považovat za směrové deriváty. Konkrétně, pokud je tečný vektor se v bodě (představit jako derivace), pak platí směrovou derivaci ve směru od ${\ displaystyle v}$${\ displaystyle M}$${\ displaystyle x}$${\ displaystyle D_ {v}}$${\ displaystyle v}$

${\ Displaystyle \ forall f \ in {C^{\ infty}} (M): \ qquad {D_ {v}} (f) \ mathrel {\ stackrel {\ text {df}} {=}} v (f ).}$

Pokud uvažujeme jako počáteční rychlost diferencovatelné křivky inicializované na , tj. , Pak místo toho definujte pomocí ${\ displaystyle v}$${\ displaystyle \ gamma}$${\ displaystyle x}$${\ displaystyle v = \ gamma '(0)}$${\ displaystyle D_ {v}}$

${\ Displaystyle \ forall f \ in {C^{\ infty}} (M): \ qquad {D_ {v}} (f) \ mathrel {\ stackrel {\ text {df}} {=}} (f \ circ \ gamma) '(0).}$

Základ tečného prostoru v bodě

Pro potrubí , je-li graf je uveden s , pak lze definovat uspořádanou základnu z aplikace ${\ displaystyle C^{\ infty}}$${\ displaystyle M}$${\ Displaystyle \ varphi = (x^{1}, \ ldots, x^{n}): U \ to \ mathbb {R}^{n}}$${\ displaystyle p \ v U}$${\ Displaystyle \ left \ {\ left ({\ frac {\ partial} {\ partial x^{1}}} \ right) _ {p}, \ dots, \ left ({\ frac {\ partial} {\ částečné x^{n}}} \ vpravo) _ {p} \ vpravo \}}$${\ displaystyle T_ {p} M}$

${\ Displaystyle \ forall i \ in \ {1, \ ldots, n \}, ~ \ forall f \ in {C^{\ infty}} (M): \ qquad {\ left ({\ frac {\ partial} {\ partial x^{i}}} \ right) _ {p}} (f) \ mathrel {\ stackrel {\ text {df}} {=}} \ left ({\ frac {\ partial} {\ částečné x ^{i}}} {\ Big (} f \ circ \ varphi ^{-1} {\ Big)} \ right) {\ Big (} \ varphi (p) {\ Big)}.}$

Pak pro každý tečný vektor jeden má ${\ displaystyle v \ v T_ {p} M}$

${\ Displaystyle v = \ sum _ {i = 1}^{n} v^{i} \ cdot \ left ({\ frac {\ partial} {\ partial x^{i}}} \ right) _ {p }.}$

Tento vzorec je tedy vyjádřen jako lineární kombinace základních tečných vektorů definovaných souřadnicovým grafem . ${\ displaystyle v}$${\ Displaystyle \ left ({\ frac {\ partial} {\ partial x^{i}}} \ right) _ {p} \ in T_ {p} M}$${\ Displaystyle \ varphi: U \ to \ mathbb {R} ^{n}}$

Derivát mapy

Každá hladká (nebo diferencovatelná) mapa mezi hladkými (nebo diferencovatelnými) varietami indukuje přirozené lineární mapy mezi jejich odpovídajícími tečnými prostory: ${\ Displaystyle \ varphi: M \ až N}$

${\ Displaystyle \ mathrm {d} {\ varphi} _ {x}: T_ {x} M \ to T _ {\ varphi (x)} N.}$

Pokud je tečný prostor definován pomocí diferencovatelných křivek, pak je tato mapa definována pomocí

${\ Displaystyle {\ mathrm {d} {\ varphi} _ {x}} (\ gamma '(0)) \ mathrel {\ stackrel {\ text {df}} {=}} (\ varphi \ circ \ gamma) '(0).}$

Pokud je místo toho tečný prostor definován derivacemi, pak je tato mapa definována pomocí

${\ Displaystyle [\ mathrm {d} {\ varphi} _ {x} (D)] (f) \ mathrel {\ stackrel {\ text {df}} {=}} D (f \ circ \ varphi).}$

Lineární mapa je nazýván různě derivát , celkový derivace , diferenciál , nebo pushforward z na . Často se vyjadřuje pomocí řady dalších notací: ${\ displaystyle \ mathrm {d} {\ varphi} _ {x}}$${\ Displaystyle \ varphi}$${\ displaystyle x}$

${\ Displaystyle D \ varphi _ {x}, \ qquad (\ varphi _ {*}) _ {x}, \ qquad \ varphi '(x).}$

V jistém smyslu je derivát nejlepší lineární aproximací blízko . Všimněte si, že když , pak se mapa shoduje s obvyklým pojmem diferenci funkce . V místních souřadnicích je derivace dána jakobiánem . ${\ Displaystyle \ varphi}$${\ displaystyle x}$${\ Displaystyle N = \ mathbb {R}}$${\ Displaystyle \ mathrm {d} {\ varphi} _ {x}: T_ {x} M \ to \ mathbb {R}}$${\ Displaystyle \ varphi}$${\ Displaystyle \ varphi}$

Důležitý výsledek týkající se derivační mapy je následující:

Věta . Pokud je místní difeomorfismus na in , pak je lineární izomorfismus . Naopak, pokud je nepřetržitě differentiable a je izomorfismus, pak je tu otevřená sousedství z taková, že mapuje diffeomorphically na jeho obraze.${\ Displaystyle \ varphi: M \ až N}$${\ displaystyle x}$${\ displaystyle M}$${\ Displaystyle \ mathrm {d} {\ varphi} _ {x}: T_ {x} M \ to T _ {\ varphi (x)} N}$${\ Displaystyle \ varphi: M \ až N}$${\ displaystyle \ mathrm {d} {\ varphi} _ {x}}$ ${\ displaystyle U}$${\ displaystyle x}$${\ Displaystyle \ varphi}$${\ displaystyle U}$

Toto je zobecnění věty o inverzních funkcích na mapy mezi varietami.

Viz také

• Souřadnicový základ
• Kotangentní prostor
• Diferenciální geometrie křivek
• Exponenciální mapa
• Vektorový prostor

Poznámky

Reference

• Lee, Jeffrey M. (2009), Manifolds and Differential Geometry , Graduate Studies in Mathematics , 107 , Providence: American Mathematical Society.
• Michor, Peter W. (2008), Topics in Differential Geometry , Graduate Studies in Mathematics, 93 , Providence: American Mathematical Society.
• Spivak, Michael (1965), Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus , WA Benjamin, Inc., ISBN 978-0-8053-9021-6.

externí odkazy

• Tečná letadla v MathWorld