Hubený trojúhelník - Skinny triangle

V trigonometrie , je hubený trojúhelník je trojúhelník , jehož výška je podstatně větší než jeho základny. Řešení těchto trojúhelníků může být značně zjednodušena pomocí aproximace, že sinus malého úhlu se rovná úhlu v radiánech . Řešení je obzvláště jednoduché pro úzké trojúhelníky, které jsou také rovnoramennými nebo pravoúhlými trojúhelníky : v těchto případech lze zcela vynechat potřebu trigonometrických funkcí nebo tabulek .

Hubený trojúhelník nalezne využití v geodézii, astronomii a střelbě.

Rovnoramenný trojúhelník

Tabulka sinusových malých aproximačních chyb

Velké úhly	Malé úhly
úhel chyba (stupně) (radiány) (%) 1 0,017 0,005 2 0,035 0,02 5 0,087 0,13 10 0,175 0,51 15 0,262 1.15 20 0,349 2.06 25 0,436 3.25 30 0,524 4,72 35 0,611 6,50 40 0,698 8,61 45 0,785 11.07 50 0,873 13,92 55 0,960 17,19 60 1,047 20,92	úhel chyba (minut) (radiány) ( ppm ) 1 0,0003 0,01 2 0,0006 0,06 5 0,0015 0,35 10 0,0029 1.41 15 0,0044 3.17 20 0,0058 5,64 25 0,0073 8,81 30 0,0087 12,69 35 0,0102 17,28 40 0,0116 22.56 45 0,0131 28,56 50 0,0145 35,26 55 0,0160 42,66 60 0,0175 50,77

Přibližné řešení hubeného rovnoramenného trojúhelníku s odkazem na obrázek 1 je:

${\ Displaystyle b \ přibližně r \ theta \,}$

${\ displaystyle {\ text {area}} \ přibližně {\ frac {1} {2}} \ theta r ^ {2} \,}$

Toto je založeno na aproximacích malého úhlu :

${\ Displaystyle \ sin \ theta \ přibližně \ theta, \ quad \ theta \ ll 1 \,}$

a

${\ displaystyle \ cos \ theta = \ sin \ left ({\ frac {\ pi} {2}} - \ theta \ right) \ cca 1, \ quad \ theta \ ll 1}$

když je v radiánech . ${\ displaystyle \ scriptstyle \ theta}$

Důkaz řešení hubeného trojúhelníku vyplývá z aproximace malého úhlu použitím zákona sinusů . Opět s odkazem na obrázek 1:

${\ displaystyle {\ frac {b} {\ sin \ theta}} = {\ frac {r} {\ sin \ left ({\ frac {\ pi - \ theta} {2}} \ right)}}}$

Termín představuje základní úhel trojúhelníku a je touto hodnotou, protože součet vnitřních úhlů libovolného trojúhelníku (v tomto případě dva základní úhly plus θ ) se rovná π. Aplikace aproximace malého úhlu na zákon sinusů výše má za následek ${\ displaystyle \ scriptstyle {\ frac {\ pi - \ theta} {2}}}$

${\ displaystyle {\ frac {b} {\ theta}} \ přibližně {\ frac {r} {1}}}$

což je požadovaný výsledek.

Tento výsledek je ekvivalentní předpokladu, že délka základny trojúhelníku se rovná délce oblouku kruhu o poloměru r pod úhlem θ . Chyba je 10% nebo méně pro úhly menší než přibližně 43 ° a kvadraticky se zlepšuje: když se úhel zmenší o faktor k , chyba se sníží o k ² .

Bočního úhlu straně vzorec pro oblast trojúhelníku je

${\ displaystyle {\ text {area}} = {\ frac {\ sin \ theta} {2}} r ^ {2}}$

Výsledkem použití aproximace malého úhlu je

${\ displaystyle {\ text {area}} \ přibližně {\ frac {1} {2}} \ theta r ^ {2} \,}$

Pravoúhlý trojuhelník

Tabulka tečných malých aproximačních chyb

Velké úhly	Malé úhly
úhel chyba (stupně) (radiány) (%) 1 0,017 -0,01 5 0,087 -0,25 10 0,175 -1,02 15 0,262 -2,30 20 0,349 -4,09 25 0,436 -6,43 30 0,524 -9,31 35 0,611 -12,76 40 0,698 -16,80 45 0,785 -21,46 50 0,873 -26,77 55 0,960 -32,78 60 1,047 -39,54	úhel chyba (minut) (radiány) (ppm) 1 0,0003 -0,03 5 0,0015 -0,71 10 0,0029 -2,82 15 0,0044 -6,35 20 0,0058 -11,28 25 0,0073 -17,63 30 0,0087 -25,38 35 0,0102 -34,55 40 0,0116 -45,13 45 0,0131 -57,12 50 0,0145 -70,51 55 0,0160 -85,32 60 0,0175 -101,54

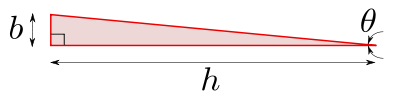
Přibližné řešení pravého hubeného trojúhelníku s odkazem na obrázek 3 je:

${\ displaystyle b \ přibližně h \ theta}$

Toto je založeno na aproximaci v malém úhlu

${\ Displaystyle \ tan \ theta \ přibližně \ theta, \ quad \ theta \ ll 1}$

který při nahrazení do přesného řešení

${\ displaystyle b = h \ tan \ theta \}$

přináší požadovaný výsledek.

Chyba této aproximace je menší než 10% pro úhly 31 ° nebo menší.

Aplikace

Aplikace hubeného trojúhelníku se vyskytují v každé situaci, kdy je třeba určit vzdálenost od vzdáleného objektu. K tomu může dojít při geodézii, astronomii a má to také vojenské aplikace.

Astronomie

Hubený trojúhelník se v astronomii často používá k měření vzdálenosti k objektům sluneční soustavy . Základna trojúhelníku je tvořena vzdáleností mezi dvěma měřicími stanicemi a úhel θ je úhel paralaxy tvořený objektem, jak je viděn těmito dvěma stanicemi. Tato základní linie je obvykle pro dosažení maximální přesnosti velmi dlouhá; v zásadě by stanice mohly být na opačných stranách Země . Tato vzdálenost je však stále krátká ve srovnání se vzdáleností k měřenému objektu (výška trojúhelníku) a lze použít řešení hubeného trojúhelníku a stále dosáhnout velké přesnosti. Alternativní metoda měření základních úhlů je teoreticky možná, ale není tak přesná. Základní úhly jsou téměř pravé úhly a pro dosažení stejné přesnosti by bylo nutné je měřit s mnohem větší přesností než úhel paralaxy.

Stejnou metodu měření úhlů paralaxy a použití hubeného trojúhelníku lze použít k měření vzdáleností ke hvězdám, alespoň k těm bližším. V případě hvězd je však obvykle vyžadována delší základní čára, než je průměr Země. Místo použití dvou stanic na základní linii se provádějí dvě měření ze stejné stanice v různých ročních obdobích. Během mezidobí se dráha Země kolem Slunce pohybuje měřicí stanicí na velkou vzdálenost, takže poskytuje velmi dlouhou základní linii. Tato základní linie může být dlouhá jako hlavní osa oběžné dráhy Země nebo ekvivalentně se dvěma astronomickými jednotkami (AU). Vzdálenost k hvězdě s úhlem paralaxy pouze jedné obloukové sekundy měřená na základní linii jedné AU je jednotka známá v astronomii jako parsec (pc) a rovná se přibližně 3,26 světelným rokům . Mezi vzdáleností v parsecích a úhlem v obloukových sekundách existuje inverzní vztah. Například dvě obloukové sekundy odpovídají vzdálenosti 0,5 pc a 0,5 obloukové sekundy odpovídá vzdálenosti dvou parseků.

Dělostřelba

Tenký trojúhelník je v dělostřelbě užitečný v tom, že umožňuje vypočítat vztah mezi rozsahem a velikostí cíle, aniž by střelec musel počítat nebo hledat nějaké trigonometrické funkce . Vojenské a lovecké teleskopické mířidla mají často záměrný kříž kalibrovaný na miliradiány , v této souvislosti se obvykle nazývá jen mils nebo mil-dots. Terč o výšce 1 metr a měření 1 mil v zorném poli odpovídá dosahu 1000 metrů. Mezi úhlem měřeným v pohledu odstřelovače a vzdáleností k cíli existuje inverzní vztah. Například pokud tentýž cíl měří 2 míle v zorném poli, pak je dosah 500 metrů.

Další jednotkou, která se někdy používá u zaměřovačů, je minuta oblouku (MOA). Vzdálenosti odpovídající minutám oblouku nejsou přesná čísla v metrickém systému, jako jsou u miliradiánů; existuje však pohodlná přibližná korespondence celého čísla v imperiálních jednotkách . Terč o výšce 1 palec a měřící 1 MOA v zorném poli odpovídá rozsahu 100 yardů . Nebo možná užitečněji cíl 6 stop na výšku a měření 4 MOA odpovídá rozsahu 1800 yardů (něco přes míli).

Letectví

Jednoduchá forma letecké navigace, mrtvé počítání , se spoléhá na to, že se při výpočtu požadovaného kurzu počítá s odhadem rychlosti větru na velké vzdálenosti. Vzhledem k tomu, že předpovězené nebo hlášené rychlosti větru jsou zřídka přesné, je třeba v pravidelných intervalech provádět korekce směru letu. Hubené trojúhelníky tvoří základ pravidla 1 ku 60 , což je „Po ujetí 60 mil je váš kurz o jeden stupeň nižší za každou míli, kterou jste mimo kurs“. „60“ je velmi blízko 180 / π = 57,30.

Viz také

• Infinitezimální oscilace kyvadla

Reference

Bibliografie

• George Ogden Abell, David Morrison, Sidney C. Wolff, Exploration of the Universe , Saunders College Pub., 1987 ISBN  0-03-005143-6 .
• Jim Breithaupt, Fyzika pro pokročilou úroveň , Nelson Thornes, 2000 ISBN  0-7487-4315-4 .
• Charles H. Holbrow, James N.Lloyd, Joseph C. Amato, Enrique Galvez, Beth Parks, Modern Introductory Physics , Springer, 2010 ISBN  0-387-79079-9 .
• Srini Vasan, Základy fotoniky a optiky , Trafford Publishing, 2004 ISBN  1-4120-4138-4 .
• Tom A. Warlow, Střelné zbraně, právo a forenzní balistika , Taylor & Francis, 1996 ISBN  0-7484-0432-5 .