Systém Hilbert - Hilbert system

V matematické fyzice je Hilbertův systém zřídka používaný termín pro fyzikální systém popsaný C*-algebrou .

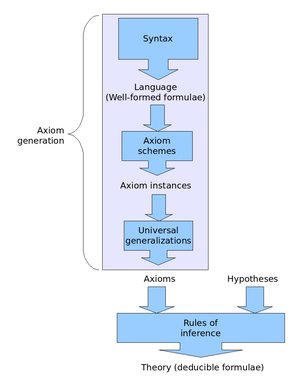
V logice , zejména matematické logice , je Hilbertův systém , někdy nazývaný také Hilbertův kalkul , deduktivní systém ve stylu Hilberta nebo systém Hilbert – Ackermann , typ systému formální dedukce přisuzovaný Gottlobovi Fregeovi a Davidu Hilbertovi . Tyto deduktivní systémy jsou nejčastěji studovány pro logiku prvního řádu , ale jsou zajímavé i pro další logiku.

Většina variant Hilbertových systémů má charakteristický nádech ve způsobu, jakým vyvažují kompromis mezi logickými axiomy a pravidly odvozování . Hilbertovy systémy lze charakterizovat volbou velkého počtu schémat logických axiomů a malého souboru pravidel odvozování . Systémy přirozené dedukce mají opačný směr, včetně mnoha pravidel pro odpočet, ale velmi málo nebo žádné schémata axiomu. Nejčastěji studované Hilbertovy systémy mají buď jen jedno pravidlo odvození - modus ponens , pro propoziční logiku  - nebo dvě - s generalizací , aby zvládly i predikátovou logiku - a několik nekonečných schémat axiomu. Hilbertovy systémy propoziční modální logiky , někdy nazývané Hilbert-Lewisovy systémy , jsou obecně axiomatizovány dvěma dalšími pravidly, pravidlem nutnosti a pravidlem jednotné substituce .

Charakteristickým rysem mnoha variant Hilbertových systémů je, že kontext se v žádném z jejich odvozovacích pravidel nemění, zatímco přirozená dedukce i sekvenční počet obsahují některá pravidla měnící kontext. Pokud se tedy někdo zajímá pouze o odvozitelnost tautologií , žádné hypotetické soudy, pak lze formalizovat Hilbertův systém tak, že jeho pravidla pro odvození obsahují pouze úsudky dosti jednoduché formy. Totéž nelze udělat s dalšími dvěma dedukčními systémy: jelikož se v některých jejich pravidlech pro závěry mění kontext, nemohou být formalizovány tak, aby se dalo vyhnout hypotetickým úsudkům - dokonce ani když je chceme použít jen pro prokázání derivovatelnosti tautologií .

Formální odpočty

V systému dedukce v Hilbertově stylu je formální dedukce konečná posloupnost vzorců, ve kterých je každý vzorec buď axiomem, nebo je získán z předchozích vzorců pravidlem odvození. Tyto formální dedukce mají zrcadlit důkazy v přirozeném jazyce, i když jsou mnohem podrobnější.

Předpokládejme, že je to soubor vzorců, považovaných za hypotézy . Může to být například sada axiomů pro teorii skupin nebo teorii množin . Zápis znamená, že existuje dedukce, která končí tím, že se jako axiomy použijí pouze logické axiomy a prvky . Neformálně to tedy znamená, že je to prokazatelné za předpokladu všech vzorců v . ${\ displaystyle \ Gamma}$${\ displaystyle \ Gamma}$${\ displaystyle \ Gamma \ vdash \ phi}$${\ displaystyle \ phi}$${\ displaystyle \ Gamma}$${\ displaystyle \ Gamma \ vdash \ phi}$${\ displaystyle \ phi}$${\ displaystyle \ Gamma}$

Odvozovací systémy ve stylu Hilberta se vyznačují použitím četných schémat logických axiomů . Schéma axiom je nekonečná množina axiómů získaných substitucí všechny vzorce nějaké formy do určitého vzoru. Sada logických axiomů zahrnuje nejen ty axiomy generované z tohoto vzoru, ale také jakékoli zobecnění jednoho z těchto axiomů. Zobecnění vzorce se získá předponou nula nebo více univerzálních kvantifikátorů ve vzorci; například je generalizace . ${\ Displaystyle \ forall y (\ forall xPxy \ to Pty)}$${\ displaystyle \ forall xPxy \ to Pty}$

Logické axiomy

Existuje několik variantních axiomatizací predikátové logiky, protože pro jakoukoli logiku existuje svoboda ve výběru axiomů a pravidel, která tuto logiku charakterizují. Popisujeme zde Hilbertův systém s devíti axiomy a jen pravidlem modus ponens, kterému říkáme jednopravová axiomatizace a který popisuje klasickou rovníkovou logiku. Zabýváme se minimální jazyk této logiky, kde formule používat pouze spojek a a pouze kvantifikátor . Později si ukážeme, jak lze systém rozšířit o další logické spojky, jako například a bez rozšíření třídy dedukovatelných vzorců. ${\ displaystyle \ lnot}$${\ displaystyle \ to}$${\ displaystyle \ forall}$${\ displaystyle \ land}$${\ displaystyle \ lor}$

První čtyři logická schémata axiomu umožňují (společně s modus ponens) manipulaci s logickými spojkami.

P1. ${\ displaystyle \ phi \ to \ phi}$

P2. ${\ displaystyle \ phi \ to \ left (\ psi \ to \ phi \ right)}$

P3. ${\ Displaystyle \ left (\ phi \ to \ left (\ psi \ rightarrow \ xi \ right) \ right) \ to \ left (\ left (\ phi \ to \ psi \ right) \ to \ left (\ phi \ na \ xi \ vpravo) \ vpravo)}$

P4. ${\ Displaystyle \ left (\ lnot \ phi \ to \ lnot \ psi \ right) \ to \ left (\ psi \ to \ phi \ right)}$

Axiom P1 je nadbytečný, jak vyplývá z P3, P2 a modus ponens (viz důkaz ). Tyto axiomy popisují klasickou výrokovou logiku ; bez axiomu P4 získáme pozitivní implikační logiku . Minimální logiky je dosaženo buď přidáním namísto axiomu P4m, nebo definováním jako . ${\ displaystyle \ lnot \ phi}$${\ displaystyle \ phi \ to \ bot}$

P4m. ${\ Displaystyle \ left (\ phi \ to \ psi \ right) \ to \ left (\ left (\ phi \ to \ lnot \ psi \ right) \ to \ lnot \ phi \ right)}$

Intuicionistické logiky je dosaženo přidáním axiomů P4i a P5i k pozitivní implikační logice nebo přidáním axiomu P5i k minimální logice. P4i i P5i jsou věty klasické výrokové logiky.

P4i. ${\ Displaystyle \ left (\ phi \ to \ lnot \ phi \ right) \ to \ lnot \ phi}$

P5i. ${\ Displaystyle \ lnot \ phi \ to \ left (\ phi \ to \ psi \ right)}$

Všimněte si, že se jedná o schémata axiomů, která představují nekonečně mnoho konkrétních případů axiomů. Například P1 může představovat konkrétní instanci axiomu nebo může představovat : je místo, kde lze umístit libovolný vzorec. Proměnná, jako je tato, která se pohybuje nad vzorci, se nazývá „schematická proměnná“. ${\ displaystyle p \ to p}$${\ Displaystyle \ left (p \ to q \ right) \ to \ left (p \ to q \ right)}$${\ displaystyle \ phi}$

S druhým pravidlem jednotné substituce (USA) můžeme změnit každé z těchto schémat axiomu na jeden axiom, přičemž každou schematickou proměnnou nahradíme nějakou propoziční proměnnou, která není uvedena v žádném axiomu, abychom získali to, čemu říkáme substituční axiomatizace. Obě formalizace mají proměnné, ale tam, kde jednopravidlová axiomatizace má schematické proměnné, které jsou mimo jazyk logiky, používá substituční axiomatizace výrokové proměnné, které dělají stejnou práci tím, že vyjadřují myšlenku proměnné pohybující se přes vzorce pomocí pravidla, které používá substituci.

NÁS. Nechť je vzorec s jednou nebo více instancemi výrokové proměnné a nechť je jiný vzorec. Pak od , usoudit .${\ Displaystyle \ phi (p)}$${\ displaystyle p}$${\ Displaystyle \ psi}$${\ Displaystyle \ phi (p)}$${\ Displaystyle \ phi (\ psi)}$

Další tři logická schémata axiomů poskytují způsoby, jak přidávat, manipulovat a odebírat univerzální kvantifikátory.

Q5. kde t může být nahrazeno x v${\ Displaystyle \ forall x \ left (\ phi \ right) \ to \ phi [x: = t]}$${\ displaystyle \, \! \ phi}$

Q6. ${\ Displaystyle \ forall x \ left (\ phi \ to \ psi \ right) \ to \ left (\ forall x \ left (\ phi \ right) \ to \ forall x \ left (\ psi \ right) \ right) }$

Q7. kde x není v .${\ Displaystyle \ phi \ to \ forall x \ left (\ phi \ right)}$${\ displaystyle \ phi}$

Tato tři další pravidla rozšiřují výrokový systém, aby axiomatizoval klasickou predikátovou logiku . Podobně tato tři pravidla rozšiřují systém pro intuitivní propoziční logiku (s P1-3 a P4i a P5i) na logiku prediktivní intuice .

Univerzální kvantifikace je často poskytována alternativní axiomatizace pomocí extra pravidla zobecnění (viz část Metatheorems), v takovém případě jsou pravidla Q6 a Q7 nadbytečná.

Konečná schémata axiomu jsou vyžadována pro práci se vzorci zahrnujícími symbol rovnosti.

I8. pro každou proměnnou x .${\ displaystyle x = x}$

I9. ${\ Displaystyle \ left (x = y \ right) \ to \ left (\ phi [z: = x] \ to \ phi [z: = y] \ right)}$

Konzervativní rozšíření

Je běžné zahrnout do systému dedukce ve stylu Hilberta pouze axiomy pro implikaci a negaci. Vzhledem k těmto axiómům je možné vytvořit konzervativní rozšíření věty o dedukci, které umožňují použití dalších spojek. Tato rozšíření se nazývají konzervativní, protože pokud je vzorec φ zahrnující nové spojky přepsán jako logicky ekvivalentní vzorec θ zahrnující pouze negaci, implikaci a univerzální kvantifikaci, pak φ je v rozšířeném systému odvozitelný právě tehdy, pokud je θ odvozitelný v původním systému . Po úplném rozšíření bude systém ve stylu Hilberta více připomínat systém přirozené dedukce .

Existenciální kvantifikace

• Úvod

${\ Displaystyle \ forall x (\ phi \ to \ existuje y (\ phi [x: = y]))}$

• Odstranění

${\ Displaystyle \ forall x (\ phi \ to \ psi) \ to \ existuje x (\ phi) \ to \ psi}$kde není volný proměnná z .${\ displaystyle x}$${\ Displaystyle \ psi}$

Spojení a rozpojení

• Úvod a odstranění spojky

úvod: ${\ Displaystyle \ alpha \ to \ beta \ to \ alpha \ land \ beta}$

zbývající eliminace: ${\ Displaystyle \ alpha \ wedge \ beta \ to \ alpha}$

eliminační právo: ${\ Displaystyle \ alpha \ wedge \ beta \ to \ beta}$

• Úvod a odstranění disjunkce

úvod vlevo: ${\ Displaystyle \ alpha \ to \ alpha \ vee \ beta}$

úvod vpravo: ${\ Displaystyle \ beta \ to \ alpha \ vee \ beta}$

odstranění: ${\ Displaystyle (\ alpha \ to \ gamma) \ to (\ beta \ to \ gamma) \ to \ alpha \ vee \ beta \ to \ gamma}$

Metatheoremy

Protože systémy ve stylu Hilberta mají velmi málo pravidel pro odpočet, je běžné prokázat metateorémy, které ukazují, že další pravidla pro odpočet nepřidávají žádnou deduktivní sílu, v tom smyslu, že odpočet pomocí nových pravidel pro odpočet lze převést na odpočet pouze pomocí původního odpočtu pravidla.

Některé běžné metateorémy této formy jsou:

• Věta o dedukci : tehdy a jen tehdy, jestliže .${\ Displaystyle \ Gamma; \ phi \ vdash \ psi}$${\ Displaystyle \ Gamma \ vdash \ phi \ to \ psi}$
• ${\ Displaystyle \ Gamma \ vdash \ phi \ leftrightarrow \ psi}$jestli a jen když a .${\ Displaystyle \ Gamma \ vdash \ phi \ to \ psi}$${\ Displaystyle \ Gamma \ vdash \ psi \ to \ phi}$
• Kontrapozice: Je-li poté .${\ Displaystyle \ Gamma; \ phi \ vdash \ psi}$${\ Displaystyle \ Gamma; \ lnot \ psi \ vdash \ lnot \ phi}$
• Zobecnění : Pokud a x se nevyskytuje volně v žádném vzorci pak .${\ displaystyle \ Gamma \ vdash \ phi}$${\ displaystyle \ Gamma}$${\ Displaystyle \ Gamma \ vdash \ forall x \ phi}$

Některé užitečné věty a jejich důkazy

Následuje několik vět v propoziční logice spolu s jejich důkazy (nebo odkazy na tyto důkazy v jiných článcích). Jelikož (P1) samotný lze dokázat pomocí ostatních axiomů, ve skutečnosti (P2), (P3) a (P4) stačí k prokázání všech těchto vět.

(HS1) - Hypotetický sylogismus , viz důkaz .${\ Displaystyle (q \ to r) \ to ((p \ to q) \ to (p \ to r))}$

(L1) - důkaz: ${\ Displaystyle p \ to ((p \ to q) \ to q)}$

(1)       (instance (P3))${\ Displaystyle ((p \ to q) \ to (p \ to q)) \ to (((p \ to q) \ to p) \ to ((p \ to q) \ to q))}$

(2)       (instance (P1))${\ Displaystyle (p \ to q) \ to (p \ to q)}$

(3)       (od (2) a (1) od modus ponens )${\ Displaystyle ((p \ to q) \ to p) \ to ((p \ to q) \ to q)}$

(4)       (instance (HS1))${\ Displaystyle ((((p \ to q) \ to p) \ to ((p \ to q) \ to q)) \ to ((p \ to ((p \ to q) \ to p)) \ k (p \ to ((p \ to q) \ to q)))}$

(5)       (from (3) and (4) by modus ponens)${\ Displaystyle (p \ to ((p \ to q) \ to p)) \ to (p \ to ((p \ to q) \ to q))}$

(6)       (instance (P2))${\ Displaystyle p \ to ((p \ to q) \ to p)}$

(7)       (from (6) and (5) by modus ponens)${\ Displaystyle p \ to ((p \ to q) \ to q)}$

Následující dvě věty jsou společně označovány jako dvojitá negace :

(DN1)${\ Displaystyle \ neg \ neg p \ to p}$

(DN2) ${\ Displaystyle p \ to \ neg \ neg p}$

Viz důkazy .

(L2) - pro tento důkaz používáme metodu hypotetického sylogismu metatheorem jako zkratku pro několik důkazních kroků: ${\ Displaystyle (p \ to (q \ to r)) \ to (q \ to (p \ to r))}$

(1)       (instance (P3))${\ Displaystyle (p \ to (q \ to r)) \ to ((p \ to q) \ to (p \ to r))}$

(2)       (instance (HS1))${\ Displaystyle ((p \ to q) \ to (p \ to r)) \ to ((q \ to (p \ to q)) \ to (q \ to (p \ to r)))}$

(3)       (from (1) and (2) using the hypotetical syllogism metatheorem)${\ Displaystyle (p \ to (q \ to r)) \ to ((q \ to (p \ to q)) \ to (q \ to (p \ to r)))}$

(4)       (instance (P3))${\ Displaystyle ((p \ to (q \ to r)) \ to ((q \ to (p \ to q)) \ to (q \ to (p \ to r)))) \ to (((p \ to (q \ to r)) \ to (q \ to (p \ to q))) \ to ((p \ to (q \ to r)) \ to (q \ to (p \ to r)) ))}$

(5)       (od (3) a (4) pomocí modus ponens)${\ Displaystyle ((p \ to (q \ to r)) \ to (q \ to (p \ to q))) \ to ((p \ to (q \ to r)) \ to (q \ to ( p \ až r)))}$

(6)       (instance (P2))${\ Displaystyle q \ to (p \ to q)}$

(7)       (instance (P2))${\ Displaystyle (q \ to (p \ to q)) \ to ((p \ to (q \ to r)) \ to (q \ to (p \ to q)))}$

(8)       (from (6) and (7) using modus ponens)${\ Displaystyle (p \ to (q \ to r)) \ to (q \ to (p \ to q))}$

(9)       (od (8) a (5) pomocí modus ponens)${\ Displaystyle (p \ to (q \ to r)) \ to (q \ to (p \ to r))}$

(HS2) - alternativní forma hypotetického sylogismu . důkaz: ${\ Displaystyle (p \ to q) \ to ((q \ to r) \ to (p \ to r))}$

(1)       (instance (HS1))${\ Displaystyle (q \ to r) \ to ((p \ to q) \ to (p \ to r))}$

(2)       (instance (L2))${\ Displaystyle ((q \ to r) \ to ((p \ to q) \ to (p \ to r))) \ to ((p \ to q) \ to ((q \ to r) \ to ( p \ až r)))}$

(3) (od (1) a (2) od modus ponens)${\ Displaystyle (p \ to q) \ to ((q \ to r) \ to (p \ to r))}$

(TR1) - Transpozice, viz důkaz (druhý směr transpozice je (P4)).${\ Displaystyle (p \ to q) \ to (\ neg q \ to \ neg p)}$

(TR2) - další forma transpozice; důkaz: ${\ Displaystyle (\ neg p \ to q) \ to (\ neg q \ to p)}$

(1)       (instance (TR1))${\ Displaystyle (\ neg p \ to q) \ to (\ neg q \ to \ neg \ neg p)}$

(2)       (instance (DN1))${\ Displaystyle \ neg \ neg p \ to p}$

(3)       (instance (HS1))${\ Displaystyle (\ neg \ neg p \ to p) \ to ((\ neg q \ to \ neg \ neg p) \ to (\ neg q \ to p))}$

(4)       (from (2) and (3) by modus ponens)${\ Displaystyle (\ neg q \ to \ neg \ neg p) \ to (\ neg q \ to p)}$

(5)       (from (1) and (4) using the hypotetical syllogism metatheorem)${\ Displaystyle (\ neg p \ to q) \ to (\ neg q \ to p)}$

(L3) - důkaz: ${\ Displaystyle (\ neg p \ to p) \ to p}$

(1)       (instance (P2))${\ Displaystyle \ neg p \ to (\ neg \ neg (q \ to q) \ to \ neg p)}$

(2)       (instance (P4))${\ Displaystyle (\ neg \ neg (q \ to q) \ to \ neg p) \ to (p \ to \ neg (q \ to q))}$

(3)       (from (1) and (2) using the hypotetical syllogism metatheorem)${\ Displaystyle \ neg p \ to (p \ to \ neg (q \ to q))}$

(4)       (instance (P3))${\ Displaystyle (\ neg p \ to (p \ to \ neg (q \ to q))) \ to ((\ \ neg p \ to p) \ to (\ neg p \ to \ neg (q \ to q) ))}$

(5)       (od (3) a (4) pomocí režimů ponens)${\ Displaystyle (\ neg p \ to p) \ to (\ neg p \ to \ neg (q \ to q))}$

(6)       (instance (P4))${\ Displaystyle (\ neg p \ to \ neg (q \ to q)) \ to ((q \ to q) \ to p)}$

(7)       (from (5) and (6) using the hypotetical syllogism metatheorem)${\ Displaystyle (\ neg p \ to p) \ to ((q \ to q) \ to p)}$

(8)       (instance (P1))${\ Displaystyle q \ to q}$

(9)       (instance (L1))${\ Displaystyle (q \ to q) \ to ((((q \ to q) \ to p) \ to p)}$

(10)       (od (8) a (9) pomocí režimů ponens)${\ displaystyle ((q \ to q) \ to p) \ to p}$

(11)       (from (7) and (10) using the hypotetical syllogism metatheorem)${\ Displaystyle (\ neg p \ to p) \ to p}$

Alternativní axiomatizace

Axiom 3 výše je připsán Łukasiewiczovi . Původní systém od Frege měl axiomy P2 a P3, ale čtyři další axiomy namísto axiomu P4 (viz Fregeův propoziční kalkul ). Russell a Whitehead také navrhli systém s pěti výrokovými axiomy.

Další spojení

Axiomy P1, P2 a P3, s pravidlem dedukce modus ponens (formalizující intuicionální výroková logika ), odpovídají kombinátorům kombinační logické báze I , K a S s operátorem aplikace. Důkazy v Hilbertově systému pak odpovídají kombinátorovým pojmům v kombinační logice. Viz také korespondence Curry -Howarda .

Viz také

• Seznam systémů Hilbert
• Přirozená dedukce

Poznámky

Reference

• Curry, Haskell B .; Robert Feys (1958). Combinatory Logic Vol. Já . 1 . Amsterdam: Severní Holandsko.
• Monk, J. Donald (1976). Matematická logika . Absolventské texty z matematiky. Berlín, New York: Springer-Verlag . ISBN 978-0-387-90170-1.CS1 maint: postscript ( odkaz )
• Ruzsa, Imre; Máté, András (1997). Bevezetés a moderní logikába (v maďarštině). Budapešť: Osiris Kiadó.
• Tarski, Alfred (1990). Bizonyítás és igazság (v maďarštině). Budapešť: Gondolat.Jedná se o maďarský překlad vybraných prací Alfreda Tarského o sémantické teorii pravdy .
• David Hilbert (1927) „Základy matematiky“, přeložili Stephan Bauer-Menglerberg a Dagfinn Føllesdal (s. 464–479). v:
  • van Heijenoort, Jean (1967). From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931 (3. tisk 1976 ed.). Cambridge MA: Harvard University Press. ISBN 0-674-32449-8.
  • Hilbertova 1927, Na základě dřívější přednášky o „základech“ z roku 1925 (s. 367–392), představuje jeho 17 axiomů-axiomy implikace #1-4, axiomy o & a V #5-10, axiomy negace #11- 12, jeho logický ε-axiom #13, axiomy rovnosti #14-15 a axiomy čísla #16-17-spolu s dalšími nezbytnými prvky jeho formalistické „teorie důkazu“-např. Indukční axiomy, rekurzivní axiomy, atd; nabízí také temperamentní obranu proti intuiciismu LEJE Brouwera. Viz také komentáře a vyvrácení Hermanna Weyla (1927) (s. 480–484), příloha Paula Bernaye (1927) k Hilbertově přednášce (s. 485–489) a odpověď Luitzena Egberta Jana Brouwera (1927) (s. 490–495)
• Kleene, Stephen Cole (1952). Úvod do metamatematiky (10. dojem s opravami z roku 1971 ed.). Amsterdam NY: North Holland Publishing Company. ISBN 0-7204-2103-9.
  • Viz zejména Kapitola IV Formální systém (str. 69–85), kde Kleene uvádí podkapitoly §16 Formální symboly, §17 Pravidla formace, §18 Volné a vázané proměnné (včetně substituce), §19 Transformační pravidla (např. Modus ponens) - a z nich uvádí 21 „postulátů“-18 axiomů a 3 vztahy „bezprostředních důsledků“ rozdělené následovně: Postuláty pro propoziční počet #1-8, Další postuláty pro predikátový počet #9-12 a Další postuláty pro teorie čísel #13-21.

externí odkazy

• Gaifman, Haim. „Odvodný systém typu Hilbert pro větnou logiku, úplnost a kompaktnost“ (pdf) .
• Farmář, WM „Propositional logic“ (pdf) .Popisuje (mimo jiné) část dedukčního systému ve stylu Hilberta (omezeno na propoziční kalkul ).