Stabilní distribuce - Stable distribution

Stabilní

Funkce hustoty pravděpodobnosti Symetrické α -stabilní distribuce s jednotkovým měřítkovým faktorem Zkosené středové stabilní rozdělení s jednotkovým měřítkovým faktorem
Kumulativní distribuční funkce CDF pro symetrické a -stabilní distribuce CDF pro šikmé středové stabilní distribuce
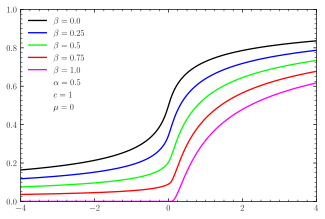
Parametry	α ∈ (0, 2] - parametr stability β ∈ [−1, 1] - parametr šikmosti (všimněte si, že šikmost není definována) c ∈ (0, ∞) - parametr měřítka μ ∈ (−∞, ∞) - parametr umístění
Podpěra, podpora	x ∈ [ μ , +∞), pokud α <1 a β = 1 x ∈ (-∞, μ ], pokud α <1 a β = −1 x ∈ R jinak
PDF	není analyticky vyjádřitelný, s výjimkou některých hodnot parametrů
CDF	není analyticky vyjádřitelný, s výjimkou určitých hodnot parametrů
Znamenat	μ při α > 1 , jinak nedefinováno
Medián	μ, když β = 0 , jinak není analyticky vyjádřen
Režim	μ, když β = 0 , jinak není analyticky vyjádřen
Variance	2 c 2 když α = 2 , jinak nekonečné
Šikma	0, když α = 2 , jinak nedefinováno
Př. kurtóza	0, když α = 2 , jinak nedefinováno
Entropie	není analyticky vyjádřitelný, s výjimkou určitých hodnot parametrů
MGF	${\ Displaystyle \ exp \! \ left (t \ mu +c^{2} t^{2} \ right)}$kdy , jinak nedefinováno${\ Displaystyle \ alpha = 2}$
CF	${\ Displaystyle \ exp \! {\ Big [} \; it \ mu -| c \, t |^{\ alpha} \, (1 -i \ beta \ operatorname {sgn} (t) \ Phi) \; {\ Big]},}$ kde ${\ Displaystyle \ Phi = {\ begin {cases} \ tan {\ tfrac {\ pi \ alpha} {2}} & {\ text {if}} \ alpha \ neq 1 \\-{\ tfrac {2} { \ pi}} \ log | c \, t | & {\ text {if}} \ alpha = 1 \ end {cases}}}$

V teorii pravděpodobnosti je rozdělení považováno za stabilní, pokud má lineární kombinace dvou nezávislých náhodných proměnných s tímto rozdělením stejné rozdělení, a to až do umístění a parametrů měřítka . Náhodná proměnná je prý stabilní, pokud je stabilní její rozdělení. Stabilní distribuční rodina je také někdy označována jako Alvy-stabilní distribuce Lévy , po Paulu Lévym , prvním matematikovi, který ji studoval.

Ze čtyř parametrů definujících rodinu byla největší pozornost zaměřena na parametr stability α (viz panel). Stabilní distribuce mají 0 < α ≤ 2 s tím, že horní hranice, která odpovídá normálnímu rozdělení , a α = 1 do Cauchy distribuce . Distribuce mají nedefinovaný rozptyl pro α <2 a nedefinovaný průměr pro α ≤ 1 . Důležitost stabilních rozdělení pravděpodobnosti spočívá v tom, že jsou „ atraktory “ pro správně normované součty nezávislých a identicky rozložených ( iid ) náhodných proměnných. Normální distribuce definuje rodinu stabilních distribucí. Podle klasické centrální limitní věty bude správně normovaný součet množiny náhodných proměnných, každá s konečným rozptylem, směřovat k normálnímu rozdělení, jak se počet proměnných zvyšuje. Bez předpokladu konečné odchylky může být limitem stabilní rozdělení, které není normální. Mandelbrot uvedené na takové rozdělení jako „stabilní Paretian distribucí“, po Vilfredo Pareto . Zejména označil ty, které byly maximálně vychýlené v kladném směru s 1 < α <2, za „distribuce Pareto – Lévy“, které považoval za lepší popis cen akcií a komodit než běžné rozdělení.

Definice

Která není degenerovaný distribuce je distribuční stabilní, jestliže splňuje následující vlastnosti:

Nechť X ₁ a X ₂ být nezávislý kopií náhodné veličiny X . Pak je X považováno za stabilní, pokud pro jakékoli konstanty a > 0 a b > 0 má náhodná proměnná aX ₁ + bX ₂ stejné rozdělení jako cX + d pro některé konstanty c > 0 a d . Distribuce je prý přísně stabilní, pokud to platí s d = 0 .

Protože normální distribuce , Cauchyho distribuce a Lévyho distribuce mají všechny výše uvedené vlastnosti, vyplývá z toho, že se jedná o speciální případy stabilních distribucí.

Taková rozdělení tvoří čtyřparametrovou rodinu spojitých rozdělení pravděpodobnosti parametrizovaných parametry umístění a měřítka μ a c , respektive, a dvěma tvarovými parametry β a α , zhruba odpovídajícími mírám asymetrie a koncentrace (viz obrázky).

Charakteristická funkce φ ( t ) podle kteréhokoliv z rozdělení pravděpodobnosti je jen Fourierova transformace jeho hustoty pravděpodobnosti funkce f ( x ). Funkce hustoty je tedy inverzní Fourierovou transformací charakteristické funkce.

${\ Displaystyle f (x) = {\ frac {1} {2 \ pi}} \ int _ {-\ infty}^{\ infty} \ varphi (t) e^{-ixt} \, dt}$

Ačkoli funkci hustoty pravděpodobnosti pro obecnou stabilní distribuci nelze zapsat analyticky, obecnou charakteristickou funkci lze vyjádřit analyticky. Náhodná proměnná X se nazývá stabilní, pokud její charakteristickou funkci lze zapsat jako

${\ Displaystyle \ varphi (t; \ alpha, \ beta, c, \ mu) = \ exp \ left (it \ mu -| ct |^{\ alpha} \ left (1 -i \ beta \ operatorname {sgn} (t) \ Phi \ right) \ right)}$

kde sgn ( t ) je jen znamení o t a

${\ Displaystyle \ Phi = {\ begin {cases} \ tan \ left ({\ frac {\ pi \ alpha} {2}} \ right) & \ alpha \ neq 1 \\-{\ frac {2} {\ pi}} \ log | ct | & \ alpha = 1 \ end {případy}}}$

μ ∈ R je parametr posunu, β ∈ [−1, 1], nazývaný parametr šikmosti , je mírou asymetrie. Všimněte si, že v tomto kontextu není obvyklá šikmost dobře definována, protože u α <2 distribuce nepřipouští 2. nebo vyšší momenty a obvyklá definice šikmosti je 3. centrální moment .

Důvod, proč to dává stabilní rozdělení, je ten, že charakteristická funkce pro součet dvou nezávislých náhodných proměnných se rovná součinu dvou odpovídajících charakteristických funkcí. Sečtením dvou náhodných proměnných ze stabilní distribuce získáte něco se stejnými hodnotami α a β , ale možná s různými hodnotami μ a c .

Ne každá funkce je charakteristickou funkcí legitimního rozdělení pravděpodobnosti (tj. Funkce , jejíž kumulativní distribuční funkce je skutečná a pohybuje se od 0 do 1 bez snížení), ale výše uvedené charakteristické funkce budou legitimní, pokud jsou v jejich parametrech rozsahy. Hodnota charakteristické funkce při nějaké hodnotě t je komplexní konjugát její hodnoty at - t, jak by měla být, takže funkce rozdělení pravděpodobnosti bude skutečná.

V nejjednodušším případě β = 0 je charakteristická funkce pouze roztaženou exponenciální funkcí ; distribuce je symetrická přibližně μ a je označována jako (Lévy) symetrická alfa-stabilní distribuce , často zkráceně SαS .

Když α <1 a β = 1, rozdělení je podporováno [ μ , ∞).

Parametr c > 0 je faktor měřítka, který je měřítkem šířky distribuce, zatímco α je exponent nebo index distribuce a určuje asymptotické chování distribuce.

Parametrizace

Výše uvedená definice je pouze jednou z parametrizací používaných pro stabilní distribuce; je nejběžnější, ale není spojitý v parametrech při α = 1 .

Souvislá parametrizace je

${\ Displaystyle \ varphi (t; \ alpha, \ beta, \ gamma, \ delta) = \ exp \ left (it \ delta -| \ gamma t |^{\ alpha} \ left (1 -i \ beta \ operatorname {sgn} (t) \ Phi \ right) \ right)}$

kde:

${\ Displaystyle \ Phi = {\ begin {cases} \ left (| \ gamma t |^{1- \ alpha} -1 \ right) \ tan \ left ({\ tfrac {\ pi \ alpha} {2}} \ right) & \ alpha \ neq 1 \\-{\ frac {2} {\ pi}} \ log | \ gamma t | & \ alpha = 1 \ end {cases}}}$

Rozsahy α a β jsou stejné jako dříve, γ (jako c ) by mělo být kladné a δ (jako μ ) by mělo být skutečné.

V každé parametrizaci lze provést lineární transformaci náhodné proměnné a získat náhodnou proměnnou, jejíž hustota je . V první parametrizaci se to provádí definováním nové proměnné: ${\ Displaystyle f (y; \ alpha, \ beta, 1,0)}$

${\ Displaystyle y = {\ begin {cases} {\ frac {x- \ mu} {\ gamma}} & \ alpha \ neq 1 \\ {\ frac {x- \ mu} {\ gamma}}-\ beta {\ frac {2} {\ pi}} \ ln \ gamma & \ alpha = 1 \ end {cases}}}$

Pro druhou parametrizaci jednoduše použijeme

${\ displaystyle y = {\ frac {x- \ delta} {\ gamma}}}$

bez ohledu na to, co je α . Pokud v první parametrizaci existuje průměr (tj. Α > 1 ), pak se rovná μ , zatímco ve druhé parametrizaci, když průměr existuje, je roven${\ Displaystyle \ delta -\ beta \ gamma \ tan \ left ({\ tfrac {\ pi \ alpha} {2}} \ right).}$

Distribuce

Stabilní distribuce je tedy specifikována výše uvedenými čtyřmi parametry. Lze ukázat, že jakákoli nedegenerovaná stabilní distribuce má hladkou (nekonečně diferencovatelnou) funkci hustoty. Pokud označuje hustotu X a Y je součet nezávislých kopií X : ${\ Displaystyle f (x; \ alpha, \ beta, c, \ mu)}$

${\ Displaystyle Y = \ sum _ {i = 1}^{N} k_ {i} (X_ {i}-\ mu) \,}$

pak Y má hustotu s ${\ Displaystyle {\ tfrac {1} {s}} f (y/s; \ alpha, \ beta, c, 0)}$

${\ Displaystyle s = \ left (\ sum _ {i = 1}^{N} | k_ {i} |^{\ alpha} \ right)^{\ frac {1} {\ alpha}}}$

Asymptotické chování je pro α <2 popsáno :

${\ Displaystyle f (x) \ sim {\ frac {1} {| x |^{1+ \ alpha}}} \ left (c^{\ alpha} (1+ \ operatorname {sgn} (x) \ beta ) \ sin \ left ({\ frac {\ pi \ alpha} {2}} \ right) {\ frac {\ Gamma (\ alpha +1)} {\ pi}} \ right)}$

kde Γ je funkce gama (kromě toho, že když α ≥ 1 a β = ± 1, ocas nezmizí doleva nebo doprava, resp. μ , ačkoli výše uvedený výraz je 0). Toto chování „ těžkého ocasu “ způsobuje, že rozptyl stabilních distribucí je nekonečný pro všechny α <2. Tato vlastnost je znázorněna na grafech log – log níže.

Když α = 2, distribuce Gaussova (viz níže), s ocasy asymptotické exp (- x ² /4 ° C ² ) / (2 c √π).

Jednostranně stabilní distribuce a stabilní distribuce počtu

Když α <1 a β = 1, rozdělení je podporováno [ μ , ∞). Tato rodina se nazývá jednostranně stabilní distribuce . Jeho standardní rozdělení (μ = 0) je definováno jako

${\ Displaystyle L _ {\ alpha} (x) = f \ left (x; \ alpha, 1, \ cos \ left ({\ frac {\ alpha \ pi} {2}} \ right)^{1/\ alpha }, 0 \ right)}$, kde .${\ Displaystyle \ alpha <1}$

Nechť je jeho charakteristická funkce . Tak integrální tvar jeho PDF je (poznámka: ) ${\ Displaystyle q = \ exp (-i \ alpha \ pi /2)}$${\ Displaystyle \ varphi (t; \ alpha) = \ exp \ left (-q | t |^{\ alpha} \ right)}$${\ displaystyle {\ text {Im}} (q) <0}$

${\ Displaystyle {\ begin {aligned} L _ {\ alpha} (x) & = {\ frac {1} {\ pi}} \ Re \ left [\ int _ {-\ infty}^{\ infty} e^ {itx} e^{-q | t |^{\ alpha}} \, dt \ right] \\ & = {\ frac {2} {\ pi}} \ int _ {0}^{\ infty} e ^{-{\ text {Re}} (q) \, t^{\ alpha}} \ sin (tx) \ sin (-{\ text {Im}} (q) \, t^{\ alpha}) \, dt, {\ text {nebo}} \\ & = {\ frac {2} {\ pi}} \ int _ {0}^{\ infty} e^{-{\ text {Re}} (q ) \, t^{\ alpha}} \ cos (tx) \ cos ({\ text {Im}} (q) \, t^{\ alpha}) \, dt. \\\ end {aligned}}}$

Integrál s dvojitým sinusem je účinnější pro velmi malé . ${\ displaystyle x}$

Uvažujme Lévyho součet kde , pak Y má hustotu kde . Set , dospějeme ke stabilnímu rozdělení počtu . Jeho standardní distribuce je definována jako ${\ Displaystyle Y = \ sum _ {i = 1}^{N} X_ {i}}$${\ Displaystyle X_ {i} \ sim L _ {\ alpha} (x)}$${\ displaystyle {\ frac {1} {\ nu}} L _ {\ alpha} \ left ({\ frac {x} {\ nu}} \ right)}$${\ Displaystyle \ nu = N^{1/\ alpha}}$${\ displaystyle x = 1}$

${\ displaystyle {\ mathfrak {N}} _ {\ alpha} (\ nu) = {\ frac {\ alpha} {\ Gamma \ left ({\ frac {1} {\ alpha}} \ right)}} { \ frac {1} {\ nu}} L _ {\ alpha} \ left ({\ frac {1} {\ nu}} \ right)}$, kde a .${\ displaystyle \ nu> 0}$${\ Displaystyle \ alpha <1}$

Distribuce stabilního počtu je konjugát před jednostrannou stabilní distribucí. Jeho rodina škály umístění je definována jako

${\ Displaystyle {\ mathfrak {N}} _ {\ alpha} (\ nu; \ nu _ {0}, \ theta) = {\ frac {\ alpha} {\ Gamma ({\ frac {1} {\ alpha }})}} {\ frac {1} {\ nu -\ nu _ {0}}} L _ {\ alpha} \ left ({\ frac {\ theta} {\ nu -\ nu _ {0}}} \že jo)}$, Kde , a .${\ displaystyle \ nu> \ nu _ {0}}$${\ displaystyle \ theta> 0}$${\ Displaystyle \ alpha <1}$

Je to také jednostranná distribuce podporovaná . Parametr umístění je mezní umístění a definuje jeho měřítko. ${\ displaystyle [\ nu _ {0}, \ infty)}$${\ displaystyle \ nu _ {0}}$${\ displaystyle \ theta}$

Pokud , je Lévy distribuce , která je inverzní distribuce gama. Takto je posunuté rozdělení gama tvaru 3/2 a měřítka , ${\ displaystyle \ alpha = {\ frac {1} {2}}}$${\ displaystyle L _ {\ frac {1} {2}} (x)}$${\ displaystyle {\ mathfrak {N}} _ {\ frac {1} {2}} (\ nu; \ nu _ {0}, \ theta)}$${\ Displaystyle 4 \ theta}$

${\ Displaystyle {\ mathfrak {N}} _ {\ frac {1} {2}} (\ nu; \ nu _ {0}, \ theta) = {\ frac {1} {4 {\ sqrt {\ pi }} \ theta^{3/2}}} (\ nu -\ nu _ {0})^{1/2} e^{ -{\ frac {\ nu -\ nu _ {0}} {4 \ theta}}}}$, Kde , .${\ displaystyle \ nu> \ nu _ {0}}$${\ displaystyle \ theta> 0}$

Jeho průměr je a jeho standardní odchylka je . Předpokládá se, že VIX je distribuován jako s a (viz část 7). Tak rozdělení počtu stabilní je prvního řádu marginální rozložení procesu volatility. V této souvislosti se nazývá „nestálost podlahy“. ${\ displaystyle \ nu _ {0} +6 \ theta}$${\ displaystyle {\ sqrt {24}} \ theta}$${\ displaystyle {\ mathfrak {N}} _ {\ frac {1} {2}} (\ nu; \ nu _ {0}, \ theta)}$${\ displaystyle \ nu _ {0} = 10,4}$${\ displaystyle \ theta = 1,6}$${\ displaystyle \ nu _ {0}}$

Dalším přístupem k odvození distribuce stabilního počtu je použít Laplaceovu transformaci jednostranného stabilního rozdělení (část 2.4)

${\ Displaystyle \ int _ {0}^{\ infty} e^{-zx} L _ {\ alpha} (x) dx = e^{-z^{\ alpha}}}$, kde .${\ Displaystyle \ alpha <1}$

Nechť a jeden může rozložit integrál na levé straně jako distribuci produktu standardní Laplaceovy distribuce a standardní stabilní distribuci počtu, ${\ Displaystyle x = 1/\ nu}$

${\ Displaystyle \ int _ {0}^{\ infty} {\ frac {1} {\ nu}} \ left ({\ frac {1} {2}} e^{-{\ frac {| z |} {\ nu}}} \ right) \ left ({\ frac {\ alpha} {\ Gamma ({\ frac {1} {\ alpha}})}} {\ frac {1} {\ nu}} L_ { \ alpha} ({\ frac {1} {\ nu}}) \ right) d \ nu = {\ frac {1} {2}} {\ frac {\ alpha} {\ Gamma ({\ frac {1} {\ alpha}})}} e^{-| z |^{\ alpha}}}$, kde .${\ Displaystyle \ alpha <1}$

Tomu se říká „rozklad lambda“ (viz část 4), protože pravá strana byla v Lihnově dřívějších dílech pojmenována jako „symetrická distribuce lambda“. Má však několik populárnějších názvů, jako je „ exponenciální distribuce výkonu “ nebo „generalizovaná chyba/normální distribuce“, často označovaná jako α > 1.

N -tý okamžik je -tý okamžik , všechny pozitivní momenty jsou konečné. To svým způsobem řeší ožehavou otázku rozbíhajících se momentů ve stabilní distribuci. ${\ displaystyle {\ mathfrak {N}} _ {\ alpha} (\ nu)}$${\ displaystyle -(n+1)}$${\ displaystyle L _ {\ alpha} (x)}$

Vlastnosti

• Všechny stabilní distribuce jsou nekonečně dělitelné .
• S výjimkou normální distribuce ( α = 2) jsou stabilní distribuce leptokurtotické a těžce sledované distribuce .
• Uzavření pod konvolucí

Stabilní distribuce jsou uzavřeny pod konvolucí pro pevnou hodnotu α . Protože konvoluce je ekvivalentní násobení Fourierově transformované funkce, vyplývá z toho, že součin dvou stabilních charakteristických funkcí se stejným α poskytne další takovou charakteristickou funkci. Součin dvou stabilních charakteristických funkcí je dán vztahem:

${\ Displaystyle \ exp \ left (it \ mu _ {1}+it \ mu _ {2}-| c_ {1} t |^{\ alpha}-| c_ {2} t |^{\ alpha}+ i \ beta _ {1} | c_ {1} t |^{\ alpha} \ operatorname {sgn} (t) \ Phi +i \ beta _ {2} | c_ {2} t |^{\ alpha} \ jméno operátora {sgn} (t) \ Phi \ right)}$

Protože Φ není funkcí proměnných μ , c nebo β, vyplývá z toho, že tyto parametry pro konvolvovanou funkci jsou dány vztahem:

${\ Displaystyle {\ begin {aligned} \ mu & = \ mu _ {1}+\ mu _ {2} \\ | c | & = \ left (| c_ {1} |^{\ alpha}+| c_ {2} |^{\ alpha} \ right)^{\ frac {1} {\ alpha}} \\ [6pt] \ beta & = {\ frac {\ beta _ {1} | c_ {1} |^ {\ alpha}+\ beta _ {2} | c_ {2} |^{\ alpha}} {| c_ {1} |^{\ alpha}+| c_ {2} |^{\ alpha}}} \ end {aligned}}}$

V každém případě může být ukázáno, že výsledné parametry leží v požadovaných intervalech pro stabilní rozdělení.

Zobecněná centrální limitní věta

Další důležitou vlastností stabilních distribucí je role, kterou hrají v generalizované centrální limitní větě . Věta o centrálním limitu uvádí, že součet řady nezávislých a identicky distribuovaných (iid) náhodných proměnných s konečnými nenulovými odchylkami bude mít tendenci k normálnímu rozdělení, jak počet proměnných roste.

Zobecnění v důsledku Gnedenka a Kolmogorova uvádí, že součet několika náhodných proměnných se symetrickým rozdělením, které mají mocninové ocasy ( Paretovy ocasy ), klesající jako kde (a tedy s nekonečným rozptylem), bude mít tendenci ke stabilnímu rozdělení jako číslo summandů roste. Pokud pak součet konverguje ke stabilnímu rozdělení s parametrem stability rovným 2, tj. Gaussovo rozdělení. ${\ Displaystyle | x |^{ -\ alpha -1}}$${\ Displaystyle 0 <\ alpha \ leqslant 2}$${\ Displaystyle f (x; \ alpha, 0, c, 0)}$${\ Displaystyle \ alpha> 2}$

Jsou i další možnosti. Pokud je například charakteristická funkce náhodné proměnné asymptotická pro malá t (kladná nebo záporná), můžeme se ptát, jak se t mění s n, když se hodnota charakteristické funkce pro součet n takových náhodných proměnných rovná dané hodnota u : ${\ Displaystyle 1+a | t |^{\ alpha} \ ln | t |}$

${\ Displaystyle \ varphi _ {\ text {sum}} = \ varphi ^{n} = u}$

Za předpokladu, že v tuto chvíli t → 0, vezmeme limit výše jako n → ∞ :

${\ Displaystyle \ ln u = \ lim _ {n \ to \ infty} n \ ln \ varphi = \ lim _ {n \ to \ infty} na | t |^{\ alpha} \ ln | t |.}$

Proto:

${\ Displaystyle {\ begin {aligned} \ ln (\ ln u) & = \ ln \ left (\ lim _ {n \ to \ infty} na | t |^{\ alpha} \ ln | t | \ right) \\ [5pt] & = \ lim _ {n \ to \ infty} \ ln \ left (na | t |^{\ alpha} \ ln | t | \ right) = \ lim _ {n \ to \ infty} \ left \ {\ ln (na)+\ alpha \ ln | t |+\ ln (\ ln | t |) \ right \} \ end {aligned}}}$

To ukazuje, že je to bez použití předchozí rovnice, kterou máme ${\ Displaystyle \ ln | t |}$${\ Displaystyle {\ tfrac {-1} {\ alpha}} \ ln n,}$

${\ Displaystyle | t | \ sim \ left ({\ frac {-\ alpha \ ln u} {na \ ln n}} \ right)^{1/\ alpha}.}$

To znamená, že součet dělen

${\ Displaystyle \ left ({\ frac {na \ ln n} {\ alpha}} \ right)^{\ frac {1} {\ alpha}}}$

má charakteristickou funkci, jejíž hodnota v nějakém t ′ jde do u (jak se n zvyšuje), když Jinými slovy, charakteristická funkce konverguje bodově k, a proto podle Lévyho věty o kontinuitě součet dělený ${\ Displaystyle t '= (-\ ln u)^{\ frac {1} {\ alpha}}.}$${\ Displaystyle \ exp (-(t ')^{\ alpha})}$

${\ Displaystyle \ left ({\ frac {na \ ln n} {\ alpha}} \ right)^{\ frac {1} {\ alpha}}}$

konverguje v distribuci na symetrickou alfa-stabilní distribuci s parametrem stability a parametrem měřítka 1. ${\ Displaystyle \ alpha}$

To lze použít na náhodnou proměnnou, jejíž ocasy se zmenšují jako . Tato náhodná proměnná má průměr, ale rozptyl je nekonečný. Vezměme si následující distribuci: ${\ displaystyle | x |^{-3}}$

${\ Displaystyle f (x) = {\ begin {cases} {\ frac {1} {3}} & | x | \ leqslant 1 \\ {\ frac {1} {3}} x^{-3} & | x |> 1 \ end {případy}}}$

Můžeme to napsat jako

${\ Displaystyle f (x) = \ int _ {1}^{\ infty} {\ frac {2} {w^{4}}} h \ left ({\ frac {x} {w}} \ right) dw}$

kde

${\ Displaystyle h \ left ({\ frac {x} {w}} \ right) = {\ begin {cases} {\ frac {1} {2}} & \ left | {\ frac {x} {w} } \ right | <1, \\ 0 & \ left | {\ frac {x} {w}} \ right |> 1. \ end {cases}}}$

Chceme najít vedoucí termíny asymptotického rozšíření charakteristické funkce. Charakteristická funkce rozdělení pravděpodobnosti je tedy charakteristická funkce pro f ( x ) je ${\ displaystyle {\ tfrac {1} {w}} h \ left ({\ tfrac {x} {w}} \ right)}$${\ displaystyle {\ tfrac {\ sin (tw)} {tw}},}$

${\ Displaystyle \ varphi (t) = \ int _ {1}^{\ infty} {\ frac {2 \ sin (tw)} {tw^{4}}} dw}$

a můžeme vypočítat:

${\ Displaystyle {\ begin {aligned} \ varphi (t) -1 & = \ int _ {1}^{\ infty} {\ frac {2} {w^{3}}} \ left [{\ frac {\ sin (tw)} {tw}}-1 \ right] \, dw \\ & = \ int _ {1}^{\ frac {1} {| t |}} {\ frac {2} {w^{ 3}}} \ left [{\ frac {\ sin (tw)} {tw}}-1 \ right] \, dw+\ int _ {\ frac {1} {| t |}}^{\ infty} { \ frac {2} {w^{3}}} \ left [{\ frac {\ sin (tw)} {tw}}-1 \ right] \, dw \\ & = \ int _ {1}^{ \ frac {1} {| t |}} {\ frac {2} {w^{3}}} \ left [{\ frac {\ sin (tw)} {tw}}-1+ \ left \ {- {\ frac {t^{2} w^{2}} {3!}}+{\ frac {t^{2} w^{2}} {3!}} \ right \} \ right] \, dw+\ int _ {\ frac {1} {| t |}}^{\ infty} {\ frac {2} {w^{3}}} \ left [{\ frac {\ sin (tw)} {tw }}-1 \ right] \, dw \\ & = \ int _ {1}^{\ frac {1} {| t |}}-{\ frac {t^{2} dw} {3w}}+ \ int _ {1}^{\ frac {1} {| t |}} {\ frac {2} {w^{3}}} \ left [{\ frac {\ sin (tw)} {tw}} -1+{\ frac {t^{2} w^{2}} {3!}} \ Right] dw+\ int _ {\ frac {1} {| t |}}^{\ infty} {\ frac {2} {w^{3}}} \ left [{\ frac {\ sin (tw)} {tw}}-1 \ right] dw \\ & = \ int _ {1}^{\ frac {1 } {| t |}}-{\ frac {t^{2} dw} {3w}}+\ left \ {\ int _ {0}^{\ frac {1} {| t |}} {\ frac {2} {w^{3}}} \ left [{\ frac {\ sin (tw)} {tw}}-1+{\ frac {t^{2} w^{2}} {3!} } \ right] dw- \ int _ {0}^{1} {\ frac {2} {w^{3 }}} \ left [{\ frac {\ sin (tw)} {tw}}-1+{\ frac {t^{2} w^{2}} {3!}} \ right] dw \ right \ }+\ int _ {\ frac {1} {| t |}}^{\ infty} {\ frac {2} {w^{3}}} \ left [{\ frac {\ sin (tw)} { tw}}-1 \ vpravo] dw \\ & = \ int _ {1}^{\ frac {1} {| t |}}-{\ frac {t^{2} dw} {3w}}+t ^{2} \ int _ {0}^{1} {\ frac {2} {y^{3}}} \ left [{\ frac {\ sin (y)} {y}}-1+{\ frac {y^{2}} {6}} \ right] dy- \ int _ {0}^{1} {\ frac {2} {w^{3}}} \ left [{\ frac {\ sin (tw)} {tw}}-1+{\ frac {t^{2} w^{2}} {6}} \ right] dw+t^{2} \ int _ {1}^{\ infty } {\ frac {2} {y^{3}}} \ left [{\ frac {\ sin (y)} {y}}-1 \ right] dy \\ & =-{\ frac {t^{ 2}} {3}} \ int _ {1}^{\ frac {1} {| t |}} {\ frac {dw} {w}}+t^{2} C_ {1}-\ int _ {0}^{1} {\ frac {2} {w^{3}}} \ left [{\ frac {\ sin (tw)} {tw}}-1+{\ frac {t^{2} w^{2}} {6}} \ right] dw+t^{2} C_ {2} \\ & = {\ frac {t^{2}} {3}} \ ln | t |+t^ {2} C_ {3}-\ int _ {0}^{1} {\ frac {2} {w^{3}}} \ left [{\ frac {\ sin (tw)} {tw}}- 1+{\ frac {t^{2} w^{2}} {6}} \ right] dw \\ & = {\ frac {t^{2}} {3}} \ ln | t |+t ^{2} C_ {3}-\ int _ {0}^{1} {\ frac {2} {w^{3}}} \ left [{\ frac {t^{4} w^{4} } {5!}}+\ Cdots \ right] dw \\ & = {\ frac {t^{2}} {3}} \ ln | t |+t^{2} C_ {3}-{\ mathcal {O}} \ left (t^{4} \ right) \ end {al ignorováno}}}$

kde a jsou konstanty. Proto, ${\ displaystyle C_ {1}, C_ {2}}$${\ displaystyle C_ {3}}$

${\ Displaystyle \ varphi (t) \ sim 1+{\ frac {t^{2}} {3}} \ ln | t |}$

a podle toho, co bylo řečeno výše (a skutečnosti, že rozptyl f ( x ; 2,0,1,0) je 2), součet n instancí této náhodné veličiny, děleno vůlí, se v distribuci sbíhá do Gaussova rozdělení s rozptylem 1. Rozptyl v kterémkoli konkrétním n však bude stále nekonečný. Všimněte si toho, že šířka omezujícího rozdělení roste rychleji než v případě, kde má náhodná proměnná konečný rozptyl (v takovém případě šířka roste jako odmocnina n ). Průměru , získá dělením součtu o n , inklinuje k Gaussian, jehož šířka se blíží k nule, jak n se zvyšuje, v souladu se zákonem velkých čísel . ${\ Displaystyle {\ sqrt {n (\ ln n)/12}},}$

Speciální případy

Záznam log-log symetrické centrované stabilní distribuce PDF ukazující chování mocninného zákona pro velká x . Chování mocninného zákona dokládá přímočarý vzhled PDF pro velká x , se sklonem rovným-( α + 1). (Jedinou výjimkou je α = 2 v černé barvě, což je normální rozdělení.)

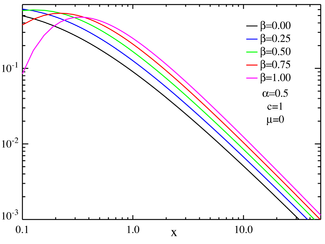
Protokol log-log zkosené středové stabilní distribuce PDF zobrazující chování mocninného zákona pro velká x . Sklon lineárních částí je opět roven - ( α + 1)

Obecné analytické řešení pro formu f ( x ) neexistuje . Existují však tři zvláštní případy, které lze vyjádřit pomocí elementárních funkcí, jak je vidět na inspekci charakteristické funkce :

• Pro α = 2 se rozdělení sníží na Gaussovo rozdělení s rozptylem σ ² = 2 c ² a průměrem μ ; parametr šikmosti β nemá žádný účinek.
• Pro α = 1 a β = 0 se rozdělení sníží na Cauchyovo rozdělení s parametrem měřítka c a parametrem posunu μ .
• Pro α = 1/2 a β = 1 se rozdělení sníží na Lévyho rozdělení s parametrem měřítka c a parametrem posunu μ .

Všimněte si, že výše uvedené tři distribuce jsou také spojeny následujícím způsobem: Na standardní Cauchyho náhodnou proměnnou lze pohlížet jako na směs Gaussových náhodných proměnných (všechny s průměrnou nulou), přičemž rozptyl je čerpán ze standardní Lévyho distribuce. A ve skutečnosti se jedná o speciální případ obecnější věty (viz str. distribuce míchání - a parametr beta distribuce míchání se vždy rovná jedné).

Pro G-funkce Meijer je k dispozici obecný výraz uzavřeného formuláře pro stabilní PDF s racionálními hodnotami α . Fox H-Functions lze také použít k vyjádření stabilních funkcí hustoty pravděpodobnosti. U jednoduchých racionálních čísel je výraz uzavřeného tvaru často ve smyslu méně komplikovaných speciálních funkcí . K dispozici je několik výrazů uzavřené formy s poměrně jednoduchými výrazy, pokud jde o speciální funkce. V níže uvedené tabulce jsou PDF vyjádřitelné elementárními funkcemi označeny E a ty, které jsou vyjádřitelné speciálními funkcemi, jsou označeny s .

Některé speciální případy jsou známy pod určitými názvy:

• Pro α = 1 a β = 1 je distribuce Landauova distribuce, která má pod tímto názvem specifické využití ve fyzice.
• Pro α = 3/2 a β = 0 se distribuce redukuje na Holtsmarkovu distribuci s parametrem měřítka c a parametrem posunu μ .

Rovněž v limitu, jak se c blíží nule, nebo jak se α blíží nule, se rozdělení přiblíží k Diracově delta funkci δ ( x  -  μ ) .

Zastoupení řady

Stabilní distribuci lze přepsat jako skutečnou součást jednoduššího integrálu:

${\ Displaystyle f (x; \ alpha, \ beta, c, \ mu) = {\ frac {1} {\ pi}} \ Re \ left [\ int _ {0}^{\ infty} e^{it (x- \ mu)} e^{-(ct)^{\ alpha} (1-i \ beta \ Phi)} \, dt \ right].}$

Vyjádříme -li druhý exponenciál jako Taylorovu řadu , máme:

${\ Displaystyle f (x; \ alpha, \ beta, c, \ mu) = {\ frac {1} {\ pi}} \ Re \ left [\ int _ {0}^{\ infty} e^{it (x- \ mu)} \ sum _ {n = 0}^{\ infty} {\ frac {(-qt^{\ alpha})^{n}} {n!}} \, dt \ right]}$

kde . Obrácení pořadí integrace a součtu a provedení integračních výnosů: ${\ Displaystyle q = c^{\ alpha} (1-i \ beta \ Phi)}$

${\ Displaystyle f (x; \ alpha, \ beta, c, \ mu) = {\ frac {1} {\ pi}} \ Re \ left [\ sum _ {n = 1}^{\ infty} {\ frac {(-q)^{n}} {n!}} \ left ({\ frac {i} {x- \ mu}} \ right)^{\ alpha n+1} \ Gamma (\ alpha n+ 1) \ vpravo]}$

které budou platné pro x ≠ μ a budou konvergovat pro příslušné hodnoty parametrů. (Všimněte si, že termín n = 0, který poskytuje funkci delta v x - μ, byl proto vynechán.) Vyjádření první exponenciály jako řady poskytne další řadu v kladných mocnostech x - μ, což je obecně méně užitečné.

Pro jednostranně stabilní distribuci je třeba výše uvedené rozšíření řady upravit, protože a . Neexistuje žádná skutečná část k součtu. Místo toho by integrál charakteristické funkce měl být prováděn na záporné ose, což dává: ${\ Displaystyle q = \ exp (-i \ alpha \ pi /2)}$${\ Displaystyle qi^{\ alpha} = 1}$

${\ Displaystyle {\ begin {aligned} L _ {\ alpha} (x) & = {\ frac {1} {\ pi}} \ Re \ left [\ sum _ {n = 1}^{\ infty} {\ frac {(-q)^{n}} {n!}} \ left ({\ frac {-i} {x}} \ right)^{\ alpha n+1} \ Gamma (\ alpha n+1) \ right] \\ & = {\ frac {1} {\ pi}} \ sum _ {n = 1}^{\ infty} {\ frac {-\ sin (n (\ alpha +1) \ pi)} {n!}} \ left ({\ frac {1} {x}} \ right)^{\ alpha n+1} \ Gamma (\ alpha n+1) \\\ end {aligned}}}$

Simulace stabilních proměnných

Simulace sekvencí stabilních náhodných proměnných není přímočará, protože pro inverzní ani pro samotný CDF neexistují žádné analytické výrazy . Všechny standardní přístupy, jako jsou metody odmítnutí nebo inverze, by vyžadovaly únavné výpočty. Mnohem elegantnější a efektivnější řešení navrhli Chambers, Mallows a Stuck (CMS), kteří si všimli, že určitý integrální vzorec poskytl následující algoritmus: ${\ displaystyle F^{-1} (x)}$${\ displaystyle F (x)}$

• generovat náhodně proměnnou rovnoměrně rozloženou na a nezávislou exponenciální náhodnou proměnnou s průměrem 1;${\ displaystyle U}$${\ displaystyle \ left (-{\ tfrac {\ pi} {2}}, {\ tfrac {\ pi} {2}} \ right)}$${\ displaystyle W}$
• pro výpočet:${\ Displaystyle \ alpha \ neq 1}$

${\ Displaystyle X = \ left (1+ \ zeta ^{2} \ right) ^{\ frac {1} {2 \ alpha}} {\ frac {\ sin (\ alpha (U+\ xi))} {( \ cos (U))^{\ frac {1} {\ alpha}}}} \ \ left ({\ frac {\ cos (U- \ alpha (U+\ xi))} {W}} \ right)^{ \ frac {1- \ alpha} {\ alpha}},}$

• pro výpočet:${\ Displaystyle \ alpha = 1}$

${\ Displaystyle X = {\ frac {1} {\ xi}} \ left \ {\ left ({\ frac {\ pi} {2}}+\ beta U \ right) \ tan U- \ beta \ log \ vlevo ({\ frac {{\ frac {\ pi} {2}} W \ cos U} {{\ frac {\ pi} {2}}+\ beta U}} \ right) \ right \},}$

kde

${\ Displaystyle \ zeta =-\ beta \ tan {\ frac {\ pi \ alpha} {2}}, \ qquad \ xi = {\ begin {cases} {\ frac {1} {\ alpha}} \ arctan ( -\ zeta) & \ alpha \ neq 1 \\ {\ frac {\ pi} {2}} & \ alpha = 1 \ end {cases}}}$

Tento algoritmus poskytuje náhodnou proměnnou . Podrobný důkaz viz. ${\ Displaystyle X \ sim S _ {\ alpha} (\ beta, 1,0)}$

Vzhledem k tomu vzorců pro simulaci standardního stabilní náhodné veličiny, můžeme snadno simulovat stabilní náhodnou proměnnou pro všechny přípustné hodnoty parametrů , , a pomocí následující vlastnosti. Pokud ano ${\ Displaystyle \ alpha}$${\ displaystyle c}$${\ displaystyle \ beta}$${\ Displaystyle \ mu}$${\ Displaystyle X \ sim S _ {\ alpha} (\ beta, 1,0)}$

${\ Displaystyle Y = {\ begin {cases} cX+\ mu & \ alpha \ neq 1 \\ cX+{\ frac {2} {\ pi}} \ beta c \ log c+\ mu & \ alpha = 1 \ end { případy}}}$

je . Pro (a ) způsob CMS snižuje k dobře známému Box-Muller transformace pro generování Gaussova náhodné veličiny. V literatuře bylo navrženo mnoho dalších přístupů, včetně aplikace rozšíření řady Bergström a LePage, viz resp. Metoda CMS je však považována za nejrychlejší a nejpřesnější. ${\ Displaystyle S _ {\ alpha} (\ beta, c, \ mu)}$${\ Displaystyle \ alpha = 2}$${\ displaystyle \ beta = 0}$

Aplikace

Stabilní distribuce vděčí za svůj význam v teorii i praxi zobecnění centrální limitní věty na náhodné veličiny bez momentů druhého (a možná prvního) řádu a doprovodné vlastní podobnosti stabilní rodiny. Právě zdánlivý odklon od normality spolu s poptávkou po podobném modelu finančních dat (tj. Tvar rozdělení ročních změn cen aktiv by měl připomínat základní denní nebo měsíční změny cen) vedl Benoîta Mandelbrota k návrhu že ceny bavlny sledují alfa-stabilní distribuci s α rovnou 1,7. Distribuce Lévy se často nachází v analýze kritického chování a finančních údajů.

Nacházejí se také ve spektroskopii jako obecný výraz pro kvazistaticky tlakově rozšířenou spektrální čáru .

Lévyho distribuce čekacích časů slunečních erupcí (doba mezi událostmi vzplanutí) byla prokázána u pevných rentgenových slunečních erupcí CGRO BATSE v prosinci 2001. Analýza Lévyho statistického podpisu odhalila, že byly patrné dva různé podpisy paměti; jeden souvisí se slunečním cyklem a druhý, jehož původ se zdá být spojen s lokalizovaným nebo kombinací lokalizovaných efektů sluneční aktivní oblasti.

Jiné analytické případy

Je známa řada případů analyticky exprimovatelných stabilních distribucí. Nechť je stabilní rozdělení vyjádřeno do té doby, víme: ${\ Displaystyle f (x; \ alpha, \ beta, c, \ mu)}$

• Cauchy distribuce je dána${\ Displaystyle f (x; 1,0,1,0).}$
• Distribuce Lévy je dána${\ Displaystyle f (x; {\ tfrac {1} {2}}, 1,1,0).}$
• Normální rozdělení je dána${\ Displaystyle f (x; 2,0,1,0).}$
• Nechť je Lommelova funkce , pak:${\ Displaystyle S _ {\ mu, \ nu} (z)}$

${\ Displaystyle f \ left (x; {\ tfrac {1} {3}}, 0,1,0 \ right) = \ Re \ left ({\ frac {2e^{-{\ frac {i \ pi} {4}}} {3 {\ sqrt {3}} \ pi}} {\ frac {1} {\ sqrt {x^{3}}}} S_ {0, {\ frac {1} {3} }} \ left ({\ frac {2e^{\ frac {i \ pi} {4}}} {3 {\ sqrt {3}}}} {\ frac {1} {\ sqrt {x}}} \ dobře dobře)}$

• Označme a označme Fresnelovy integrály :${\ Displaystyle S (x)}$${\ Displaystyle C (x)}$

${\ Displaystyle f \ left (x; {\ tfrac {1} {2}}, 0,1,0 \ right) = {\ frac {1} {\ sqrt {2 \ pi | x |^{3}} }} \ left (\ sin \ left ({\ tfrac {1} {4 | x |}} \ right) \ left [{\ frac {1} {2}}-S \ left ({\ tfrac {1} {\ sqrt {2 \ pi | x |}}} \ right) \ right]+\ cos \ left ({\ tfrac {1} {4 | x |}} \ right) \ left [{\ frac {1} {2}}-C \ left ({\ tfrac {1} {\ sqrt {2 \ pi | x |}}} \ right) \ right] \ right)}$

• Nechť je upravená Besselova funkce druhého druhu pak:${\ displaystyle K_ {v} (x)}$

${\ Displaystyle f \ left (x; {\ tfrac {1} {3}}, 1,1,0 \ right) = {\ frac {1} {\ pi}} {\ frac {2 {\ sqrt {2 }}} {3^{\ frac {7} {4}}}} {\ frac {1} {\ sqrt {x^{3}}}} K _ {\ frac {1} {3}} \ left ( {\ frac {4 {\ sqrt {2}}} {3^{\ frac {9} {4}}}} {\ frac {1} {\ sqrt {x}}} \ right)}$

• Pokud označují hypergeometrické funkce, pak:${\ displaystyle {} _ {m} F_ {n}}$

${\ Displaystyle {\ begin {aligned} f \ left (x; {\ tfrac {4} {3}}, 0,1,0 \ right) & = {\ frac {3^{\ frac {5} {4 }}} {4 {\ sqrt {2 \ pi}}}} {\ frac {\ Gamma \ left ({\ tfrac {7} {12}} \ right) \ Gamma \ left ({\ tfrac {11} { 12}} \ right)} {\ Gamma \ left ({\ tfrac {6} {12}} \ right) \ Gamma \ left ({\ tfrac {8} {12}} \ right)}} {} _ { 2} F_ {2} \ left ({\ tfrac {7} {12}}, {\ tfrac {11} {12}}; {\ tfrac {6} {12}}, {\ tfrac {8} {12 }}; {\ tfrac {3^{3} x^{4}} {4^{4}}} \ right)-{\ frac {3^{\ frac {11} {4}} x^{3 }} {4^{3} {\ sqrt {2 \ pi}}}} {\ frac {\ Gamma \ left ({\ tfrac {13} {12}} \ right) \ Gamma \ left ({\ tfrac { 17} {12}} \ right)} {\ Gamma \ left ({\ tfrac {18} {12}} \ right) \ Gamma \ left ({\ tfrac {15} {12}} \ right)}} { } _ {2} F_ {2} \ left ({\ tfrac {13} {12}}, {\ tfrac {17} {12}}; {\ tfrac {18} {12}}, {\ tfrac {15 } {12}}; {\ tfrac {3^{3} x^{4}} {4^{4}}} \ right) \\ [6pt] f \ left (x; {\ tfrac {3} { 2}}, 0,1,0 \ right) & = {\ frac {\ Gamma \ left ({\ tfrac {5} {3}} \ right)} {\ pi}} {} _ {2} F_ { 3} \ left ({\ tfrac {5} {12}}, {\ tfrac {11} {12}}; {\ tfrac {1} {3}}, {\ tfrac {1} {2}}, { \ tfrac {5} {6}};-{\ tfrac {2^{2} x^{6}} {3^{6}}} \ right)-{\ frac {x^{2}} {3 \ pi}} {} _ {3} F_ {4} \ l eft ({\ tfrac {3} {4}}, 1, {\ tfrac {5} {4}}; {\ tfrac {2} {3}}, {\ tfrac {5} {6}}, {\ tfrac {7} {6}}, {\ tfrac {4} {3}};-{\ tfrac {2^{2} x^{6}} {3^{6}}} \ right)+{\ frac {7x^{4} \ Gamma \ left ({\ tfrac {4} {3}} \ right)} {3^{4} \ pi^{2}}} {} _ {2} F_ {3} \ left ({\ tfrac {13} {12}}, {\ tfrac {19} {12}}; {\ tfrac {7} {6}}, {\ tfrac {3} {2}}, {\ tfrac {5} {3}};-{\ tfrac {2^{2} x^{6}} {3^{6}}} \ right) \ end {aligned}}}$

přičemž druhou jmenovanou je distribuce Holtsmark .

• Nechť je funkce Whittaker , pak:${\ Displaystyle W_ {k, \ mu} (z)}$

${\ Displaystyle {\ begin {aligned} f \ left (x; {\ tfrac {2} {3}}, 0,1,0 \ right) & = {\ frac {\ sqrt {3}} {6 {\ sqrt {\ pi}} | x |}} \ exp \ left ({\ tfrac {2} {27}} x^{-2} \ right) W _ {-{\ frac {1} {2}}, { \ frac {1} {6}}} \ left ({\ tfrac {4} {27}} x^{-2} \ right) \\ [8pt] f \ left (x; {\ tfrac {2} { 3}}, 1,1,0 \ vpravo) & = {\ frac {\ sqrt {3}} {{\ sqrt {\ pi}} | x |}} \ exp \ left (-{\ tfrac {16} {27}} x^{-2} \ right) W _ {{\ frac {1} {2}}, {\ frac {1} {6}}} \ left ({\ tfrac {32} {27}} x^{-2} \ right) \\ [8pt] f \ left (x; {\ tfrac {3} {2}}, 1,1,0 \ right) & = {\ begin {cases} {\ frac {\ sqrt {3}} {{\ sqrt {\ pi}} | x |}} \ exp \ left ({\ frac {1} {27}} x^{3} \ right) W _ {{\ frac { 1} {2}}, {\ frac {1} {6}}} \ left (-{\ frac {2} {27}} x^{3} \ right) & x <0 \\ {} \\ { \ frac {\ sqrt {3}} {6 {\ sqrt {\ pi}} | x |}} \ exp \ left ({\ frac {1} {27}} x^{3} \ right) W _ {- {\ frac {1} {2}}, {\ frac {1} {6}}} \ left ({\ frac {2} {27}} x^{3} \ right) & x \ geq 0 \ end { případy}} \ end {aligned}}}$

Viz také

• Lévyho let
• Lévyho proces
• Další distribuce „mocenského práva“
  • Paretova distribuce
  • Distribuce Zeta
  • Distribuce Zipf
  • Distribuce Zipf – Mandelbrot
• Stabilní a temperované stabilní distribuce s klastrováním volatility - finanční aplikace
• Vícerozměrná stabilní distribuce
• Diskrétně stabilní distribuce

Poznámky

• Program STABLE pro Windows je k dispozici na stabilní webové stránce Johna Nolana: http://www.robustanalysis.com/public/stable.html . Vypočítává hustotu (pdf), kumulativní distribuční funkci (cdf) a kvantily pro obecnou stabilní distribuci a provádí odhad maximální pravděpodobnosti stabilních parametrů a některé techniky průzkumné analýzy dat pro posouzení vhodnosti sady dat.
• libstable je implementace C pro stabilní distribuční funkce pdf, cdf, náhodné číslo, kvantil a přizpůsobovací funkce (spolu s balíčkem replikace benchmarku a balíčkem R).
• R Package 'stabledist' od Diethelma Wuertze, Martina Maechlera a členů Rmetrics. Vypočítá stabilní hustotu, pravděpodobnost, kvantily a náhodná čísla. Aktualizováno 12. září 2016.

Reference