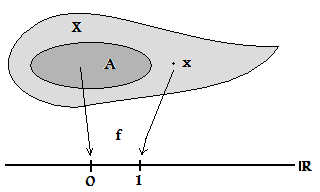
Tychonoffův prostor - Tychonoff space
|
Separační axiomy v topologických prostorech | |
|---|---|
| Kolmogorovova klasifikace | |
| T 0 | (Kolmogorov) |
| T 1 | (Fréchet) |
| T 2 | (Hausdorff) |
| T 2 ½ | (Urysohn) |
| úplně T 2 | (zcela Hausdorff) |
| T 3 | (běžný Hausdorff) |
| T 3½ | (Tychonoff) |
| T 4 | (normální Hausdorff) |
| T 5 | (úplně normální Hausdorff) |
| T 6 | (naprosto normální Hausdorff) |
V topologii a příbuzných oborech matematiky jsou Tychonoffovy prostory a zcela pravidelné prostory druhy topologických prostorů . Tyto podmínky jsou příklady separačních axiomů .
Tychonoffovy prostory jsou pojmenovány po Andrey Nikolajeviči Tychonoffovi , jehož ruský název (Тихонов) je různě interpretován jako „Tychonov“, „Tikhonov“, „Tihonov“, „Tichonov“ atd., Který je zavedl v roce 1930, aby se vyhnul patologické situaci Hausdorffa prostory, jejichž jedinou souvislou skutečnou funkcí jsou konstantní mapy.
Definice
Topologický prostor se nazývá zcela pravidelný, pokud lze body oddělit od uzavřených množin pomocí (ohraničených) spojitých funkcí se skutečnou hodnotou. Z technického hlediska to znamená: pro každou uzavřenou sadu a jakýkoli bod existuje na reálná spojitá funkce taková, že a (Ekvivalentně je možné zvolit jakékoli dvě hodnoty místo a , a dokonce vyžadují, aby je omezená funkce).
Topologický prostor se nazývá Tychonoffův prostor (alternativně: T 3½ prostor , nebo T π prostor , nebo úplně T 3 prostor ), pokud se jedná o zcela normální Hausdorffův prostor .
Poznámka. Zcela pravidelné prostory a Tychonoffovy prostory jsou spojeny prostřednictvím pojmu Kolmogorovovy ekvivalence . Topologický prostor je Tychonoff právě tehdy, je-li zcela normální a T 0 . Na druhou stranu je prostor zcela pravidelný právě tehdy, je-li jeho Kolmogorovovým kvocientem Tychonoff.
Konvence pojmenování
V celé matematické literatuře se používají různé konvence, pokud jde o termíny „zcela normální“ a „T“. Definice v této části jsou v typickém moderním použití. Někteří autoři však mění význam těchto dvou druhů výrazů nebo všechny výrazy používají zaměnitelně. Na Wikipedii se výrazy „zcela normální“ a „Tychonoff“ používají volně a „T“ poznámkám se obecně vyhýbáme. Ve standardní literatuře se proto doporučuje opatrnost při zjišťování, jaké definice autor používá. Další informace o tomto problému najdete v části Historie separačních axiomů .
Příklady a protiklady
Téměř každý topologický prostor studovaný v matematické analýze je Tychonoff, nebo alespoň úplně pravidelný. Například skutečná čára je Tychonoff pod standardní euklidovskou topologií . Mezi další příklady patří:
- Každý metrický prostor je Tychonoff; každý pseudometrický prostor je zcela pravidelný.
- Každý místně kompaktní pravidelný prostor je zcela pravidelný, a proto každý místně kompaktní prostor Hausdorff je Tychonoff.
- Zejména každé topologické potrubí je Tychonoff.
- Každá úplně objednaná sada s topologií objednávky je Tychonoff.
- Každá topologická skupina je zcela pravidelná.
- Zobecněním metrických prostorů a topologických skupin je každý jednotný prostor zcela pravidelný. Platí to i naopak: každý zcela běžný prostor je uniformovatelný.
- Každý komplex CW je Tychonoff.
- Každý normální regulární prostor je zcela pravidelný a každý normální Hausdorffův prostor je Tychonoff.
- Niemytzki rovina je příkladem Tychonoff prostoru, který není normální .
Vlastnosti
Zachování
Úplná pravidelnost a vlastnost Tychonoff se chovají dobře s ohledem na počáteční topologie . Konkrétně je zachována úplná pravidelnost převzetím libovolných počátečních topologií a vlastnost Tychonoff je zachována převzetím počátečních topologií oddělujících body. Z toho vyplývá, že:
- Každý podprostor zcela běžného nebo Tychonoffova prostoru má stejnou vlastnost.
- Neprázdný produktový prostor je zcela běžný (respektive Tychonoff) právě tehdy, když je každý faktorový prostor zcela běžný (respektive Tychonoff).
Stejně jako všechny separační axiomy není úplná pravidelnost zachována přijetím konečné topologie . Zejména kvocienty zcela pravidelných mezer nemusí být pravidelné . Kvocienty Tychonoffových prostorů nemusí být ani Hausdorff . Existují uzavřené kvocienty Mooreovy roviny, které poskytují protiklady.
Skutečné spojité funkce
Pro jakýkoli topologický prostor X nechme C ( X ) označit rodinu spojitých funkcí se skutečnou hodnotou na X a nechme C b ( X ) podmnožinou omezených spojitých funkcí se skutečnou hodnotou.
Zcela pravidelné prostory lze charakterizovat tím, že jejich topologie je zcela určena pomocí C ( X ) nebo C b ( X ). Zejména:
- Prostor X je zcela pravidelný právě tehdy, pokud má počáteční topologii vyvolanou C ( X ) nebo C b ( X ).
- Prostor X je zcela pravidelný právě tehdy, když lze každou uzavřenou množinu zapsat jako průnik rodiny nulových množin v X (tj. Nulové množiny tvoří základ uzavřených množin X ).
- Prostor X je zcela pravidelný tehdy a jen tehdy, pokud cozero sady z X, tvoří základ pro topologii X. .
Vzhledem k libovolnému topologickému prostoru ( X , τ) existuje univerzální způsob přidružení zcela regulárního prostoru k ( X , τ). Nechť ρ je počáteční topologie na X indukovaná C τ ( X ) nebo ekvivalentně topologie generovaná na základě součtových součinů v ( X , τ). Pak ρ bude nejlepší úplně pravidelná topologie na X, která je hrubší než τ. Tato konstrukce je univerzální v tom smyslu, že každá spojitá funkce
do zcela normálního prostoru Y bude spojitý na ( X , ρ). V jazyce teorie kategorií je funktor, který vysílá ( X , τ) na ( X , ρ), adjungován s funktorem začlenění CReg → Nahoru . Tak skupina zcela pravidelné mezery CREG je reflexní podkategorii z vrcholu , na kategorii topologických prostorů . Když vezmeme Kolmogorovovy kvocienty , zjistíme , že podkategorie Tychonoffových prostorů je také reflexní.
Lze prokázat, že C τ ( X ) = C ρ ( X ) ve výše uvedené konstrukci, takže prstence C ( X ) a C b ( X ) jsou obvykle studovány pouze pro zcela pravidelné prostory X .
Kategorie realcompact Tychonoffových prostorů je anti-ekvivalentní kategorii prstenců C ( X ) (kde X je realcompact) společně s prstencovými homomorfismy jako mapy. Například je možné rekonstruovat X z C ( X ), když X je (skutečné) kompaktní. Algebraická teorie těchto kruhů je proto předmětem intenzivních studií. Rozsáhlé zobecnění této třídy prstenů, které stále připomíná mnoho vlastností Tychonoffových prostorů, ale je použitelné i ve skutečné algebraické geometrii , je třída skutečných uzavřených prstenů .
Vkládání
Tychonoffovy prostory jsou přesně ty prostory, které lze vložit do kompaktních Hausdorffových prostorů . Přesněji řečeno, pro každou Tychonoff prostor X , existuje kompaktní Hausdorff prostoru K takové, že X je homeomorphic do podprostoru K .
Ve skutečnosti lze vždy zvolit K jako kostku Tychonoff (tj. Možná nekonečný součin jednotkových intervalů ). Každá Tychonoffova kostka je kompaktní Hausdorff jako důsledek Tychonoffovy věty . Protože každý podprostor kompaktního Hausdorffova prostoru je Tychonoff, má jeden:
- Topologický prostor je Tychonoff právě tehdy, když může být vložen do krychle Tychonoff .
Zhutnění
Zvláště zajímavé jsou ty, kde embeddings obraz X je hustá v K ; tito jsou nazýváni Hausdorffovy compactifications z X . Vzhledem k tomu, žádné vkládání a Tychonoff prostoru X, v kompaktním Hausdorff prostoru K uzávěr z obrazu X v K je kompaktní obal z X . Ve stejném článku z roku 1930, kde Tychonoff definoval zcela pravidelné prostory, také dokázal, že každý Tychonoffův prostor má Hausdorffovo zhutnění.
Mezi těmito Hausdorffových compactifications, je jedinečný „nejobecnější“ jeden je kamene Čech kompaktifikace β X . To se vyznačuje tím, univerzální vlastnost , že, vzhledem k tomu, kontinuální mapa f z X na jinou kompaktní Hausdorff prostoru Y , existuje unikátní kontinuální mapa g z beta X na Y , která se rozkládá f v tom smyslu, že f je složení z g a j .
Jednotné struktury
Úplná pravidelnost je přesně podmínkou nezbytnou pro existenci jednotných struktur v topologickém prostoru. Jinými slovy, každý jednotný prostor má zcela pravidelnou topologii a každý zcela běžný prostor X je uniformizovatelný . Topologický prostor připouští samostatnou jednotnou strukturu právě tehdy, je-li to Tychonoff.
Vzhledem k tomu, zcela pravidelný prostor X je obvykle více než jeden uniformity na X , který je kompatibilní s topologií X . Vždy však bude existovat nejlepší kompatibilní uniformita, která se na X nazývá jemná uniformita . Pokud X je Tychonoff, pak je jednotná struktura může být zvolena tak, že β X stane dokončení jednotného prostoru X .
Citace
Bibliografie
- Gillman, Leonard ; Jerison, Meyer (1960). Kruhy spojitých funkcí . Graduate Texts in Mathematics, No. 43 (Dover reprint ed.). NY: Springer-Verlag. p. xiii. ISBN 978-048681688-3.
- Narici, Lawrence ; Beckenstein, Edward (2011). Topologické vektorové prostory . Čistá a aplikovaná matematika (druhé vydání). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834 .
- Willard, Stephen (1970). Obecná topologie (vydání Dover, vyd.). Reading, Massachusetts: Addison-Wesley Publishing Company. ISBN 0-486-43479-6.