Úhlová trisekce - Angle trisection

Úhly mohou být trisected přes neusis konstrukci pomocí nástrojů mimo neoznačené pravítko a kompas. Příklad ukazuje trisekci libovolného úhlu

θ>.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} 3π/4

pravítkem s délkou rovnající se poloměru kružnice, přičemž půlicí úhel

φ = θ / 3

.

Trisekce úhlu je klasickým problémem stavby pravítka a kompasu starověké řecké matematiky . Jedná se o konstrukci úhlu rovnajícího se jedné třetině daného libovolného úhlu za použití pouze dvou nástrojů: neoznačeného pravítka a kompasu .

Pierre Wantzel v roce 1837 dokázal, že problém, jak je uvedeno, není možné vyřešit pro libovolné úhly. Ačkoli obecně neexistuje způsob, jak trisektovat úhel pouhým kompasem a pravítkem, některé speciální úhly lze rozdělit. Například je poměrně jednoduché trisektovat pravý úhel (tj. Sestrojit úhel o velikosti 30 stupňů).

Je možné trisect libovolný úhel pomocí nástrojů jiných než pravítko a kompas. Například konstrukce Neusis , známá také starověkým Řekům, zahrnuje současné klouzání a otáčení značeného pravítka , čehož nelze dosáhnout původními nástroji. Matematici během staletí vyvinuli další techniky.

Protože je definován jednoduše, ale je složitý, aby se ukázal jako neřešitelný, je problém úhlové trisekce častým předmětem pseudomatematických pokusů o řešení naivních nadšenců. Tato „řešení“ často zahrnují mylné interpretace pravidel nebo jsou prostě nesprávná.

Pozadí a prohlášení o problému

Půlení z libovolných úhlů již dávno vyřešena.

Pomocí pouze neoznačeného pravítka a kompasu našli řečtí matematici prostředky k rozdělení čáry na libovolnou sadu stejných segmentů, k kreslení rovnoběžných čar, k půlení úhlů , ke konstrukci mnoha polygonů a ke konstrukci čtverců o stejné nebo dvojnásobné ploše daný mnohoúhelník.

Tři problémy se ukázaly jako nepolapitelné, konkrétně trisekcí úhlu, zdvojnásobením krychle a čtvercováním kruhu . Problém úhlové trisekce zní:

Vytvořte úhel rovný jedné třetině daného libovolného úhlu (nebo jej rozdělte na tři stejné úhly) pomocí pouze dvou nástrojů:

neoznačená pravítka, a
kompas.

Důkaz nemožnosti

Pravítka . Zobrazené jsou označeny-ideální pravítko je bez označení

Kružítko

Pierre Wantzel publikoval důkaz nemožnosti klasického rozřezání libovolného úhlu v roce 1837. Wantzelův důkaz, přepracovaný v moderní terminologii, používá koncept rozšíření pole , téma, které je nyní typicky kombinováno s Galoisovou teorií . Wantzel však publikoval tyto výsledky dříve než Évariste Galois (jehož práce, napsaná v roce 1830, byla publikována až v roce 1846) a nepoužíval koncepty zavedené Galoisem.

Problém sestrojení úhlu dané míry $θ$ je ekvivalentní konstrukci dvou segmentů tak, že poměr jejich délky je $cos θ$ . Od řešení k jednomu z těchto dvou problémů může jeden přejít k řešení druhého pomocí konstrukce kompasu a pravítka. Triple-úhel vzorec dává výraz vztahující se cosines původního úhlu a jeho roztrojení: $cos θ$ = $4 cos 3 θ / 3 - 3 cos θ / 3$ .

Z toho vyplývá, že vzhledem k segmentu, který je definován tak, aby měl jednotkovou délku, je problém úhlové trisekce ekvivalentní konstrukci segmentu, jehož délka je kořenem krychlového polynomu . Tato ekvivalence redukuje původní geometrický problém na čistě algebraický problém.

Každé racionální číslo je konstruovatelné. Každé iracionální číslo, které je konstruovatelné v jednom kroku z nějakých daných čísel, je kořenem polynomu stupně 2 s koeficienty v poli generovanými těmito čísly. Proto každé číslo, které je konstruovatelné sekvencí kroků, je kořenem minimálního polynomu, jehož stupeň je mocnina dvou . Úhel $π / 3$ radiány (60 stupňů , psáno 60 °) je konstruovatelné . Níže uvedený argument ukazuje, že není možné sestrojit úhel 20 °. To znamená, že úhel 60 ° nelze rozdělit na třetiny, a tedy ani libovolný úhel nelze rozdělit.

Značí množinu racionálních čísel ze strany $Q$ . Pokud by bylo možné rozdělit na 60 °, stupeň minimálního polynomu $cos 20 °$ nad $Q$ by byl mocninou dvou. Nyní nechť $x = cos 20 °$ . Všimněte si, že $cos 60 °$ = $cos π / 3$ = $1 / 2$ . Potom podle vzorce s trojitým úhlem $cos π / 3 = 4 x 3 - 3 x$ a tak $4 x 3 - 3 x = 1 / 2$ . Tedy $8 x 3 - 6 x - 1 = 0$ . Definujte $p (t)$ jako polynom $p (t) = 8 t 3 - 6 t - 1$ .

Protože $x = cos 20 °$ je kořenem $p (t)$ , minimální polynom pro $cos 20 °$ je faktor $p (t)$ . Protože $p (t)$ má stupeň 3, pokud je redukovatelný na $Q,$ pak má racionální kořen . Podle racionální kořenové věty musí být tento kořen $\pm 1, \pm 1 / 2, \pm 1 / 4$ nebo $\pm 1 / 8$ , ale žádný z nich není root. Z tohoto důvodu, $p (t)$ je nesnížitelný přes které $Q$ , a minimální polynom pro $cos 20 °$ je ze stupně $3$ .

Měřicí úhel $60 °$ tedy nelze rozdělit.

Úhly, které lze rozdělit

Některé úhly však mohou být zkráceny. Například pro jakýkoli konstruovatelný úhel $θ$ může být úhel $3 θ$ triviálně trisektován ignorováním daného úhlu a přímým vytvořením úhlu $θ$ . Existují úhly, které nejsou konstruovatelné, ale jsou trisektibilní (přestože samotný třetinový úhel není konstruovatelný). Například, $3 π / 7$ je takový úhel: pět úhlů měření $3 π / 7$ spojte a vytvořte úhel měření $15 π / 7$ , což je celý kruh plus požadovaný $π / 7$ .

Pro kladné celé číslo $N$ je úhel měření $2 π / N.$ je trisectible tehdy a jen tehdy, pokud $3$ nerozděluje $N$ . V porovnání, $2 π / N.$ je konstruovatelný právě tehdy, když $N$ je mocnina $2$ nebo součin síly $2$ s součinem jedné nebo více odlišných Fermatových prvočísel .

Algebraická charakteristika

Opět platí, že značí množinu racionálních čísel od $Q$ .

Věta : Měřicí úhel $θ$ může být trisektován pouze tehdy, pokud $q (t) = 4 t 3 - 3 t - cos (θ)$ je redukovatelné přes rozšíření pole $Q (cos (θ))$ .

Důkaz je poměrně jednoduché zobecnění důkazu dané výše, že $60 °$ úhel není trisectible.

Jiné metody

Obecný problém úhlové trisekce je řešitelný pomocí dalších nástrojů, a jde tedy mimo původní řecký rámec kompasu a pravítka.

Bylo navrženo mnoho nesprávných metod trisekcí obecného úhlu. Některé z těchto metod poskytují rozumnou aproximaci; jiné (některé z nich jsou uvedeny níže) zahrnují nástroje, které nejsou v klasickém problému povoleny. Matematik Underwood Dudley popsal některé z těchto neúspěšných pokusů ve své knize Trisektory .

Aproximace postupnými půleními

Trisekci lze aproximovat opakováním metody kompasu a pravítka pro půlení úhlu. Geometrická řada1/3 = 1/4 + 1/16 + 1/64 + 1/256+ ⋯ nebo1/3 = 1/2 - 1/4 + 1/8 - 1/16+ ⋯ lze použít jako základ pro půlení. Aproximaci libovolného stupně přesnosti lze získat v konečném počtu kroků.

Pomocí origami

Trisekci, jako mnoho konstrukcí nemožných pravítkem a kompasem, lze snadno dosáhnout skládáním papíru nebo origami . Huzitiny axiomy (typy skládacích operací) mohou konstruovat kubické rozšíření (odmocniny) daných délek, zatímco pravítko a kompas může konstruovat pouze kvadratické rozšíření (odmocniny).

Pomocí propojení

Sylvester's Link Fan

Existuje řada jednoduchých vazeb, které lze použít k vytvoření nástroje pro rozřezávání úhlů, včetně Kempeho Trisector a Sylvester's Link Fan nebo Isoklinostat.

S pravoúhlým trojúhelníkovým pravítkem

Bieberbachova trisekce úhlu (modře) pomocí pravoúhlého pravítka (červeně)

V roce 1932 publikoval Ludwig Bieberbach v časopise Journal für die reine und angewandte Mathematik své dílo Zur Lehre von den kubischen Konstruktionen . Uvádí v něm (volný překlad):

„ Jak je známo ... každou kubickou konstrukci lze vysledovat zpět na trisekci úhlu a na násobení krychle, tj. Extrakci třetího kořene. Stačí mi ukázat, jak tyto dva klasické úkoly mohou být vyřešeno pomocí pravoúhlého háku. “

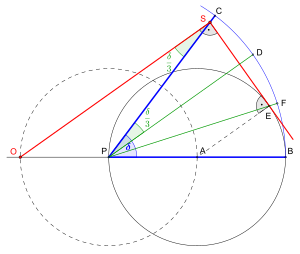
Konstrukce začíná nakreslením kružnice procházející vrcholem $P$ úhlu, který má být trisektován, se středem na $A$ na hraně tohoto úhlu a $B$ jako druhým průsečíkem s hranou. Kružnici se středem na $P$ a se stejným poloměrem, protíná linie podporující výhodu v $A$ a $O$ .

Nyní je na výkres umístěno pravé trojúhelníkové pravítko následujícím způsobem: jedna noha jeho pravého úhlu prochází $O$ ; jehož vrchol jeho pravého úhlu je umístěna v bodě $S$ v řádku $PC$ takovým způsobem, že druhé rameno pravítka je tečna v $E$ do kružnice se středem $A$ . Z toho vyplývá, že původní úhel je trisected čarou $PE$ , a linka $PD$ kolmo k $SE$ a procházející $P$ . Tuto čáru lze nakreslit buď opět použitím pravoúhlého pravoúhlého pravítka, nebo použitím tradiční konstrukce pravítka a kompasu . S podobnou konstrukcí, je možné zvýšit polohu $E$ , s použitím, že je průsečíkem čáry $SE$ a jeho kolmou procházejícího $A$ .

Důkaz: Jeden má dokázat rovnosti úhlů a tři řádky $OS$ , $PD$ a $AE$ jsou rovnoběžné. Protože úsečky $OP$ a $PA$ jsou si rovny, tyto tři rovnoběžné čáry ohraničují dva stejné segmenty na každé další sečné čáře, a zejména na jejich společné kolmé $JV$ . Tedy $SD$ $'$ $=$ $D$ $'$ $E$ , kde $D '$ je průsečík přímek $PD$ a $SE$ . Z toho vyplývá, že pravé trojúhelníky $PD$ $'$ $S$ a $PD$ $'$ $E$ jsou shodné, a tedy že první požadovaná rovnost. Na druhou stranu, trojúhelník $PAE$ je rovnoramenný , protože všechny poloměry kruhu jsou si rovny; to znamená, že jeden má také, protože tyto dva úhly jsou alternativní úhly příčných ke dvěma rovnoběžným čarám. To dokazuje druhou požadovanou rovnost, a tedy správnost konstrukce. ${\ displaystyle {\ widehat {EPD}} = {\ widehat {DPS}}}$ ${\ displaystyle {\ widehat {BPE}} = {\ widehat {EPD}}.}$ ${\ displaystyle {\ widehat {EPD}} = {\ widehat {DPS}},}$ ${\ displaystyle {\ widehat {APE}} = {\ widehat {AEP}}.}$ ${\ displaystyle {\ widehat {AEP}} = {\ widehat {EPD}},}$

S pomocnou křivkou

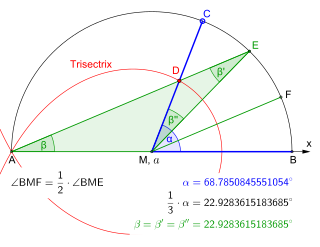
Trisekce pomocí archimédovské spirály
Trisekce pomocí Maclaurin trisectrix

Existují určité křivky nazývané trisectrices, které, pokud jsou nakresleny v rovině jinými metodami, mohou být použity k trisect libovolných úhlů. Příklady zahrnují trisectrix Colin Maclaurin , uvedený v kartézských souřadnicích , které implicitní rovnici

{\ Displaystyle 2x (x^{2}+y^{2}) = a (3x^{2} -y^{2}),}

a Archimédova spirála . Spirálu lze ve skutečnosti použít k rozdělení úhlu na libovolný počet stejných částí.

S vyznačeným pravítkem

Trisekce úhlu pomocí označeného pravítka

Dalším způsobem, jak rozdělit libovolný úhel „malým“ krokem mimo řecký rámec, je pravítko se dvěma značkami, které jsou od sebe vzdáleny. Dalším stavba je původně kvůli Archimedes , který se nazývá Neusis konstrukce , tj která využívá nástroje jiné než un-označený pravítkem. Použité diagramy ukazují tuto konstrukci pro ostrý úhel, ale ve skutečnosti funguje pro jakýkoli úhel až do 180 stupňů.

To vyžaduje tři fakta z geometrie (vpravo):

Jakákoli úplná sada úhlů na přímce se zvyšuje o 180 °,
Součet úhlů nějakého trojúhelníku je 180 °, a ,
Jakékoli dvě stejné strany rovnoramenného trojúhelníku se setkají s třetí ve stejném úhlu .

Nechť $l$ je vodorovná čára v sousedním diagramu. Úhel $a$ (vlevo od bodu $B$ ) je předmětem trisekce. Za prvé, bod je nakreslena v úhlu v paprsku , jedna jednotka na rozdíl od $B$ . Nakreslí se kruh o poloměru $AB$ . Potom se výraznost panovníka přichází do hry: jedna značka pravítka je umístěna na $A$ a druhý v $B$ . Zatímco se pravítko (ale ne značka) dotýká $A$ , pravítko se posouvá a otáčí, dokud jedna značka není na kruhu a druhá na přímce $l$ . Značka na kruhu je označen $C$ a značka na trati je označen $D$ . Tím je zajištěno, že $CD$ $=$ $AB$ . Nakreslí se poloměr $BC,$ aby bylo zřejmé, že všechny úsečky $AB$ , $BC$ a $CD$ mají stejnou délku. Nyní, trojúhelníky $ABC$ a $BCD$ jsou rovnoramenný , tedy (o Fact 3 výše), každý z nich má dva stejné úhly.

Hypotéza : Vzhledem k tomu, že $AD$ je přímka a $AB$ , $BC$ a $CD$ mají všechny stejnou délku,

Závěr : úhel $b = A / 3$ .

Důkaz :

Z faktu 1) výše, °. ${\ displaystyle e+c = 180}$
Při pohledu na trojúhelník BCD , ze skutečnosti 2) °. ${\ displaystyle e+2b = 180}$
Z posledních dvou rovnic . ${\ displaystyle c = 2b}$
Od faktu 2), °, tedy ° , tedy od posledního, ° . ${\ Displaystyle d+2c = 180}$ ${\ displaystyle d = 180}$ ${\ displaystyle -2c}$ ${\ displaystyle d = 180}$ ${\ displaystyle -4b}$
Od faktu 1) výše, °, tedy ° °. ${\ displaystyle a+d+b = 180}$ ${\ displaystyle a+(180}$ ${\ displaystyle -4b)+b = 180}$

Vymazání, $a - 3 b = 0$ , nebo $a = 3 b$ , a věta je prokázána .

Opět platí, že tato konstrukce vyšel na rámec z povolených staveb pomocí výrazné pravítka.

S provázkem

Thomas Hutcheson publikoval v Učiteli matematiky článek, který místo kompasu a rovné hrany používal strunu. Řetězec lze použít buď jako rovnou hranu (natažením), nebo jako kompas (upevněním jednoho bodu a identifikací jiného), ale může také obepnout válec, klíč k Hutchesonovu řešení.

Hutcheson sestrojil válec z úhlu, který má být roztržen, nakreslením oblouku přes úhel, jeho dokončením jako kruh a z tohoto kruhu sestrojením válce, na kterém byl napsán, řekněme, rovnostranný trojúhelník (úhel 360 stupňů rozdělen na tři ). Toto bylo poté „namapováno“ na úhel, který má být roztržen, s jednoduchým důkazem podobných trojúhelníků.

S „tomahawkem“

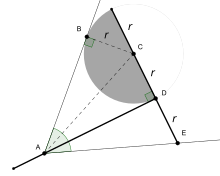
Tomahawk rozřezávající úhel. Tomahawk je tvořen tlustými čarami a stínovaným půlkruhem.

„ Tomahawk “ je geometrický tvar skládající se z půlkruhu a dvou ortogonálních úseček, takže délka kratšího segmentu se rovná poloměru kruhu. Trisekce se provede tak, že se konec kratšího segmentu tomahawku nakloní na jeden paprsek, okraj kruhu na druhý, takže „rukojeť“ (delší segment) překročí vrchol úhlu; trisekční čára probíhá mezi vrcholem a středem půlkruhu.

Tomahawk je konstruovatelný pomocí kompasu a pravítka, ale obecně není možné postavit tomahawk v jakékoli požadované poloze. Výše uvedená konstrukce tedy není v rozporu s nespojitelností úhlů pouze pomocí pravítka a kompasu.

Protože tomahawk může být použit jako množina čtverců , může být také použit pro tříúhelníkové úhly metodou popsanou v § S pravoúhlým pravoúhlým pravítkem .

Tomahawk vytváří stejný geometrický efekt jako metoda skládání papíru: vzdálenost mezi středem kruhu a špičkou kratšího segmentu je dvojnásobkem vzdálenosti poloměru, který je zaručeně v kontaktu s úhlem. Je také ekvivalentní použití architektů L-Ruler ( Tesařské náměstí ).

S propojenými kompasy

Úhel lze rozdělit pomocí zařízení, které je v podstatě čtyřpólovou verzí kompasu, s vazbami mezi hroty navrženými tak, aby byly tři úhly mezi sousedními hroty stejné.

Využití úhlové trisekce

Animace neusisovy konstrukce sedmiúhelníku s poloměrem kružnice podle Andrewa M. Gleasona , využívající trisekci úhlu pomocí tomahawku

{\ displaystyle {\ overline {OA}} = 6}

Kubické rovnice s reálnými koeficienty mohou být řešeny geometricky s kompasem, pravítkem a úhel trisector tehdy a jen tehdy, když má tři reálné kořeny .

Pravidelný mnohoúhelník s n stranami mohou být konstruovány s pravítkem, kompasu, a úhel trisector tehdy a pouze tehdy, když , kde r, s, k ≥ 0 a kde p _i jsou různá prvočísla více než 3 z formy (tj Pierpont prvočísla větší než 3 ). ${\ Displaystyle n = 2^{r} 3^{s} p_ {1} p_ {2} \ cdots p_ {k},}$ ${\ Displaystyle 2^{t} 3^{u} +1}$

Zobecnění

Pro jakékoli nenulové celé číslo $N$ lze úhel o velikosti $.mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} 2 π ⁄ N$ radiánů rozdělit na $n$ stejných částí pomocí pravítka a kompasu pouze tehdy, pokud $n$ je buď mocnina $2,$ nebo je síla $2$ vynásobena součinem jednoho nebo více zřetelný Fermat připraví, z nichž žádný rozděluje $N$ . V případě třísekce ( $n = 3$ , což je Fermatova prime), se tato podmínka stává výše uvedeným požadavkem, aby $N$ nebylo dělitelné $3$ .

Viz také

Reference

Další čtení

Courant, Richard, Herbert Robbins, Ian Stewart, Co je to matematika?: Elementární přístup k myšlenkám a metodám , Oxford University Press USA, 1996. ISBN 978-0-19-510519-3 .

externí odkazy

Jiné způsoby trisekce

Přibližná úhlová trisekce jako animace, max. chyba úhlu ≈ ± 4E-8 °
Trisekce přes ( Archivováno 2009-10-25) na limacon z Pascal ; viz také Trisectrix
Trisekce přes za Archimédova spirála
Trisekce prostřednictvím se konchoida z Nicomedes
sciencenews.org o používání origami
Hyperbolická trisekce a spektrum pravidelných polygonů

Languages

In other projects