Bézierova křivka -Bézier curve

Kubická Bézierova křivka se čtyřmi kontrolními body

Bázové funkce na rozsahu t v [0,1] pro kubické Bézierovy křivky: modrá: y = (1 − t ) ³ , zelená: y = 3(1 − t ) ² t , červená: y = 3(1 − t ) t2 a azurová ^: y = t3 . ^_

Bézierova křivka ( / ˈ b ɛ z . i . eɪ / BEH -zee-ay ) je parametrická křivka používaná v počítačové grafice a příbuzných oborech. Sada diskrétních „kontrolních bodů“ definuje hladkou, spojitou křivku pomocí vzorce. Obvykle je křivka určena k aproximaci skutečného tvaru, který jinak nemá žádné matematické vyjádření nebo jehož reprezentace je neznámá nebo příliš komplikovaná. Bézierova křivka je pojmenována po francouzském inženýrovi Pierru Bézierovi , který ji v 60. letech použil pro navrhování křivek pro karoserii Renaultu .auta. Mezi další využití patří návrh počítačových písem a animace. Bézierovy křivky lze zkombinovat za účelem vytvoření Bézierovy spline nebo zobecnit na vyšší rozměry a vytvořit tak Bézierovy plochy . Bézierův trojúhelník je zvláštním případem toho druhého.

Ve vektorové grafice se Bézierovy křivky používají k modelování hladkých křivek, které lze neomezeně měnit. "Cesty", jak jsou běžně označovány v programech pro manipulaci s obrázky, jsou kombinacemi spojených Bézierovych křivek. Cesty nejsou vázány limity rastrovaných obrázků a lze je intuitivně upravovat.

Bézierovy křivky se také používají v časové oblasti, zejména v animaci , designu uživatelského rozhraní a vyhlazování trajektorie kurzoru v rozhraních ovládaných pohledem očí. Například Bézierovu křivku lze použít ke specifikaci rychlosti objektu v čase, jako je pohyb ikony z bodu A do bodu B, namísto pouhého pohybu s pevným počtem pixelů na krok. Když animátoři nebo návrháři rozhraní mluví o „fyzice“ nebo „pocitu“ operace, mohou mít na mysli konkrétní Bézierovu křivku, která se používá k řízení rychlosti daného pohybu v průběhu času.

To platí i pro robotiku, kde by měl být pohyb např. svařovacího ramene plynulý, aby nedocházelo ke zbytečnému opotřebení.

Vynález

Matematický základ pro Bézierovy křivky – Bernsteinovy ​​polynomy – byl založen v roce 1912, ale polynomy byly použity v grafice až o 50 let později, kdy matematik Paul de Casteljau v roce 1959 vyvinul de Casteljauův algoritmus , numericky stabilní metodu pro vyhodnocování křivek, a stal se prvním, kdo je aplikoval na počítačově podporovaný design ve francouzské automobilce Citroën . Přesto byla de Casteljauova metoda patentována ve Francii, ale publikována nebyla až do 80. let, zatímco Bézierovy polynomy byly široce propagovány v 60. letech francouzským inženýrem Pierrem Bézierem , který je objevil nezávisle a použil je k navrhování karoserií automobilů u Renaultu .

Konkrétní případy

Bézierova křivka je definována sadou řídicích bodů P 0 _až P n _, kde n se nazývá řád křivky ( n = 1 pro lineární, 2 pro kvadratický, 3 pro kubický atd.). První a poslední kontrolní body jsou vždy koncovými body křivky; mezilehlé kontrolní body (pokud existují) však obecně neleží na křivce. Součty v následujících částech je třeba chápat jako afinní kombinace – to znamená, že součet koeficientů je 1.

Lineární Bézierovy křivky

Dané odlišné body P ₀ a P ₁ , lineární Bézierova křivka je prostě čára mezi těmito dvěma body. Křivka je dána pomocí

${\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}+t(\mathbf {P} _{1}-\mathbf {P} _{0})=(1-t) \mathbf {P} _{0}+t\mathbf {P} _{1},\ 0\leq t\leq 1}$

a je ekvivalentní lineární interpolaci .

Kvadratické Bézierovy křivky

Kvadratické Bézierovy křivky ve smyčcovém umění : Koncové body ( • ) a kontrolní bod ( × ) definují kvadratickou Bézierovu křivku ( ⋯ ).

Kvadratická Bézierova křivka je dráha, kterou sleduje funkce B ( t ), dané body P ₀ , P ₁ a P ₂ ,

${\displaystyle \mathbf {B} (t)=(1-t)[(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1}]+t[(1- t)\mathbf {P} _{1}+t\mathbf {P} _{2}],\ 0\leq t\leq 1}$,

který lze interpretovat jako lineární interpolant odpovídajících bodů na lineárních Bézierově křivkách od P ₀ do P ₁ a od P ₁ do P ₂ v tomto pořadí. Přeuspořádání předchozí rovnice dává:

${\displaystyle \mathbf {B} (t)=(1-t)^{2}\mathbf {P} _{0}+2(1-t)t\mathbf {P} _{1}+t^ {2}\mathbf {P} _{2},\ 0\leq t\leq 1.}$

To lze zapsat způsobem, který zvýrazní symetrii vzhledem k P ₁ :

${\displaystyle \mathbf {B} (t)=\mathbf {P} _{1}+(1-t)^{2}(\mathbf {P} _{0}-\mathbf {P} _{1 })+t^{2}(\mathbf {P} _{2}-\mathbf {P} _{1}),\ 0\leq t\leq 1.}$

Což okamžitě dává derivaci Bézierovy křivky vzhledem k t :

${\displaystyle \mathbf {B} '(t)=2(1-t)(\mathbf {P} _{1}-\mathbf {P} _{0})+2t(\mathbf {P} _{ 2}-\mathbf {P} _{1}),}$

z čehož lze usoudit, že tečny ke křivce v P ₀ a P ₂ se protínají v P ₁ . Jak se t zvyšuje z _{0 na 1} , křivka se odchýlí od P ₀ ve směru P1 , poté se ohýbá, aby dosáhla _P2 ze směru P1 .

Druhá derivace Bézierovy křivky vzhledem k t je

${\displaystyle \mathbf {B} ''(t)=2(\mathbf {P} _{2}-2\mathbf {P} _{1}+\mathbf {P} _{0}).}$

Kubické Bézierovy křivky

Čtyři body P ₀ , P ₁ , P ₂ a P ₃ v rovině nebo ve vícerozměrném prostoru definují kubickou Bézierovu křivku. Křivka začíná v P ₀ směrem k P ₁ a přichází do P ₃ přicházející ze směru P ₂ . Obvykle neprojde přes P1 nebo _{P2 ;} tyto body slouží pouze k poskytování směrových informací. Vzdálenost mezi P ₁ a P ₂ určuje "jak daleko" a "jak rychle" se křivka pohybuje směrem k P ₁ před otočením směrem k P ₂ .

Zápisem B _{P i , P j , P k} ( t ) pro kvadratickou Bézierovu křivku definovanou body P _i , P _j a P _k lze kubickou Bézierovu křivku definovat jako afinní kombinaci dvou kvadratických Bézierových křivek:

${\displaystyle \mathbf {B} (t)=(1-t)\mathbf {B} _{\mathbf {P} _{0},\mathbf {P} _{1},\mathbf {P} _ {2}}(t)+t\mathbf {B} _{\mathbf {P} _{1},\mathbf {P} _{2},\mathbf {P} _{3}}(t), \ 0\leq t\leq 1.}$

Explicitní tvar křivky je:

${\displaystyle \mathbf {B} (t)=(1-t)^{3}\mathbf {P} _{0}+3(1-t)^{2}t\mathbf {P} _{1 }+3(1-t)t^{2}\mathbf {P} _{2}+t^{3}\mathbf {P} _{3},\ 0\leq t\leq 1.}$

Pro některé volby P ₁ a P ₂ se může křivka protínat nebo obsahovat vrchol .

Libovolnou sérii 4 různých bodů lze převést na kubickou Bézierovu křivku, která prochází všemi 4 body v pořadí. Vzhledem k počátečnímu a koncovému bodu nějaké kubické Bézierovy křivky a bodům podél křivky odpovídajícím t  = 1/3 at  = 2/3 lze získat řídicí body pro původní Bézierovu křivku.

Derivace kubické Bézierovy křivky vzhledem k t is

${\displaystyle \mathbf {B} '(t)=3(1-t)^{2}(\mathbf {P} _{1}-\mathbf {P} _{0})+6(1-t )t(\mathbf {P} _{2}-\mathbf {P} _{1})+3t^{2}(\mathbf {P} _{3}-\mathbf {P} _{2}) \,.}$

Druhá derivace Bézierovy křivky vzhledem k t je

${\displaystyle \mathbf {B} ''(t)=6(1-t)(\mathbf {P} _{2}-2\mathbf {P} _{1}+\mathbf {P} _{0 })+6t(\mathbf {P} _{3}-2\mathbf {P} _{2}+\mathbf {P} _{1})\,.}$

Obecná definice

Bézierovy křivky lze definovat pro libovolný stupeň n .

Rekurzivní definice

Rekurzivní definice Bézierovy křivky stupně n ji vyjadřuje jako point-to-point lineární kombinaci ( lineární interpolace ) dvojice odpovídajících si bodů ve dvou Bézierových křivkách stupně n  − 1.

Označme Bézierovu křivku určenou libovolným výběrem bodů P ₀ , P ₁ , ...,  P _k . Pak začít, ${\displaystyle \mathbf {B} _{\mathbf {P} _{0}\mathbf {P} _{1}\ldots \mathbf {P} _{k}}}$

${\displaystyle \mathbf {B} _{\mathbf {P} _{0}}(t)=\mathbf {P} _{0}{\text{, and}}}$

${\displaystyle \mathbf {B} (t)=\mathbf {B} _{\mathbf {P} _{0}\mathbf {P} _{1}\ldots \mathbf {P} _{n}}( t)=(1-t)\mathbf {B} _{\mathbf {P} _{0}\mathbf {P} _{1}\ldots \mathbf {P} _{n-1}}(t) +t\mathbf {B} _{\mathbf {P} _{1}\mathbf {P} _{2}\ldots \mathbf {P} _{n}}(t)}$

Tato rekurze je vysvětlena v animacích níže .

Explicitní definice

Vzorec lze explicitně vyjádřit následovně (kde t ⁰ a (1-t) ⁰ jsou nepřetržitě rozšířeny na 1 v celém [0,1]):

${\displaystyle {\begin{aligned}\mathbf {B} (t)&=\sum _{i=0}^{n}{n \choose i}(1-t)^{ni}t^{i }\mathbf {P} _{i}\\&=(1-t)^{n}\mathbf {P} _{0}+{n \choose 1}(1-t)^{n-1} t\mathbf {P} _{1}+\cdots +{n \vyberte n-1}(1-t)t^{n-1}\mathbf {P} _{n-1}+t^{n }\mathbf {P} _{n},&&0\leqslant t\leqslant 1\end{aligned}}}$

kde jsou binomické koeficienty . ${\displaystyle \scriptstyle {n \choose i}}$

Například, když n  = 5:

${\displaystyle {\begin{aligned}\mathbf {B} (t)&=(1-t)^{5}\mathbf {P} _{0}+5t(1-t)^{4}\mathbf {P} _{1}+10t^{2}(1-t)^{3}\mathbf {P} _{2}+10t^{3}(1-t)^{2}\mathbf {P } _{3}+5t^{4}(1-t)\mathbf {P} _{4}+t^{5}\mathbf {P} _{5},&&0\leqslant t\leqslant 1.\ konec{aligned}}}$

Terminologie

S těmito parametrickými křivkami je spojena určitá terminologie. My máme

${\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}b_{i,n}(t)\mathbf {P} _{i},\ \ \ 0\leq t \leq 1}$

kde jsou polynomy

${\displaystyle b_{i,n}(t)={n \vyberte i}t^{i}(1-t)^{ni},\ \ \ i=0,\ldots ,n}$

jsou známé jako polynomy Bernsteinovy ​​báze stupně n .

Všimněte si, že t ⁰  = 1, (1 −  t ) ⁰  = 1 a že binomický koeficient , , je: ${\displaystyle \scriptstyle {n \choose i}}$

${\displaystyle {n \choose i}={\frac {n!}{i!(ni)!}}.}$

Body P _i se nazývají řídicí body Bézierovy křivky. Mnohoúhelník vytvořený spojením Bézierových bodů úsečkami , počínaje P ₀ a končícími P n _, se nazývá Bézierův mnohoúhelník (neboli kontrolní polygon ). Konvexní trup Bézierova polygonu obsahuje Bézierovu křivku .

Polynomiální forma

Někdy je žádoucí vyjádřit Bézierovu křivku jako polynom namísto součtu méně přímočarých Bernsteinových polynomů . Aplikace binomického teorému na definici křivky s následným přeskupením přinese výsledek

${\displaystyle \mathbf {B} (t)=\sum _{j=0}^{n}{t^{j}\mathbf {C} _{j}}}$

kde

${\displaystyle \mathbf {C} _{j}={\frac {n!}{(nj)!}}\sum _{i=0}^{j}{\frac {(-1)^{i +j}\mathbf {P} _{i}}{i!(ji)!}}=\prod _{m=0}^{j-1}(nm)\součet _{i=0}^{ j}{\frac {(-1)^{i+j}\mathbf {P} _{i}}{i!(ji)!}}.}$

To by mohlo být praktické, pokud by se to dalo vypočítat před mnoha hodnoceními ; měli byste však být opatrní, protože křivky vysokého řádu mohou postrádat numerickou stabilitu ( pokud k tomu dojde, je třeba použít de Casteljauův algoritmus ). Všimněte si, že prázdný produkt je 1. ${\displaystyle \mathbf {C} _{j}}$${\displaystyle \mathbf {B} (t)}$

Vlastnosti

Kubická Bézierova křivka (žlutá) může být shodná s kvadratickou (černá)

1. kopírování koncových bodů a

2. umístění jejích 2 středních kontrolních bodů (žluté kroužky) 2/3 podél úseček od koncových bodů ke střednímu kontrolnímu bodu kvadratické křivky (černý obdélník).

• Křivka začíná v P ₀ a končí v P _n ; jedná se o takzvanou vlastnost interpolace koncového bodu .
• Křivka je čára právě tehdy, když jsou všechny řídicí body kolineární .
• Začátek a konec křivky je tečný k první a poslední části Bézierova polygonu.
• Křivku lze v libovolném bodě rozdělit na dvě podkřivky nebo na libovolně mnoho podkřivek, z nichž každá je také Bézierovou křivkou.
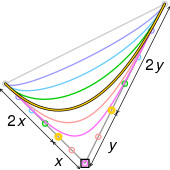
• Některé křivky, které se zdají jednoduché, jako je kruh , nelze přesně popsat Bézierovou nebo po částech Bézierovou křivkou; ačkoli čtyřdílná kubická Bézierova křivka může aproximovat kružnici (viz složená Bézierova křivka ), s maximální radiální chybou menší než jedna část z tisíce, když každý vnitřní kontrolní bod (nebo offline bod) je vzdálenost vodorovně nebo svisle od vnější kontrolní bod na jednotkové kružnici. Obecněji platí, že n - dílná kubická Bézierova křivka může aproximovat kružnici, když každý vnitřní řídicí bod je vzdálenost od vnějšího řídicího bodu na jednotkové kružnici, kde t je 360/ n stupňů a n > 2.${\displaystyle \textstyle {\frac {4\left({\sqrt {2}}-1\right)}{3}}}$${\displaystyle \textstyle {\frac {4}{3}}\tan(t/4)}$
• Každá kvadratická Bézierova křivka je také kubická Bézierova křivka a obecněji, každý stupeň n Bézierova křivka je také křivkou stupně m pro libovolné m > n . V detailu je křivka stupně n s řídicími body P ₀ , ..., P _n ekvivalentní (včetně parametrizace) křivce stupně n + 1 s řídicími body P' ₀ , ..., P' _{n + 1} , kde .${\displaystyle \mathbf {P} '_{k}={\tfrac {k}{n+1}}\mathbf {P} _{k-1}+\left(1-{\tfrac {k}{ n+1}}\vpravo)\mathbf {P} _{k}}$
• Bézierovy křivky mají vlastnost zmenšování variace . Z intuitivního hlediska to znamená, že Bézierova křivka se „nevlní“ více než polygon jejích řídicích bodů a ve skutečnosti se může „vlnit“ méně.
• Neexistuje žádná místní kontrola v Bézierových křivkách stupně n – to znamená, že jakákoli změna kontrolního bodu vyžaduje přepočet, a tak ovlivňuje vzhled celé křivky, „ačkoli čím dále je od kontrolního bodu, který byl změněn, tím menší je změna křivky."
• Bézierova křivka řádu vyšší než dva se může protínat nebo mít vrchol pro určité volby kontrolních bodů.

Křivka druhého řádu je parabolický segment

Ekvivalence kvadratické Bézierovy křivky a parabolického segmentu

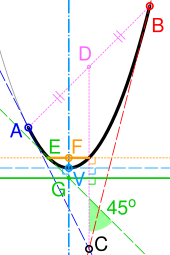
Kvadratická Bézierova křivka je také segmentem paraboly . Protože parabola je kuželosečka , některé zdroje odkazují na kvadratické Béziers jako „kuželosečky“. S odkazem na obrázek vpravo lze odvodit důležité vlastnosti paraboly takto:

1. Tečny k parabole v koncových bodech křivky (A a B) se protínají v jejím řídicím bodě (C).
2. Je-li D středem AB, tečna ke křivce, která je kolmá na CD (přerušovaná azurová čára), definuje její vrchol (V). Jeho osa symetrie (čárkovaná azurová) prochází V a je kolmá na tečnu.
3. E je buď bod na křivce s tečnou 45° k CD (zeleně přerušovaná). Je-li G průsečík této tečny a osy, přímka procházející skrz G a kolmá k CD je směrová přímka (plná zelená).
4. Ohnisko (F) je v průsečíku osy a přímky procházející bodem E a kolmé k CD (žlutě tečkované). Latus rectum je úsečka uvnitř křivky (plná žlutá).

Derivát

Derivace pro křivku řádu n je

${\displaystyle \mathbf {B} '(t)=n\sum _{i=0}^{n-1}b_{i,n-1}(t)(\mathbf {P} _{i+1 }-\mathbf {P} _{i}).}$

Konstrukce Bézierovy křivky

Lineární křivky

T ve funkci pro lineární Bézierovu křivku lze považovat za popis toho , jak daleko je B ( t ) od P ₀ do P ₁ . Například, když t = 0,25, B ( t ) je jedna čtvrtina cesty z bodu P ₀ do P ₁ . Protože se t mění od 0 do 1, _{B (} t ) popisuje čáru od P0 do P1 .

Animace lineární Bézierovy křivky, t v [0,1]

Kvadratické křivky

Pro kvadratické Bézierovy křivky lze sestrojit mezilehlé body Q ₀ a Q ₁ tak, že se t mění od 0 do 1:

• Bod Q ₀ ( t ) se mění od P ₀ do P ₁ a popisuje lineární Bézierovu křivku.
• Bod Q ₁ ( t ) se mění od P ₁ do P ₂ a popisuje lineární Bézierovu křivku.
• Bod B ( t ) je interpolován lineárně mezi Q ₀ ( t ) až Q ₁ ( t ) a popisuje kvadratickou Bézierovu křivku.

Konstrukce kvadratické Bézierovy křivky		Animace kvadratické Bézierovy křivky, t v [0,1]

Křivky vyššího řádu

Pro křivky vyššího řádu je potřeba odpovídajícím způsobem více mezilehlých bodů. Pro kubické křivky lze sestrojit mezilehlé body Q ₀ , Q ₁ a Q ₂ , které popisují lineární Bézierovy křivky, a body R ₀ a R ₁ , které popisují kvadratické Bézierovy křivky:

Konstrukce kubické Bézierovy křivky		Animace kubické Bézierovy křivky, t v [0,1]

Pro křivky čtvrtého řádu lze sestrojit mezilehlé body Q ₀ , Q ₁ , Q ₂ a Q ₃ , které popisují lineární Bézierovy křivky , body R ₀ , R ₁ a R ₂ , které popisují kvadratické Bézierovy křivky , a body S ₀ a S ₁ , které popište kubické Bézierovy křivky:

Konstrukce kvartické Bézierovy křivky		Animace kvartické Bézierovy křivky, t v [0,1]

Pro křivky pátého řádu lze konstruovat podobné mezilehlé body.

Animace Bézierovy křivky pátého řádu, t v [0,1] červeně. Jsou také zobrazeny Bézierovy křivky pro každý z nižších řádů.

Tyto reprezentace spočívají na procesu použitém v De Casteljauově algoritmu k výpočtu Bézierovy křivky.

Offsety (neboli tahy) Bézierovy křivky

Křivka s pevným odsazením od dané Bézierovy křivky, v matematice nazývaná offsetová nebo paralelní křivka (ležící „rovnoběžně“ s původní křivkou, jako offset mezi kolejemi na železniční trati ), nemůže být přesně tvořena Bézierovou křivkou ( kromě některých triviálních případů). Obecně platí, že oboustranná ofsetová křivka kubické Bézierovy křivky je algebraická křivka 10. řádu a obecněji pro Bézierovu křivku stupně n je oboustranná offsetová křivka algebraická křivka stupně 4 n −2. Existují však heuristické metody, které obvykle poskytují adekvátní aproximaci pro praktické účely.

V oblasti vektorové grafiky se malování dvou symetricky vzdálených odsazených křivek nazývá hlazení (Bézierova křivka nebo obecně dráha několika Bézierovských segmentů). Převod z offsetových křivek na vyplněné Bézierovy obrysy má praktický význam při převodu písem definovaných v Metafont , která vyžadují tah Bézierovy křivky, na široce používaná písma PostScript typu 1 , která pouze vyžadují (z důvodů efektivity) matematicky jednodušší ovládání vyplňování obrysu definovaného (neprotínajícími se) Bézierovy křivky.

Stupeň převýšení

Bézierovu křivku stupně n lze převést na Bézierovu křivku stupně n  + 1 se stejným tvarem . To je užitečné, pokud software podporuje Bézierovy křivky pouze určitého stupně. Například systémy, které mohou pracovat pouze s kubickými Bézierovy křivkami, mohou implicitně pracovat s kvadratickými křivkami pomocí jejich ekvivalentní kubické reprezentace.

Pro elevaci stupně použijeme rovnost Každá složka se vynásobí (1 −  t )  at , čímž se stupeň zvýší o jedna, aniž by se změnila hodnota. Zde je příklad zvýšení stupně z 2 na 3. ${\displaystyle \mathbf {B} (t)=(1-t)\mathbf {B} (t)+t\mathbf {B} (t).}$${\displaystyle \mathbf {b} _{i,n}(t)\mathbf {P} _{i}}$

${\displaystyle {\begin{aligned}(1-t)^{2}\mathbf {P} _{0}+2(1-t)t\mathbf {P} _{1}+t^{2} \mathbf {P} _{2}&=(1-t)^{3}\mathbf {P} _{0}+2(1-t)^{2}t\mathbf {P} _{1} +(1-t)t^{2}\mathbf {P} _{2}+(1-t)^{2}t\mathbf {P} _{0}+2(1-t)t^{ 2}\mathbf {P} _{1}+t^{3}\mathbf {P} _{2}\\&=(1-t)^{3}\mathbf {P} _{0}+( 1-t)^{2}t\left(\mathbf {P} _{0}+2\mathbf {P} _{1}\right)+(1-t)t^{2}\left(2 \mathbf {P} _{1}+\mathbf {P} _{2}\right)+t^{3}\mathbf {P} _{2}\\&=(1-t)^{3} \mathbf {P} _{0}+3(1-t)^{2}t{\tfrac {1}{3}}\left(\mathbf {P} _{0}+2\mathbf {P} _{1}\right)+3(1-t)t^{2}{\tfrac {1}{3}}\left(2\mathbf {P} _{1}+\mathbf {P} _{ 2}\right)+t^{3}\mathbf {P} _{2}\end{aligned}}}$

Pro libovolné n používáme rovnosti

${\displaystyle {\begin{cases}{n+1 \choose i}(1-t)\mathbf {b} _{i,n}={n \choose i}\mathbf {b} _{i,n +1}\\{n+1 \vyberte i+1}t\mathbf {b} _{i,n}={n \vyberte i}\mathbf {b} _{i+1,n+1}\ end{cases}}\quad \implies \quad {\begin{cases}(1-t)\mathbf {b} _{i,n}={\frac {n+1-i}{n+1}} \mathbf {b} _{i,n+1}\\t\mathbf {b} _{i,n}={\frac {i+1}{n+1}}\mathbf {b} _{i +1,n+1}\end{cases}}}$

Proto:

${\displaystyle {\begin{aligned}\mathbf {B} (t)&=(1-t)\sum _{i=0}^{n}\mathbf {b} _{i,n}(t) \mathbf {P} _{i}+t\součet _{i=0}^{n}\mathbf {b} _{i,n}(t)\mathbf {P} _{i}\\&= \sum _{i=0}^{n}{\frac {n+1-i}{n+1}}\mathbf {b} _{i,n+1}(t)\mathbf {P} _ {i}+\sum _{i=0}^{n}{\frac {i+1}{n+1}}\mathbf {b} _{i+1,n+1}(t)\mathbf {P} _{i}\\&=\součet _{i=0}^{n+1}\left({\frac {i}{n+1}}\mathbf {P} _{i-1 }+{\frac {n+1-i}{n+1}}\mathbf {P} _{i}\right)\mathbf {b} _{i,n+1}(t)\\&= \sum _{i=0}^{n+1}\mathbf {b} _{i,n+1}(t)\mathbf {P'} _{i}\end{aligned}}}$

zavádějící libovolné a . ${\displaystyle \mathbf {P} _{-1}}$${\displaystyle \mathbf {P} _{n+1}}$

Proto jsou nové kontrolní body

${\displaystyle \mathbf {P'} _{i}={\frac {i}{n+1}}\mathbf {P} _{i-1}+{\frac {n+1-i}{n +1}}\mathbf {P} _{i},\quad i=0,\ldots ,n+1.}$

Opakované elevace stupně

Koncept stupně elevace lze opakovat na řídicím polygonu R , aby se získala sekvence řídicích polygonů R , R ₁ , R ₂ a tak dále. Po r stupňových výškách má polygon R _r vrcholy P _{0, r} , P _{1, r} , P _{2, r} , ..., P _{n + r , r} dané vztahem

${\displaystyle \mathbf {P} _{i,r}=\sum _{j=0}^{n}\mathbf {P} _{j}{\tbinom {n}{j}}{\frac { \tbinom {r}{ij}}{\tbinom {n+r}{i}}}.}$

Lze také ukázat, že pro podkladovou Bézierovu křivku B ,

${\displaystyle \mathbf {\lim _{r\to \infty }R_{r}} =\mathbf {B} .}$

Racionální Bézierovy křivky

Úseky kuželoseček reprezentované přesně racionálními Bézierovy křivkami

Racionální Bézierova křivka přidává nastavitelné závaží, aby poskytla bližší přiblížení libovolným tvarům. Čitatel je vážená Bézierova křivka Bernsteinova tvaru a jmenovatel je vážený součet Bernsteinových polynomů . Racionální Bézierovy křivky lze mimo jiné použít k přesné reprezentaci segmentů kuželoseček , včetně kruhových oblouků.

Je-li dáno n  + 1 kontrolních bodů P ₀ , ..., P _n , lze racionální Bézierovu křivku popsat pomocí

${\displaystyle \mathbf {B} (t)={\frac {\sum _{i=0}^{n}b_{i,n}(t)\mathbf {P} _{i}w_{i} }{\součet _{i=0}^{n}b_{i,n}(t)w_{i}}},}$

nebo jednoduše

${\displaystyle \mathbf {B} (t)={\frac {\sum _{i=0}^{n}{n \choose i}t^{i}(1-t)^{ni}\mathbf {P} _{i}w_{i}}{\součet _{i=0}^{n}{n \choose i}t^{i}(1-t)^{ni}w_{i}} }.}$

Výraz lze rozšířit použitím číselných soustav kromě reálných hodnot pro váhy. V komplexní rovině body {1}, {-1} a {1} s váhami { }, {1} a { } generují úplný kruh s poloměrem jedna. U křivek s body a závažími na kružnici lze váhy škálovat beze změny tvaru křivky. Měřítko centrální váhy výše uvedené křivky o 1,35508 poskytuje jednotnější parametrizaci. ${\displaystyle i}$${\displaystyle -i}$

Aplikace

Počítačová grafika

Bézierova cesta v Adobe Illustratoru

Bézierovy křivky jsou široce používány v počítačové grafice k modelování hladkých křivek. Protože je křivka zcela obsažena v konvexním trupu svých řídicích bodů , lze body graficky zobrazit a použít k intuitivní manipulaci s křivkou. Afinní transformace , jako je translace a rotace , lze aplikovat na křivku aplikací příslušné transformace na řídicí body křivky.

Nejběžnější jsou kvadratické a kubické Bézierovy křivky. Vyhodnocení křivek vyšších stupňů je výpočetně nákladnější . Když jsou potřeba složitější tvary, Bézierovy křivky nízkého řádu se spojí dohromady a vytvoří se složená Bézierova křivka . Složená Bézierova křivka je běžně označována jako „cesta“ v jazycích pro vektorovou grafiku (jako PostScript ), standardech pro vektorovou grafiku (jako SVG ) a programech pro vektorovou grafiku (jako je Artline , Timeworks Publisher , Adobe Illustrator , CorelDraw , Inkscape a Allegro ) . . Aby bylo možné spojit Bézierovy křivky do složené Bézierovy křivky bez zalomení, což je vlastnost nazývaná G1 spojitá , stačí přinutit řídicí bod, ve kterém se setkávají dvě základní Bézierovy křivky, aby ležel na přímce definované dvěma řídicími body na obou stranách.

Abstraktní kompozice kubických Bézierových křivek paprskem sledovaných ve 3D. Průsečík paprsků s rozprostřenými objemy podél křivek je vypočítán pomocí algoritmu Phantom Ray-Hair Intersector.

Nejjednodušší metodou pro převod skenování ( rastrování ) Bézierovy křivky je její vyhodnocení v mnoha těsně rozmístěných bodech a převod skenování aproximující sekvence úseček. To však nezaručuje, že rastrovaný výstup vypadá dostatečně hladce, protože body mohou být od sebe příliš vzdálené. Naopak může generovat příliš mnoho bodů v oblastech, kde je křivka blízko lineární. Běžnou adaptivní metodou je rekurzivní dělení, při kterém se kontrolují kontrolní body křivky, aby se zjistilo, zda se křivka aproximuje přímce v rámci malé tolerance. Pokud ne, křivka se parametricky rozdělí na dva segmenty, 0 ≤ t ≤ 0,5 a 0,5 ≤ t ≤ 1, a stejný postup se použije rekurzivně na každou polovinu. Existují také metody přímého diferencování, ale je třeba věnovat velkou pozornost analýze šíření chyb.

Analytické metody, kde se Bézierova čára protíná každou skenovací linií, zahrnují hledání kořenů kubických polynomů (pro kubické Béziery) a zacházení s více kořeny, takže se v praxi často nepoužívají.

Rasterizační algoritmus použitý v Metafont je založen na diskretizaci křivky, takže je aproximována sekvencí „ tahů věže “, které jsou čistě vertikální nebo čistě horizontální, podél hranic pixelů. Za tímto účelem je rovina nejprve rozdělena na osm 45° sektorů (souřadnicovými osami a dvěma úsečkami ), poté je křivka rozložena na menší segmenty tak, že směr křivkového segmentu zůstane v rámci jednoho sektoru; protože rychlost křivky je polynom druhého stupně, nalezení hodnot, kde je rovnoběžná s jednou z těchto čar, lze provést řešením kvadratických rovnic . V každém segmentu dominuje horizontální nebo vertikální pohyb a celkový počet kroků v obou směrech lze odečíst ze souřadnic koncového bodu; například v sektoru 0–45° dominuje horizontální pohyb doprava, takže zbývá pouze rozhodnout, mezi kterými kroky doprava má křivka udělat krok nahoru. ${\displaystyle y=\pm x}$${\displaystyle t}$

Existuje také modifikovaná forma křivky Bresenhamova algoritmu pro kreslení čar od Zingla, který provádí tuto rastrizaci rozdělením křivky na racionální části a výpočtem chyby v každém umístění pixelu tak, že se buď pohybuje pod úhlem 45°, nebo přímo v závislosti na chybě složení. iteruje přes křivku. To redukuje výpočet dalšího kroku na sérii celočíselných sčítání a odčítání.

Animace

V animačních aplikacích, jako je Adobe Flash a Synfig , se Bézierovy křivky používají k nastínění například pohybu. Uživatelé načrtnou požadovanou cestu v Bézierových křivkách a aplikace vytvoří potřebné rámy, aby se objekt mohl po cestě pohybovat.

Ve 3D animaci se Bézierovy křivky často používají k definování 3D cest a také 2D křivek pro interpolaci klíčových snímků. Bézierovy křivky se nyní velmi často používají k ovládání náběhu animace v CSS , JavaScript , JavaFx a Flutter SDK .

Písma

Písma TrueType používají složené Bézierovy křivky složené z kvadratických Bézierovych křivek. Jiné jazyky a zobrazovací nástroje (jako PostScript , Asymptote , Metafont a SVG ) používají pro kreslení zakřivených tvarů složený Bézierův obraz složený z kubických Bézierovců. Písma OpenType mohou používat oba druhy křivek v závislosti na technologii písma, která je základem obálky OpenType.

Interní vykreslování všech Bézierových křivek v rendererech písma nebo vektorové grafiky je rekurzivně rozdělí až do bodu, kdy je křivka dostatečně plochá, aby mohla být nakreslena jako série lineárních nebo kruhových segmentů. Přesný algoritmus dělení je závislý na implementaci, musí být respektována pouze kritéria rovinnosti pro dosažení potřebné přesnosti a zamezení nemonotónních lokálních změn zakřivení. Funkce "hladká křivka" grafů v aplikaci Microsoft Excel také používá tento algoritmus.

Protože oblouky kružnic a elips nelze přesně znázornit Bézierovými křivkami, jsou nejprve aproximovány Bézierovy křivkami, které jsou zase aproximovány oblouky kružnic. To je neefektivní, protože existují i ​​aproximace všech Bézierových křivek pomocí oblouků kružnic nebo elips, které lze vykreslovat přírůstkově s libovolnou přesností. Jiný přístup, používaný moderními hardwarovými grafickými adaptéry s akcelerovanou geometrií, dokáže převést přesně všechny Bézierovy a kuželové křivky (nebo povrchy) na NURBS , které lze vykreslovat inkrementálně bez předchozího rekurzivního dělení křivky pro dosažení potřebné rovinnosti. Tento přístup také zachovává definici křivky u všech lineárních nebo perspektivních 2D a 3D transformací a projekcí.

Fontové stroje, jako je FreeType , kreslí křivky (a čáry) písma na pixelovaný povrch pomocí procesu známého jako rasterizace písem .

Robotika

Bézierovy křivky mohou být použity v robotice k vytvoření trajektorií koncového efektoru díky schopnosti řídicího polygonu poskytnout jasnou indikaci, zda dráha koliduje s nějakou blízkou překážkou nebo objektem. Kromě toho lze trajektorie kloubního prostoru přesně odlišit pomocí Bézierovy křivky. V důsledku toho se derivace trajektorií kloubního prostoru používají při výpočtu dynamiky a ovládací síly (profily točivého momentu) robotického manipulátoru.

Viz také

• Povrch Bézier
• B-spline
• GEM/4 a GEM/5
• Hermitská křivka
• NURBS
• String art – Bézierovy křivky jsou také tvořeny mnoha běžnými formami strunového umění, kde jsou struny smyčkovány přes rám hřebíků.
• Vlastnost Bézierovy křivky zmenšující odchylky

Poznámky

Reference

Citace

Prameny

Další čtení

• A Primer on Bézierovy křivky  – open source online kniha vysvětlující Bézierovy křivky a související grafické algoritmy s interaktivní grafikou
• Kubické Bezierovy křivky – Pod pokličkou (video)  – video ukazující, jak počítače vykreslují krychlovou Bézierovu křivku, Peter Nowell
• Od Béziera po Bernsteinův sloupec od American Mathematical Society
• "Bézierova křivka" , Encyklopedie matematiky , EMS Press , 2001 [1994]
• Prautzsch, Hartmut; Boehm, Wolfgang; Paluszny, Marco (2002). Bézierovy a B-Spline techniky . Springer Science & Business Media. ISBN 978-3-540-43761-1.
• Gallier, Jean (1999). "Kapitola 5. Polynomiální křivky jako Bézierovy křivky" . Křivky a plochy v geometrickém modelování: Teorie a algoritmy . Morgan Kaufmann.Tato kniha je vyprodaná a je volně dostupná u autora.
• Farin, Gerald E. (2002). Křivky a plochy pro CAGD: Praktický průvodce (5. vydání). Morgan Kaufmann. ISBN 978-1-55860-737-8.
• Weisstein, Eric W. "Bézierova křivka" . MathWorld .
• Hoffmann, Gernot. "Bézierovy křivky" (PDF) . Archivováno z originálu (PDF) dne 2006-12-02.(60 stran)
• Ahn, Young Joon (2004). „Aproximace kruhových oblouků a offsetových křivek pomocí Bézierovy křivky vysokého stupně“ . Journal of Computational and Applied Mathematics . 167 (2): 405–416. Bibcode : 2004JCoAM.167..405A . doi : 10.1016/j.cam.2003.10.008 .
• Davies, Jasone. "Animované Bézierovy křivky" .
• Hovey, Čad (20. května 2022). "Bézierova geometrie" . GitHub .
• Hovey, Čad (2022). Formulace a Python implementace Bézierovy a B-Spline geometrie. SAND2022-7702C . (153 stran)

externí odkazy

Počítačový kód

• TinySpline: Open source C-knihovna pro NURBS, B-splines a Bézierovy křivky s vazbami pro různé jazyky
• Knihovna C++ pro generování Bézierových funkcí v době kompilace
• Jednoduchá implementace Bézierovy křivky pomocí rekurzivní metody v Pythonu