Algebraická křivka - Algebraic curve

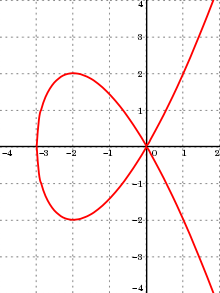
V matematiky , An afinní algebraické rovina křivka je nulový soubor z polynomu ve dvou proměnných. Projektivní algebraická rovina křivka je nulová množina v projektivní rovině jednoho homogenního polynomu ve třech proměnných. Křivku afinní algebraické roviny lze dokončit v projektivní křivce algebraické roviny homogenizací jejího definujícího polynomu. Naopak křivku projektivní algebraické roviny homogenní rovnice h ( x , y , t ) = 0 lze omezit na křivku afinní algebraické rovnice rovnice h ( x , y , 1) = 0 . Tyto dvě operace jsou navzájem inverzní ; proto se často používá fráze křivka algebraické roviny, aniž by bylo výslovně uvedeno, zda se uvažuje o afinním nebo projektivním případě.

Obecněji řečeno, An algebraické křivky je algebraické odrůda o rozměru jednoho. Ekvivalentně je algebraická křivka algebraickou odrůdou, která je birationally ekvivalentní křivce algebraické roviny. Pokud je křivka obsažena v afinním prostoru nebo v projektivním prostoru , lze pro takovou porodní ekvivalenci použít projekci .

Tyto birational ekvivalence redukují většinu studia algebraických křivek na studium křivek algebraických rovin. Některé vlastnosti však nejsou udržovány v porodní ekvivalenci a musí být studovány na neplošných křivkách. To platí zejména pro stupeň a hladkost . Například existují hladké křivky rodu 0 a stupně větší než dva, ale jakákoli rovinná projekce těchto křivek má singulární body (viz vzorec Genus – stupeň ).

Nerovinná křivka se často nazývá prostorová křivka nebo šikmá křivka .

V euklidovské geometrii

Algebraická křivka v euklidovské rovině je množina bodů, jejichž souřadnice jsou řešením bivariační polynomické rovnice p ( x , y ) = 0. Tato rovnice se často nazývá implicitní rovnice křivky, na rozdíl od křivek, které jsou grafem funkce definující výslovně y jako funkci x .

U křivky dané takovou implicitní rovnicí jsou prvními problémy určit tvar křivky a nakreslit ji. Tyto problémy nejsou tak snadno řešitelné jako v případě grafu funkce, pro který lze y snadno vypočítat pro různé hodnoty x . Skutečnost, že definující rovnice je polynom, naznačuje, že křivka má některé strukturní vlastnosti, které mohou pomoci při řešení těchto problémů.

Každá algebraická křivka může být jedinečně rozložena na konečný počet hladkých monotónních oblouků (nazývaných také větve ), někdy spojených některými body, někdy nazývanými „pozoruhodné body“, a případně konečným počtem izolovaných bodů nazývaných acnodes . Hladký monotónní oblouk je graf hladké funkce , která je definována a monotónní na otevřeném intervalu z x v ose. V každém směru je oblouk buď neomezený (obvykle se nazývá nekonečný oblouk ), nebo má koncový bod, který je buď singulárním bodem (to bude definováno níže), nebo bodem s tečnou rovnoběžnou s jednou ze souřadnicových os.

Například pro krychli Tschirnhausen existují dva nekonečné oblouky, jejichž počátek (0,0) je koncovým bodem. Tento bod je jediným singulárním bodem křivky. Existují také dva oblouky, které mají tento singulární bod jako jeden koncový bod a mají druhý koncový bod s horizontální tangens. Nakonec existují dva další oblouky, z nichž každý má jeden z těchto bodů s horizontální tečnou jako prvním koncovým bodem a má jedinečný bod s vertikální tangens jako druhý koncový bod. Naproti tomu sinusoid rozhodně není algebraickou křivkou, která má nekonečný počet monotónních oblouků.

Chcete -li nakreslit algebraickou křivku, je důležité znát pozoruhodné body a jejich tangenty, nekonečné větve a jejich asymptoty (pokud existují) a způsob, jakým je oblouky spojují. Je také užitečné považovat inflexní body za pozoruhodné body. Když jsou všechny tyto informace nakresleny na list papíru, tvar křivky se obvykle zobrazí poměrně jasně. Pokud ne, stačí přidat několik dalších bodů a jejich tangenty, abyste získali dobrý popis křivky.

Metody výpočtu pozoruhodných bodů a jejich tangent jsou popsány níže v části Pozoruhodné body rovinné křivky .

Rovinné projektivní křivky

Často je žádoucí uvažovat o křivkách v projektivním prostoru . Algebraická křivka v projektivní rovině nebo rovině projektivní křivky je množina bodů v projektivní rovině, jejichž projektivními souřadnicemi jsou nuly homogenního polynomu ve třech proměnných P ( x , y , z ).

Každá afinní algebraická křivka rovnice p ( x , y ) = 0 může být doplněna do projektivní křivky rovnice, kde ${\ Displaystyle ^{h} p (x, y, z) = 0,}$

${\ Displaystyle ^{h} p (x, y, z) = z ^{\ deg (p)} p ({\ tfrac {x} {z}}, {\ tfrac {y} {z}})}$

je výsledkem homogenizace z p . Naopak, pokud P ( x , y , z ) = 0 je homogenní rovnice projektivní křivky, pak P ( x , y , 1) = 0 je rovnice afinní křivky, která se skládá z bodů projektivní křivky jehož třetí projektivní souřadnice není nulová. Tyto dvě operace jsou navzájem reciproční, a pokud je p definováno , pak , jakmile homogenní polynom P není dělitelný z . ${\ Displaystyle ^{h} p (x, y, 1) = p (x, y)}$${\ Displaystyle p (x, y) = P (x, y, 1)}$${\ Displaystyle ^{h} p (x, y, z) = P (x, y, z),}$

Například projektivní křivka rovnice x ² + y ² - z ² je projektivní dokončení jednotkové kružnice rovnice x ² + y ² - 1 = 0.

To znamená, že afinní křivka a její projektivní dokončení jsou stejné křivky, nebo přesněji, že afinní křivka je součástí projektivní křivky, která je dostatečně velká na to, aby dobře definovala „úplnou“ křivku. Tento úhel pohledu se běžně vyjadřuje voláním „bodů v nekonečnu“ afinní křivky body (v konečném počtu) projektivního dokončení, které do afinní části nepatří.

Projektivní křivky jsou často studovány pro sebe. Jsou také užitečné pro studium afinních křivek. Například pokud p ( x , y ) je polynom definující afinní křivku, vedle parciálních derivací a je užitečné zvážit derivaci v nekonečnu${\ displaystyle p '_ {x}}$${\ displaystyle p '_ {y}}$

${\ Displaystyle p '_ {\ infty} (x, y) = {^{h} p' _ {z} (x, y, 1)}.}$

Například rovnice tangens afinní křivky rovnice p ( x , y ) = 0 v bodě ( a , b ) je

${\ Displaystyle xp '_ {x} (a, b)+yp' _ {y} (a, b)+p '_ {\ infty} (a, b) = 0.}$

Pozoruhodné body rovinné křivky

V této části považujeme rovinu algebraické křivky definované bivariate polynomu P ( x , y ) a jeho ukončení projektivní, definovanou homogenizaci z p . ${\ Displaystyle P (x, y, z) = {}^{h} p (x, y, z)}$

Křižovatka s čárou

Znát body průsečíku křivky s danou přímkou ​​je často užitečné. Průsečík s osami souřadnic a asymptotami je užitečný pro vykreslení křivky. Průsečík s přímkou ​​rovnoběžnou s osami umožňuje najít alespoň bod v každé větvi křivky. Pokud je k dispozici účinný algoritmus pro hledání kořenů , umožňuje to nakreslit křivku vynesením průsečíku se všemi přímkami rovnoběžnými s osou y a procházející každým pixelem na ose x .

Pokud má polynom definující křivku stupeň d , jakákoli přímka ořízne křivku ve většině d bodů. Bézoutova věta tvrdí, že toto číslo je přesně d , pokud se body hledají v projektivní rovině přes algebraicky uzavřené pole (například komplexní čísla ) a počítají se s jejich multiplicitou . Následující výpočetní metoda tuto větu v tomto jednoduchém případě opět potvrzuje.

Pro výpočet průsečíku křivky definované polynomem p s přímkou ​​rovnice osy + o + c = 0 se řeší rovnice přímky pro x (nebo pro y, pokud a = 0). Nahrazením výsledku v p dostaneme univariační rovnici q ( y ) = 0 (nebo q ( x ) = 0, pokud byla rovnice přímky vyřešena v y ), přičemž každý z jejích kořenů je jednou souřadnicí průsečíku . Druhá souřadnice je odvozena z rovnice přímky. Násobnost průsečíku je násobnost odpovídajícího kořene. Existuje bod průniku v nekonečnu, pokud je stupeň q nižší než stupeň p ; multiplicita takového průsečíku v nekonečnu je rozdílem stupňů p a q .

Tečna v bodě

Tečna v bodě ( a , b ) křivky je rovnicí , jako pro každou diferencovatelnou křivku definovanou implicitní rovnicí. V případě polynomů má jiný vzorec pro tangens jednodušší konstantní člen a je symetrickější: ${\ Displaystyle (xa) p '_ {x} (a, b)+(yb) p' _ {y} (a, b) = 0}$

${\ Displaystyle xp '_ {x} (a, b)+yp' _ {y} (a, b)+p '_ {\ infty} (a, b) = 0,}$

kde je derivace v nekonečnu. Ekvivalence obou rovnic vyplývá z homogenní funkce věta Eulerova aplikován na P . ${\ Displaystyle p '_ {\ infty} (x, y) = P' _ {z} (x, y, 1)}$

Pokud tečna není definována a bod je singulární bod . ${\ Displaystyle p '_ {x} (a, b) = p' _ {y} (a, b) = 0,}$

To se okamžitě rozšíří na projektivní případ: Rovnice tangens v bodě projektivních souřadnic ( a : b : c ) projektivní křivky rovnice P ( x , y , z ) = 0 je

${\ Displaystyle xP '_ {x} (a, b, c)+yP' _ {y} (a, b, c)+zP '_ {z} (a, b, c) = 0,}$

a body křivek, které jsou singulární, jsou body takové, že

${\ Displaystyle P '_ {x} (a, b, c) = P' _ {y} (a, b, c) = P '_ {z} (a, b, c) = 0.}$

(Podmínka P ( a , b , c ) = 0 je implikována těmito podmínkami, Eulerovou větou o homogenní funkci.)

Asymptoti

Každá nekonečná větev algebraické křivky odpovídá bodu na nekonečnu na křivce, tj. Bodu projektivního dokončení křivky, který nepatří do její afinní části. Odpovídající asymptota je tangens křivky v tomto bodě. Může platit obecný vzorec pro tangens k projektivní křivce, ale stojí za to jej v tomto případě jasně uvést.

Nechť je rozklad polynomu definujícího křivku na její homogenní části, kde p _i je součet monomií p stupně i . Z toho vyplývá, že ${\ displaystyle p = p_ {d} +\ cdots +p_ {0}}$

${\ Displaystyle P = {^{h} p} = p_ {d}+zp_ {d-1}+\ cdots+z^{d} p_ {0}}$

a

${\ Displaystyle P '_ {z} (a, b, 0) = p_ {d-1} (a, b).}$

Bod v nekonečnu křivky je nula p tvaru ( a , b , 0). Ekvivalentně ( a , b ) je nula p _d . Základní věta algebry znamená, že přes algebraicky uzavřené oblasti (obvykle pole komplexních čísel), p _d faktory do produktu lineárních faktorů. Každý faktor definuje bod na nekonečnu na křivce: pokud bx  -  ay je takový faktor, pak definuje bod v nekonečnu ( a , b , 0). Přes reals, p _d faktory do lineárních a kvadratických faktorů. Tyto nesnížitelné kvadratické faktory definovat non-real body v nekonečnu, a skutečné body jsou dány lineárními faktory. Pokud ( a , b , 0) je bod v nekonečnu křivky, říká se, že ( a , b ) je asymptotický směr . Nastavení q = p _d rovnice odpovídající asymptoty je

${\ Displaystyle xq '_ {x} (a, b)+yq' _ {y} (a, b)+p_ {d-1} (a, b) = 0.}$

If a asymptota je přímka v nekonečnu a ve skutečném případě má křivka větev, která vypadá jako parabola . V tomto případě se říká, že křivka má parabolickou větev . Li ${\ Displaystyle q '_ {x} (a, b) = q' _ {y} (a, b) = 0}$${\ Displaystyle p_ {d-1} (a, b) \ neq 0,}$

${\ Displaystyle q '_ {x} (a, b) = q' _ {y} (a, b) = p_ {d-1} (a, b) = 0,}$

křivka má singulární bod v nekonečnu a může mít několik asymptot. Mohou být vypočítány metodou výpočtu tečného kužele singulárního bodu.

Singulární body

K singulární body křivky ze studia d definována polynomem p ( x , y ) ze studia d jsou řešení soustavy rovnic:

${\ Displaystyle p '_ {x} (x, y) = p' _ {y} (x, y) = p (x, y) = 0.}$

V charakteristické nule je tento systém ekvivalentní

${\ Displaystyle p '_ {x} (x, y) = p' _ {y} (x, y) = p '_ {\ infty} (x, y) = 0,}$

kde, s notací předchozí části, systémy jsou ekvivalentní Eulerovou homogenní funkční větou . Posledně uvedený systém má tu výhodu, že místo d má svůj třetí polynom stupně d -1 . ${\ Displaystyle p '_ {\ infty} (x, y) = P' _ {z} (x, y, 1).}$

Podobně pro projektivní křivku definovanou homogenním polynomem P ( x , y , z ) stupně d mají singulární body řešení systému

${\ Displaystyle P '_ {x} (x, y, z) = P' _ {y} (x, y, z) = P '_ {z} (x, y, z) = 0}$

jako homogenní souřadnice . (V kladné charakteristice musí být rovnice přidána do systému.) ${\ Displaystyle P (x, y, z)}$

To znamená, že počet singulárních bodů je konečný, pokud p ( x , y ) nebo P ( x , y , z ) je volný čtverec . Bézoutova věta tedy znamená, že počet singulárních bodů je nanejvýš ( d −1) ² , ale tato hranice není ostrá, protože soustava rovnic je předurčena . Pokud jsou povoleny redukovatelné polynomy , ostrá hranice je d ( d −1)/2, této hodnoty je dosaženo, když jsou polynomické faktory v lineárních faktorech, tj. Pokud je křivka spojením d čar. U neredukovatelných křivek a polynomů je počet singulárních bodů nejvýše ( d −1) ( d −2)/2, protože vzorec vyjadřuje rod z hlediska singularit (viz níže). Maximum je dosaženo křivkami rodu nula, jejichž všechny singularity mají multiplicitu dvě a odlišné tangenty (viz níže).

Rovnice tečen v singulárním bodě je dána nenulovou homogenní částí nejnižšího stupně v Taylorově řadě polynomu v singulárním bodě. Když člověk změní souřadnice, aby umístil singulární bod na počátek, rovnice tečen v singulárním bodě je tedy nenulovou homogenní částí nejnižšího stupně polynomu a multiplicita singulárního bodu je stupeň tohoto homogenního část.

Analytická struktura

Studium analytické struktury algebraické křivky v sousedství singulárního bodu poskytuje přesné informace o topologii singularit. Ve skutečnosti je v blízkosti singulárního bodu skutečná algebraická křivka spojením konečného počtu větví, které se protínají pouze v singulárním bodě a vypadají buď jako vrchol nebo jako hladká křivka.

V blízkosti pravidelného bodu může být jedna ze souřadnic křivky vyjádřena jako analytická funkce druhé souřadnice. Toto je důsledek analytické implicitní věty o funkci a znamená to, že křivka je v blízkosti bodu hladká . V blízkosti singulárního bodu je situace komplikovanější a zahrnuje řadu Puiseux , které poskytují analytické parametrické rovnice větví.

Pro popis singularity stojí za to přeložit křivku, která má singularitu na počátku. To se skládá ze změny proměnné formuláře, kde jsou souřadnice singulárního bodu. V následujícím textu je uvažovaný singulární bod vždy považován za počátek. ${\ Displaystyle X = xa, Y = yb,}$${\ displaystyle a, b}$

Rovnice algebraické křivky , kde f je polynom v x a y . Tento polynom lze považovat za polynom v y s koeficienty v algebraicky uzavřeném poli řady Puiseux v x . F tedy může být započítáno do faktorů formy, kde P je řada Puiseux. Tyto faktory jsou všechny různé, pokud f je neredukovatelný polynom , protože to znamená, že f je bez čtverců , což je vlastnost nezávislá na poli koeficientů. ${\ Displaystyle f (x, y) = 0,}$${\ displaystyle yP (x),}$

Série Puiseux, která se zde vyskytuje, má formu

${\ Displaystyle P (x) = \ sum _ {n = n_ {0}}^{\ infty} a_ {n} x^{n/d},}$

kde d je kladné celé číslo a je celé číslo, o kterém lze také předpokládat, že je kladné, protože uvažujeme pouze větve křivky, které procházejí počátkem. Bez ztráty obecnosti můžeme předpokládat, že d je coprime s největším společným dělitelem n tak, že (v opačném případě lze pro exponenty zvolit menšího společného jmenovatele). ${\ displaystyle n_ {0}}$${\ displaystyle a_ {n} \ neq 0}$

Dovolit být primitivní d tý kořen jednoty . Pokud se výše uvedená řada Puiseux vyskytuje při faktorizaci , pak řada d${\ displaystyle \ omega _ {d}}$${\ Displaystyle f (x, y) = 0}$

${\ Displaystyle P_ {i} (x) = \ sum _ {n = n_ {0}}^{\ infty} a_ {n} \ omega _ {d}^{i} x^{n/d}}$

se vyskytují také ve faktorizaci (důsledek Galoisovy teorie ). Tyto řady d jsou zmíněny konjugáty a jsou považovány za jedinou větev křivky indexu rozvětvení d .

V případě skutečné křivky, tj. Křivky definované polynomem se skutečnými koeficienty, mohou nastat tři případy. Pokud žádný nemá skutečné koeficienty, pak má člověk nereálnou větev. Pokud má někdo skutečné koeficienty, může si jej vybrat jako . Pokud d je liché, pak každá skutečná hodnota x poskytuje skutečnou hodnotu a jedna má skutečnou větev, která vypadá pravidelně, i když je singulární, pokud d > 1 . Pokud d je sudé, pak a mají skutečné hodnoty, ale pouze pro x ≥ 0 . V tomto případě skutečná větev vypadá jako vrchol (nebo je vrchol, v závislosti na definici použitého vrcholu). ${\ displaystyle P_ {i} (x)}$${\ displaystyle P_ {i} (x)}$${\ displaystyle P_ {0} (x)}$${\ displaystyle P_ {0} (x)}$${\ displaystyle P_ {0} (x)}$${\ displaystyle P_ {d/2} (x)}$

Například obyčejný hrot má pouze jednu větev. Pokud je definována rovnicí, pak faktorizace je rozvětvený index 2 a dva faktory jsou skutečné a definují každý poloviční větev. Pokud je hrot otočen, stane se z něj rovnice a faktorizace je s (koeficient nebyl zjednodušen na j pro ukázku toho, jak je výše uvedená definice specializována). Index rozvětvení je zde 3 a skutečný je pouze jeden faktor; to ukazuje, že v prvním případě musí být dva faktory považovány za definující stejnou větev. ${\ Displaystyle y^{2} -x^{3} = 0,}$${\ Displaystyle (yx^{3/2}) (y+x^{3/2});}$${\ Displaystyle y^{3} -x^{2} = 0,}$${\ Displaystyle (yx^{2/3}) (yj^{2} x^{2/3}) (y- (j^{2})^{2} x^{2/3}),}$${\ Displaystyle j = (1+{\ sqrt {-3}})/2}$${\ displaystyle (j^{2})^{2}}$${\ displaystyle P_ {i} (x)}$

Nerovinné algebraické křivky

Algebraické křivky je algebraické odrůda o rozměru jednoho. To znamená, že afinní křivka v afinním prostoru dimenze n je definována přinejmenším n -1 polynomy v n proměnných. Chcete-li definovat křivku tyto polynomy musí generovat primární ideál o Krull dimenze 1. Tato podmínka není snadné testu v praxi. Proto může být upřednostňován následující způsob reprezentace neplošných křivek.

Nechť je n polynomů ve dvou proměnných x ₁ a x ₂ tak, že f je neredukovatelné. Body v afinním prostoru dimenze n , jejichž souřadnice splňují rovnice a nerovnice ${\ Displaystyle f, g_ {0}, g_ {3}, \ ldots, g_ {n}}$

${\ displaystyle {\ begin {aligned} & f (x_ {1}, x_ {2}) = 0 \\ & g_ {0} (x_ {1}, x_ {2}) \ neq 0 \\ x_ {3} & = {\ frac {g_ {3} (x_ {1}, x_ {2})} {g_ {0} (x_ {1}, x_ {2})}}} \\ & {} \ \ vdots \\ x_ {n} & = {\ frac {g_ {n} (x_ {1}, x_ {2})} {g_ {0} (x_ {1}, x_ {2})}} \ \ end {aligned}}}$

jsou všechny body algebraické křivky, ve kterých byl odebrán konečný počet bodů. Tato křivka je definována systémem generátorů ideálu polynomů h tak, že existuje celé číslo k , které patří ideálu generovanému . Tato reprezentace je birativní ekvivalencí mezi křivkou a rovinnou křivkou definovanou f . Tímto způsobem lze znázornit každou algebraickou křivku. Může však být zapotřebí lineární změna proměnných, aby téměř vždy byla injektivní projekce na dvě první proměnné. Když je potřeba změna proměnných, je téměř každá změna výhodná, jakmile je definována v nekonečném poli. ${\ displaystyle g_ {0}^{k} h}$${\ Displaystyle f, x_ {3} g_ {0} -g_ {3}, \ ldots, x_ {n} g_ {0} -g_ {n}}$

Tato reprezentace nám umožňuje snadno odvodit jakoukoli vlastnost nerovinné algebraické křivky, včetně jejího grafického znázornění, z odpovídající vlastnosti její rovinné projekce.

Pro křivku definovanou jejími implicitními rovnicemi lze výše uvedenou křivku snadno odvodit z Gröbnerova základu pro uspořádání bloku tak, že blok menších proměnných je ( x ₁ , x ₂ ). Polynom f je jedinečný polynom v základně, který závisí pouze na x ₁ a x ₂ . Zlomky g _i / g ₀ se získají volbou pro i = 3, ..., n polynomu na bázi, která je lineární v x _i a závisí pouze na x ₁ , x ₂ a x _i . Pokud tyto volby nejsou možné, znamená to buď, že rovnice definují algebraickou množinu, která není odrůdou, nebo že odrůda není dimenze jedna, nebo že je třeba změnit souřadnice. Druhý případ nastává, když f existuje a je jedinečný, a pro i = 3, ..., n existují polynomy, jejichž úvodní monomie závisí pouze na x ₁ , x ₂ a x _i .

Algebraická funkční pole

Studium algebraických křivek lze omezit na studium neredukovatelných algebraických křivek: křivek, které nelze zapsat jako spojení dvou menších křivek. Až birational rovnocennosti se nesnížitelné křivky nad polem F jsou kategoricky ekvivalentní k algebraické funkce pole v jedné proměnné nad F . Takový algebraické funkce pole je pole rozšíření K z F , která obsahuje prvek x, který je transcendentní přes F , a tak, že K je konečná algebraické rozšíření F ( x ), která je pole racionálních funkcí v neurčité x nad  F .

Uvažujme například pole C komplexních čísel, přes které může být definováno pole C ( x ) racionálních funkcí v  C . Pokud y ²  =  x ³  -  x  - 1, pak pole C ( x ,  y ) je eliptické funkční pole . Prvek x není jednoznačně určen; pole lze také považovat například za rozšíření C ( y ). Algebraická křivka odpovídající funkčnímu poli je jednoduše množina bodů ( x ,  y ) v C ² splňující y ²  =  x ³  -  x  - 1.

Pokud pole F není algebraicky uzavřené, je pohled na funkční pole o něco obecnější než uvažování locus of points, protože zahrnujeme například „křivky“ bez bodů na nich. Například, pokud je pole báze F je pole R reálných čísel, pak x ²  +  y ²  = -1 definuje algebraické rozšíření pole R ( x ), avšak odpovídající křivka považován za podmnožinu R ² nemá žádné body . Rovnice x ²  +  y ²  = -1 se definují neredukovatelnou algebraické křivky nad R ve schématu smyslu (s integrálem , oddělený jednorozměrné schémata z konečného typu přes R ). V tomto smyslu obecně platí , že korespondence mezi dvěma neredukovatelnými algebraickými křivkami nad F (až do ekvivalence porodu) a algebraickými funkcemi v jedné proměnné nad F obecně platí.

Dvě křivky mohou být birationally ekvivalentní (tj. Mají izomorfní funkční pole), aniž by byly izomorfní jako křivky. Situace se stává snazší, když se zabýváme nonsingulárními křivkami, tj. Těmi , které postrádají jakékoli singularity. Dvě nesingulární projektivní křivky nad polem jsou izomorfní právě tehdy, pokud jsou jejich funkční pole izomorfní.

Tsenova věta je o funkčním poli algebraické křivky nad algebraicky uzavřeným polem.

Složité křivky a skutečné povrchy

Složitá projektivní algebraická křivka spočívá v n -rozměrném komplexním projektivním prostoru CP ⁿ . To má komplexní dimenzi n , ale topologickou dimenzi, jako skutečný rozmanitý , 2 n , a je kompaktní , propojené a orientovatelné . Algebraická křivka nad C má rovněž topologický rozměr dva; jinými slovy, je to povrch .

Tyto topologické rod tohoto povrchu, který je počet držadel nebo koblihy otvory, je rovná geometrické rodu algebraické křivky, která může být vypočítán algebraickými prostředky. Stručně řečeno, pokud vezmeme v úvahu rovinnou projekci nesingulární křivky, která má stupeň d a pouze obyčejné singularity (singularity multiplicity dvě s odlišnými tangenty), pak rod je ( d  - 1) ( d  - 2)/2 -  k , kde k je počet těchto singularit.

Kompaktní povrchy Riemann

Riemann povrch je spojen komplexní analytický potrubí z jednoho celku rozměru, který připojený skutečný potrubí ze dvou rozměrů činí. Je kompaktní, pokud je kompaktní jako topologický prostor.

K dispozici je trojitý ekvivalence kategorií mezi kategorie hladkých nerozložitelné projektivní algebraických křivek nad C (s nekonstantní pravidelných mapy jsou morphisms), kategorii kompaktních Riemann povrchů (s nekonstantní holomorfních mapy jsou morfizmö) a opačný z kategorie algebraických funkčních polí v jedné proměnné nad C (s polními homomorfismy, které fixují C jako morfismy). To znamená, že při studiu těchto tří předmětů v jistém smyslu studujeme jednu a tu samou věc. Umožňuje použít v algebraické geometrii komplexní analytické metody a v obou algebraicko-geometrické metody v komplexní analýze a metody teoretické teorie pole. To je charakteristické pro mnohem širší třídu problémů v algebraické geometrii.

Obecnější teorii viz také algebraická geometrie a analytická geometrie .

Singularity

Pomocí vnitřního konceptu tečného prostoru jsou body P na algebraické křivce C klasifikovány jako hladké (synonymní: nesingulární ) nebo singulární . Vzhledem k n −1 homogenním polynomům v proměnných n +1 můžeme jakobiánskou matici najít jako ( n −1) × ( n +1) matici parciálních derivací. Pokud je hodnost této matice n −1, pak polynomy definují algebraickou křivku (v opačném případě definují algebraickou rozmanitost vyšších dimenzí). Pokud hodnost zůstane n −1, když je jakobiánská matice vyhodnocena v bodě P na křivce, pak je bod hladký nebo pravidelný bod; jinak je to singulární bod . Zejména je -li křivka rovinou projektivní algebraické křivky definovanou jedinou homogenní polynomickou rovnicí f ( x , y , z ) = 0, pak jsou singulárními body přesně body P, kde je hodnost 1 × ( n + 1) matice je nula, tedy kde

${\ Displaystyle {\ frac {\ částečný f} {\ částečný x}} (P) = {\ frac {\ částečný f} {\ částečný y}} (P) = {\ frac {\ částečný f} {\ částečný z}} (P) = 0.}$

Protože f je polynom, je tato definice čistě algebraická a nepředpokládá povahu pole F , které zejména nemusí být skutečná ani komplexní čísla. Mělo by se samozřejmě připomenout, že (0,0,0) není bodem křivky, a tedy ani singulárním bodem.

Podobně pro afinní algebraickou křivku definovanou jedinou polynomickou rovnicí f ( x , y ) = 0, pak jsou singulárními body přesně body P křivky, kde je hodnost 1 × n jakobiánské matice nulová, tj. kde

${\ Displaystyle f (P) = {\ frac {\ částečná f} {\ částečná x}} (P) = {\ frac {\ částečná f} {\ částečná y}} (P) = 0.}$

Singularity křivky nejsou birational invariants. Nalezení a klasifikace singularit křivky je však jedním ze způsobů výpočtu rodu , což je birational invariant. Aby to fungovalo, měli bychom uvažovat o křivce projektivně a požadovat, aby F byla algebraicky uzavřená, takže jsou zohledněny všechny singularity, které ke křivce patří.

Klasifikace singularit

Singulární body zahrnují více bodů, kde křivka přechází nad sebou, a také různé druhy vrcholů , například křivky znázorněné rovnicí x ³  = y ² v (0,0).

Křivka C má nanejvýš konečný počet singulárních bodů. Pokud žádný nemá, lze jej nazvat hladkým nebo nesingulárním . Obvykle je tato definice chápána přes algebraicky uzavřené pole a pro křivku C v projektivním prostoru (tj. Kompletní ve smyslu algebraické geometrie). Rovinná křivka rovnice je například považována za singulární, protože má singulární bod (vrchol) v nekonečnu. ${\ displaystyle yx^{3} = 0}$

Ve zbývající části této části je uvažována rovinná křivka C definovaná jako nulová množina bivariátového polynomu f ( x , y ) . Některé z výsledků, ale ne všechny, mohou být zobecněny na nerovinné křivky.

Singulární body jsou klasifikovány pomocí několika invarianty. Násobnost m je definována jako maximální celé číslo, takže derivace f pro všechny řády až do m - 1 zmizí (také minimální průsečík mezi křivkou a přímkou ​​v P ). Intuitivně singulární bod má delta invariantní , delta , pokud se zaměřuje δ běžných dvojité body v P . Abychom to upřesnili, proces foukání vytváří takzvané nekonečně blízké body a sečtením m ( m −1)/2 přes nekonečně blízké body, kde m je jejich multiplicita, vzniká δ . Pro neredukovatelnou a redukovanou křivku a bod P můžeme definovat δ algebraicky jako délku místa, kde je místní prstenec na P a je jeho integrálním uzavřením. ${\ displaystyle {\ widetilde {{\ mathcal {O}} _ {P}}}/{\ mathcal {O}} _ {P}}$${\ displaystyle {\ mathcal {O}} _ {P}}$${\ displaystyle {\ widetilde {{\ mathcal {O}} _ {P}}}}$

Milnor číslo μ ze singularity je stupeň mapování grad f ( x , y )/| grad  f ( x , y ) |na malé sféře poloměru ε, ve smyslu topologického stupně spojitého mapování , kde grad  f je (komplexní) gradientové vektorové pole f . Vztahuje se k δ a r podle vzorce Milnor – Jung ,

μ = 2δ - r + 1.

Zde větvení číslo r z P je počet lokálně nesnížitelných poboček v P . Například r = 1 při obyčejném vrcholu a r = 2 při obyčejném dvojitém bodě. Násobnost m je alespoň r , a že P je singulární právě tehdy, když m je alespoň 2. δ je navíc alespoň m ( m -1)/2.

Výpočet delta invarianty všech singularit umožňuje určit rod g křivky; pokud d je stupeň, pak

${\ Displaystyle g = {\ frac {1} {2}} (d-1) (d-2)-\ sum _ {P} \ delta _ {P},}$

kde je součet převzat všechny singulární body P komplexní křivky projektivní roviny. Říká se tomu rodová formule .

Přiřaďte invarianty [ m , δ, r ] k singularitě, kde m je multiplicita, δ je invariant delta a r je číslo větvení. Pak obyčejný vrchol je bod s invarianty [2,1,1] a obyčejný dvojitý bod je bod s invarianty [2,1,2] a obyčejný m -vícenásobný bod je bod s invarianty [ m , m ( m -1)/2, m ].

Příklady křivek

Racionální křivky

Racionální křivka , také nazýván unicursal křivka, je jakýkoliv křivka, která je birationally ekvivalentní k vedení, které může mít za projektivní linie; podle toho můžeme identifikovat funkční pole křivky s polem racionálních funkcí v jednom neurčitém F ( x ). Pokud je F algebraicky uzavřený, je to ekvivalentní křivce rodu nula; pole všech skutečných algebraických funkcí definovaných na skutečné algebraické rozmanitosti x ² + y ²  = −1 je pole nulového rodu, které není racionálním funkčním polem.

Konkrétně racionální křivka vložená do afinního prostoru dimenze n nad F může být parametrizována (kromě izolovaných výjimečných bodů) pomocí n racionálních funkcí jednoho parametru t ; redukcí těchto racionální funkce na stejnou jmenovateli n 1 výsledné polynomy definovat polynomiální parametrizace o projektivní ukončení křivky v projektivní prostoru. Příkladem je racionální normální křivka , kde všechny tyto polynomy jsou monomie .

Každá kuželosečka definovaná nad F s racionálním bodem v F je racionální křivka. Lze jej parametrizovat nakreslením čáry se sklonem t skrz racionální bod a průsečíkem s kvadratickou křivkou roviny; to dává polynom s F -racionálními koeficienty a jedním F -racionálním kořenem, proto je druhý kořen také F -racionální (tj. patří do F ).

Uvažujme například elipsu x ² + xy + y ²  = 1, kde (−1, 0) je racionální bod. Nakreslením přímky se sklonem t z (−1,0), y  = t ( x +1), jejím nahrazením v rovnici elipsy, faktoringem a řešením pro x získáme

${\ Displaystyle x = {\ frac {1-t^{2}} {1+t+t^{2}}}.}$

Pak rovnice pro y je

${\ Displaystyle y = t (x+1) = {\ frac {t (t+2)} {1+t+t^{2}}} \ ,,}$

který definuje racionální parametrizaci elipsy, a proto ukazuje, že elipsa je racionální křivka. Jsou uvedeny všechny body elipsy, kromě (−1,1), což odpovídá t  = ∞; celá křivka je proto parametrizována skutečnou projektivní přímkou.

Na takovou racionální parametrizaci lze uvažovat v projektivním prostoru tím, že první projektivní souřadnice přirovnáme k čitatelům parametrizace a poslední ke společnému jmenovateli. Protože je parametr definován v projektivní linii, polynomy v parametru by měly být homogenizovány . Například projektivní parametrizace výše uvedené elipsy je

${\ Displaystyle X = U^{2} -T^{2}, \ quad Y = T \, (T+2 \, U), \ quad Z = T^{2}+TU+U^{2} .}$

Odstraněním T a U mezi těmito rovnicemi získáme opět projektivní rovnici elipsy

${\ Displaystyle X^{2}+X \, Y+Y^{2} = Z^{2},}$

které lze snadno získat přímo homogenizací výše uvedené rovnice.

Mnoho křivek na seznamu křivek Wikipedie je racionálních, a proto mají podobné racionální parametrizace.

Racionální rovinné křivky

Racionální rovinné křivky jsou racionální křivky vložené do . Vzhledem k obecným řezům stupňů homogenních polynomů ve dvou souřadnicích existuje mapa${\ displaystyle \ mathbb {P} ^{2}}$${\ Displaystyle s_ {1}, s_ {2}, s_ {3} \ in \ Gamma (\ mathbb {P} ^{1}, {\ mathcal {O}} (d))}$${\ displaystyle d}$${\ displaystyle x, y}$

${\ Displaystyle s: \ mathbb {P} ^{1} \ to \ mathbb {P} ^{2}}$ dána ${\ Displaystyle s ([x: y]) = [s_ {1} ([x: y]): s_ {2} ([x: y]): s_ {3} ([x: y])]}$

definování racionální rovinné křivky stupně . Ke všem takovým stabilním křivkám patří parametrizovaný prostor modulů (kde je třída hyperplane) . K určení dimenze prostoru modulů lze provést počet dimenzí: Existují parametry udávající celkové parametry pro každou z sekcí. Potom, protože jsou považovány za až projektivní kvocient, je v nich menší parametr . Kromě toho existuje trojrozměrná skupina automorfismů , a proto má rozměr . Tento prostor modulů lze použít k počítání počtu stupňů protínajících se křivek racionálních rovin pomocí Gromov -Wittenovy teorie . Je to dáno rekurzivním vztahem${\ displaystyle d}$ ${\ displaystyle {\ mathcal {M}} = {\ overline {\ mathcal {M}}} _ {0,0} (\ mathbb {P} ^{2}, d \ cdot [H])}$${\ displaystyle [H]}$${\ displaystyle d+1}$${\ displaystyle \ Gamma (\ mathbb {P} ^{1}, {\ mathcal {O}} (d))}$${\ Displaystyle 3d+3}$${\ displaystyle \ mathbb {P} ^{2}}$${\ displaystyle 1}$${\ displaystyle {\ mathcal {M}}}$${\ displaystyle \ mathbb {P} ^{1}}$${\ displaystyle {\ mathcal {M}}}$${\ Displaystyle 3d+3-1-3 = 3d-1}$${\ displaystyle N_ {d}}$${\ displaystyle d}$${\ Displaystyle 3d-1}$

${\ Displaystyle N_ {d} = \ sum _ {d_ {A}+d_ {B} = d} N_ {d_ {A}} N_ {d_ {B}} d_ {A}^{2} d_ {B} \ left (d_ {B} {\ binom {3d-4} {3d_ {A} -2}}-d_ {A} {\ binom {3d-4} {3d_ {A} -1}} \ right)}$

kde . ${\ displaystyle N_ {1} = N_ {2} = 1}$

Eliptické křivky

Eliptické křivky může být definován jako jakákoliv křivce rodu jeden s racionálním bodem : společný model je nonsingular kubická křivka , která postačuje k modelování jakéhokoliv rodu jednu křivku. V tomto modelu je rozlišovací bod běžně považován za inflexní bod v nekonečnu; to odpovídá požadavku, aby křivku bylo možné napsat ve formě Tate-Weierstrass, což je ve své projektivní verzi

${\ Displaystyle y^{2} z+a_ {1} xyz+a_ {3} yz^{2} = x^{3}+a_ {2} x^{2} z+a_ {4} xz^{ 2}+a_ {6} z^{3}.}$

Pokud je charakteristika pole odlišná od 2 a 3, pak lineární změna souřadnic umožňuje vkládání, které dává klasický Weierstrassův tvar ${\ displaystyle a_ {1} = a_ {2} = a_ {3} = 0,}$

${\ Displaystyle y^{2} = x^{3}+px+q.}$

Eliptické křivky nesou strukturu abelianské skupiny s rozlišovacím bodem jako identitou skupinového zákona. V rovinném kubickém modelu se tři body ve skupině sčítají k nule právě tehdy, jsou -li kolineární . Pro eliptickou křivku definovanou v komplexních číslech je skupina izomorfní vůči aditivní skupině komplexního rovinného modulu, periodické mřížky odpovídajících eliptických funkcí .

Průsečík dvou kvadrických ploch je obecně nesingulární křivka rodu jedna a stupně čtyři, a tedy eliptická křivka, má -li racionální bod. Ve zvláštních případech může být průnik buď racionálním singulárním kvartikem, nebo je rozložen v křivkách menších stupňů, které nejsou vždy odlišné (buď krychlová křivka a přímka, nebo dva kužely, nebo kuželovitý a dvě přímky, nebo čtyři přímky) .

Křivky rodu větší než jedna

Křivky rodu větší než jedna se výrazně liší od racionálních i eliptických křivek. Takové křivky definované nad racionálními čísly podle Faltingsovy věty mohou mít pouze konečný počet racionálních bodů a lze na ně pohlížet jako na hyperbolické geometrické struktury. Příkladem jsou hyperelliptické křivky , Kleinova křemenná křivka a Fermatova křivka x ⁿ  +  y ⁿ  = z ^n, když n je větší než tři. Také projektivní rovinné křivky a křivky v poskytují mnoho užitečných příkladů. ${\ displaystyle \ mathbb {P} ^{2}}$${\ Displaystyle \ mathbb {P} ^{1} \ times \ mathbb {P} ^{1}}$

Projektivní rovinné křivky

Rovinné křivky stupně , které lze sestrojit jako mizející lokus generické sekce , mají rod${\ Displaystyle C \ subset \ mathbb {P} ^{2}}$${\ displaystyle k}$${\ Displaystyle s \ in \ Gamma (\ mathbb {P} ^{2}, {\ mathcal {O}} (k))}$

${\ displaystyle {\ frac {(k-1) (k-2)} {2}}}$

které lze vypočítat pomocí kohomologie Coherent sheaf cohomology . Zde je stručný souhrn rodů křivek vzhledem k jejich stupni

${\ displaystyle {\ begin {matrix} {\ text {degree}} & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ {\ text {genus}} & 0 & 0 & 1 & 3 & 6 & 10 & 15 \ end {matrix}}}$

Křivka například definuje křivku rodu, která je hladká, protože diferenciály nemají s křivkou žádné společné nuly. Nepřípadem generického řezu je křivka, která by se podle Bezoutsovy věty měla protínat ve většině bodů, tj. spojení dvou racionálních křivek protínajících se ve dvou bodech. Poznámka je dána mizícím lokusem a je dána mizejícím lokusem . Ty lze nalézt explicitně: bod spočívá v obou if . Obě řešení jsou tedy body takové , které jsou a . ${\ Displaystyle x^{4}+y^{4}+z^{4}}$${\ displaystyle 3}$${\ displaystyle 4x^{3}, 4y^{3}, 4z^{3}}$${\ Displaystyle x (x^{2}+y^{2}+z^{2})}$${\ displaystyle 2}$${\ displaystyle C_ {1} \ cup C_ {2}}$${\ displaystyle C_ {1}}$${\ displaystyle x}$${\ displaystyle C_ {2}}$${\ Displaystyle x^{2}+y^{2}+z^{2}}$${\ displaystyle x = 0}$${\ Displaystyle [0: y: z]}$${\ Displaystyle y^{2}+z^{2} = 0}$${\ Displaystyle [0: 1: -1]}$${\ Displaystyle [0: 1: {\ sqrt {-1}}]}$

Křivky v součinu projektivních čar

Křivka daná zanikajícím lokusem pro , pro , dávejte křivky rodu${\ Displaystyle C \ subset \ mathbb {P} ^{1} \ times \ mathbb {P} ^{1}}$${\ Displaystyle s \ in \ Gamma (\ mathbb {P} ^{1} \ times \ mathbb {P} ^{1}, {\ mathcal {O}} (a, b))}$${\ displaystyle a, b \ geq 2}$

${\ Displaystyle ab-a-b+1}$

které lze zkontrolovat pomocí kohomologie Coherent sheaf cohomology . Pokud pak definují křivky rodu , lze tedy křivku jakéhokoli rodu sestrojit jako křivku v . Jejich rody lze shrnout do tabulky${\ displaystyle a = 2}$${\ Displaystyle 2b-2-b+1 = b-1}$${\ Displaystyle \ mathbb {P} ^{1} \ times \ mathbb {P} ^{1}}$

${\ displaystyle {\ begin {matrix} {\ text {bidegree}} & (2,2) & (2,3) & (2,4) & (2,5) \\ {\ text {genus}} & 1 & 2 & 3 & 4 \ end {matrix}}}$

a pro , to je${\ displaystyle a = 3}$

${\ displaystyle {\ begin {matrix} {\ text {bidegree}} & (3,2) & (3,3) & (3,4) & (3,5) \\ {\ text {genus}} & 2 & 4 & 6 & 8 \ end {matrix}}}$

Viz také

Klasická algebraická geometrie

Moderní algebraická geometrie

Geometrie Riemannových povrchů

Poznámky

Reference

• Brieskorn, Egbert; Knörrer, Horst (2013). Rovinné algebraické křivky . Přeložil Stillwell, Johne. Birkhäuser. ISBN 978-3-0348-5097-1.
• Chevalley, Claude (1951). Úvod do teorie algebraických funkcí jedné proměnné . Matematické průzkumy. 6 . Americká matematická společnost. ISBN 978-0-8218-1506-9.
• Coolidge, Julian L. (2004) [1931]. Pojednání o algebraických křivkách roviny . Dover. ISBN 978-0-486-49576-7.
• Farkaš, HM; Kra, I. (2012) [1980]. Riemannovy povrchy . Absolventské texty z matematiky. 71 . Springer. ISBN 978-1-4684-9930-8.
• Fulton, William (1989). Algebraické křivky: Úvod do algebraické geometrie . Série poznámek k přednáškám z matematiky. 30 (3. vyd.). Addison-Wesley. ISBN 978-0-201-51010-2.
• Gibson, CG (1998). Elementární geometrie algebraických křivek: vysokoškolácký úvod . Cambridge University Press. ISBN 978-0-521-64641-3.
• Griffiths, Phillip A. (1985). Úvod do algebraických křivek . Překlad matematických monografií. 70 (3. vyd.). Americká matematická společnost. ISBN 9780821845370.
• Hartshorne, Robin (2013) [1977]. Algebraická geometrie . Absolventské texty z matematiky. 52 . Springer. ISBN 978-1-4757-3849-0.
• Iitaka, Shigeru (2011) [1982]. Algebraická geometrie: Úvod do Birational Geometry algebraických odrůd . Absolventské texty z matematiky. 76 . Springer New York. ISBN 978-1-4613-8121-1.
• Milnor, John (1968). Jedinečné body komplexních povrchových ploch . Princeton University Press. ISBN 0-691-08065-8.
• Serre, Jean-Pierre (2012) [1988]. Algebraické skupiny a pole tříd . Absolventské texty z matematiky. 117 . Springer. ISBN 978-1-4612-1035-1.
• Kötter, Ernst (1887). „Grundzüge einer rein geometrischen Theorie der algebraischen ebenen Curven“ [Základy čistě geometrické teorie křivek algebraických rovin]. Transakce Královské akademie v Berlíně . - získal cenu akademie 1886