
Jednotlivé trajektorie v modelovém toku obecně vykazují výrazně odlišné chování než trajektorie vycházející ze stejných počátečních podmínek skutečného toku. Důvodem je nevyhnutelné hromadění chyb a nejistot a také citlivá závislost na počátečních podmínkách v jakémkoli realistickém modelu toku. Přesto přitažlivý LCS (jako je nestabilní potrubí sedlového bodu) je pozoruhodně robustní s ohledem na chyby a nejistoty modelování. LCS jsou tedy ideálními nástroji pro validaci modelu a benchmarking
Lagrangeovské koherentní struktury ( LCS ) jsou rozlišené povrchy trajektorií v dynamickém systému, které mají významný vliv na blízké trajektorie v časovém intervalu zájmu. Typ tohoto vlivu se může lišit, ale vždy vytváří koherentní trajektorii, pro kterou podkladový LCS slouží jako teoretický středobod. Při pozorování stopovacích vzorů v přírodě člověk snadno identifikuje koherentní rysy, ale často je zajímavá základní struktura vytvářející tyto rysy.
Jak je znázorněno vpravo, jednotlivé trajektorie trasovače tvořící koherentní vzory jsou obecně citlivé na změny jejich počátečních podmínek a systémových parametrů. Naproti tomu LCS vytvářející tyto vzory trajektorie se ukázaly být robustní a poskytují zjednodušenou kostru celkové dynamiky systému. Robustnost této kostry dělá z LCS ideální nástroje pro validaci modelu, porovnávání modelů a benchmarking. LCS lze také použít pro nyní casting a dokonce i krátkodobé předpovědi vývoje vzorů v komplexních dynamických systémech.
Fyzikální jevy řízené LCS zahrnují plovoucí úlomky, úniky ropy, povrchové driftery a vzory chlorofylu v oceánu; mraky sopečného popela a spory v atmosféře; a souvislé davové vzorce tvořené lidmi a zvířaty.
Zatímco LCS obecně existují v každém dynamickém systému, jejich role při vytváření koherentních vzorů je snad nejsnáze pozorovatelná v proudech tekutin. Níže uvedené obrázky jsou příklady toho, jak různé typy LCS ukrytých v geofyzikálních tocích formují sledovací vzory.
Spirálové víry:
hyperbolické a eliptické LCS
(Paul Scully-Power/NASA)
Teplota povrchu moře v Gulf Stream
Parabolic LCS
(NASA)
Fytoplankton v Agulhasově prstenci
2D eliptický LCS
(NASA/GSFC)
Tornádo z
eliptického LCS Florida Keys 3D (válcové)
(Joseph Golden/NOAA)
Parní prsten z
eliptického LCS Mount Etna 3D (toroidní)
(Tom Pfeiffer [1] )
Obecné definice
Materiálové povrchy

Obrázek 1: Invariantní potrubí v rozšířeném fázovém prostoru, tvořeném vyvíjejícím se povrchem materiálu.
Ve fázovém prostoru a v časovém intervalu zvažte neautonomní dynamický systém definovaný prostřednictvím vývojové mapy , mapující počáteční podmínky do jejich polohy kdykoli . Pokud je vývojová mapa pro každou volbu odlišná , pak pro libovolnou hladkou množinu počátečních podmínek v sadě

![{\ displaystyle {\ mathcal {I}} = [t_ {0}, t_ {1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7c754a3dce189aa23b3fd3df2d2785666384e9c)








![{\ Displaystyle {\ mathcal {M}} = \ {(x, t) \ in {\ mathcal {P}} \ times {\ mathcal {I}} \, \ colon [F_ {t_ {0}}^{ t}]^{-1} (x) \ v {\ mathcal {M}} (t_ {0}) \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0274ca15e373d4c8a1496a3dbf57d1c26f4768bd)
je invariantní potrubí v rozšířeném fázovém prostoru . Pojem výpůjčky z dynamiky tekutin označujeme vyvíjející se časový úsek potrubí jako povrch materiálu (viz obr. 1). Vzhledem k tomu, že jakákoli volba sady počátečních podmínek poskytuje invariantní varietu , invariantní potrubí a jejich přidružené materiálové povrchy jsou v rozšířeném fázovém prostoru hojné a obecně nerozlišitelné. Pouze několik z nich bude fungovat jako jádra souvislých trajektorií.





LCS jako výjimečný povrch materiálu

Obrázek 2a: Hyperbolický LCS (přitahuje červeně a odpuzuje modře) a eliptický LCS (hranice zelených oblastí) v simulaci dvojrozměrné turbulence. (Obrázek: Mohammad Farazmand)
Aby se vytvořil soudržný obrazec, měl by povrch materiálu po celý časový interval vyvíjet trvalé a konzistentní působení na blízké trajektorie . Příklady takové akce jsou přitažlivost, odpuzování nebo střih. V zásadě se kvalifikuje jakákoli dobře definovaná matematická vlastnost, která vytváří koherentní vzorce z náhodně vybraných blízkých počátečních podmínek.


Většinu takových vlastností lze vyjádřit přísnými nerovnostmi . Například nazýváme hmotný povrch přitahující přes interval, pokud jsou všechny dostatečně malé počáteční poruchy přeneseny tokem do ještě menších konečných poruch . V klasické teorii dynamických systémů se invariantní varieta uspokojující takovou přitažlivou vlastnost po nekonečné časy nazývají atraktory . Jsou nejen speciální, ale dokonce i lokálně unikátní ve fázovém prostoru: žádná souvislá rodina atraktorů nemusí existovat.




Naproti tomu v dynamických systémech definovaných v konečném časovém intervalu přísné nerovnosti nedefinují výjimečné (tj. Místně jedinečné) materiálové povrchy. Vyplývá to z kontinuity toku mapy přes . Pokud například materiálový povrch přitahuje všechny blízké trajektorie v časovém intervalu , pak také dostatečně uzavře jiný materiální povrch.





Povrchy přitahujícího, odpuzujícího a střihajícího materiálu jsou tedy nutně skládány na sebe, tj. Vyskytují se v souvislých rodinách. To vede k myšlence hledat LCS v konečných dynamických systémech jako výjimečné materiálové povrchy, které vykazují vlastnost vyvolávající koherenci silněji než kterýkoli ze sousedních povrchů materiálu. Takové LCS, definované jako extrémy (nebo obecněji stacionární povrchy) pro vlastnost koherence konečného času, budou skutečně sloužit jako pozorované středy trajektorických vzorů. Příklady přitahování, odpuzování a stříhání LCS jsou v přímé numerické simulaci 2D turbulence jsou uvedeny na obr. 2a.
LCS vs. klasické invariantní potrubí
Klasické neměnné rozvody jsou neměnné sady v fázového prostoru města s autonomní dynamického systému. Naproti tomu LCS musí být invariantní pouze v rozšířeném fázovém prostoru. To znamená, že i když je podkladový dynamický systém autonomní , LCS systému v průběhu intervalu budou obecně závislé na čase a budou působit jako vyvíjející se kostry pozorovaných koherentních trajektorií. Obrázek 2b ukazuje rozdíl mezi přitahujícím LCS a klasickým nestabilním potrubím sedlového bodu pro vyvíjející se časy v autonomním dynamickém systému.



Obr. 2b: Přitahující LCS je místně nejatraktivnější materiálová linie (invariantní potrubí v rozšířeném fázovém prostoru polohy a času), která funguje jako páteřní křivka deformujících sledovacích vzorů v konečném časovém intervalu. Naproti tomu nestabilní potrubí pevného bodu sedlového typu je neměnná křivka ve fázovém prostoru, která působí jako asymptotický cíl pro sledovací vzory v nekonečných časových intervalech. Obrázek: Mohammad Farazmand.
Objektivita LCS
Předpokládejme, že fázový prostor podkladového dynamického systému je materiální konfigurační prostor kontinua, jako je tekutina nebo deformovatelné těleso. Například pro dynamický systém generovaný nestabilním rychlostním polem

otevřená sada možných poloh částic je prostor pro konfiguraci materiálu. V tomto prostoru jsou LCS hmotné povrchy tvořené trajektoriemi. To, zda je v LCS obsažena trajektorie materiálu, je vlastnost, která je nezávislá na volbě souřadnic, a proto nemůže záviset na pozorovateli. V důsledku toho LCS podléhají požadavku základní objektivity (materiální rámcová indiference) mechaniky kontinua. Objektivita LCS vyžaduje, aby byly invariantní s ohledem na všechny možné změny pozorovatele, tj. Lineární změny souřadnic formuláře


kde je vektor transformovaných souřadnic; je libovolná vlastní ortogonální matice představující rotace závislé na čase; a je libovolný -rozměrný vektor představující časově závislé překlady. V důsledku toho by každá samostatně konzistentní definice nebo kritérium LCS měla být vyjádřitelná z hlediska veličin, které jsou invariantní vůči rámcům. Například
rychlost deformace a spinový tenzor definovaný jako








transformovat pod euklidovskými změnami rámce na veličiny

Euklidovská změna rámce je tedy ekvivalentní transformaci podobnosti pro , a proto je přístup LCS závislý pouze na vlastních číslech a vlastních vektorech automaticky invariantní k rámci. Naproti tomu přístup LCS v závislosti na vlastních hodnotách obecně není invariantní vůči rámci.



Řada množství rámových závislé, jako je například , , , jakož i průměry nebo vlastních hodnot těchto veličin, se běžně používají v heuristické detekci LCS. I když taková množství mohou účinně označovat rysy pole okamžité rychlosti , schopnost těchto veličin zachytit míchání materiálu, transport a koherenci je omezená a v jakémkoli daném rámci a priori neznámá. Jako příklad uvažujme lineární nestabilní pohyb tekutých částic





což je přesné řešení dvojrozměrných Navier – Stokesových rovnic . Kritérium Okubo-Weiss (závislé na snímku) klasifikuje celou doménu v tomto toku jako eliptickou (vířivou), protože platí s odkazem na euklidovskou maticovou normu. Jak je vidět na obr. 3, trajektorie rostou exponenciálně podél rotující čáry a zmenšují se exponenciálně podél další rotující linie. Z věcného hlediska je tedy tok v každém rámci hyperbolický (sedlový).



Obrázek 3: Okamžité proudnice a vývoj trajektorií vycházejících z nitra jedné z nich v lineárním řešení Navier -Stokesovy rovnice. Tento dynamický systém je klasifikován jako eliptický řadou diagnostiky koherence závislé na rámci, jako je například kritérium Okubo – Weiss. (Obrázek: Francisco Beron-Vera)
Vzhledem k tomu, že Newtonova rovnice pro pohyb částic a Navier-Stokesovy rovnice pro pohyb tekutin jsou dobře známé jako závislé na rámci, může se nejprve zdát neintuitivní vyžadovat invariantnost rámců pro LCS, které jsou složeny z řešení těchto rámcových závislých rovnic. Připomeňme však, že Newtonova a Navierova -Stokesova rovnice představují objektivní fyzikální principy pro trajektorie hmotných částic . Dokud jsou tyto rovnice správně transformovány z jednoho rámce do druhého, generují v novém rámci fyzicky stejné trajektorie materiálu. Ve skutečnosti se rozhodujeme, jak transformovat pohybové rovnice z -rámce na -rám pomocí změny souřadnic, přesně tak, že budeme tvrdit, že trajektorie jsou mapovány do trajektorií, tj. Tím, že budeme muset platit po celou dobu. Časová diferenciace této identity a substituce do původní rovnice v -rámci pak poskytne transformovanou rovnici v -rámci. Tento proces sice přidává do pohybových rovnic nové termíny (setrvačné síly), ale tyto setrvačné termíny vznikají právě proto, aby byla zajištěna neměnnost trajektorií materiálu. LCS, plně složené z materiálových trajektorií, zůstávají neměnné v transformované pohybové rovnici definované v referenčním rámci. V důsledku toho musí být každá self-konzistentní definice nebo metoda detekce LCS také invariantní vůči rámcům.







Hyperbolické LCS

Obrázek 4. Přilákání a odpuzování LCS v rozšířeném fázovém prostoru dvojrozměrného dynamického systému.
Motivováno výše uvedenou diskusí, nejjednodušší způsob, jak definovat přitahující LCS, je požadavek, aby to byl lokálně nejsilnější povrch přitahující materiál v rozšířeném fázovém prostoru (viz obr. 4). Podobně
odpuzující LCS lze definovat jako lokálně nejsilnější povrch odpuzujícího materiálu. Přitahování a odpuzování LCS dohromady se obvykle označuje jako hyperbolické LCS , protože poskytují konečnou generalizaci klasického konceptu normálně hyperbolických invariantních variet v dynamických systémech .

Diagnostický přístup: hřebeny Lyapunovova exponentu (FTLE) konečného času
Heuristicky lze hledat počáteční polohy odpuzujících LCS jako soubor počátečních podmínek, při kterých nekonečně malé odchylky na trajektorie začínající místně rostou nejvyšší rychlostí ve srovnání s trajektoriemi začínajícími . Heuristickým prvkem je, že místo konstrukce vysoce odpuzujícího povrchu materiálu člověk jednoduše hledá body velké separace částic. Takové oddělení může být dobře způsobeno silným smykem podél takto identifikovaných bodů; tato sada vůbec nezaručuje normální odpuzování na blízkých trajektoriích.



Růst nekonečně malé poruchy podél trajektorie se řídí gradientem mapy toku . Nechť je malá odchylka od počátečního stavu s , a s označením libovolného jednotkového vektoru v . Tato porucha obecně roste po trajektorii do poruchového vektoru . Potom lze maximální relativní roztažení nekonečně malých poruch v bodě vypočítat jako












kde označuje
správný tenzor Cauchy – Green tenzoru . Poté dospějeme k závěru, že maximální relativní roztažení zaznamenané podél trajektorie začínající od je spravedlivé . Vzhledem k tomu, že toto relativní roztažení má tendenci rychle růst, je pohodlnější pracovat s jeho růstovým exponentem , který je pak přesně konečným Lyapunovovým exponentem (FTLE)
![{\ Displaystyle C_ {t_ {0}}^{t_ {1}} = \ left [\ nabla F_ {t_ {0}}^{t_ {1}} \ right]^{T} \ nabla F_ {t_ { 0}}^{t_ {1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a4234dd0b40860545b2cc78e272d9ddaf30748)




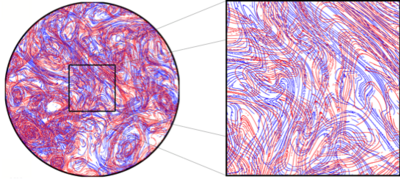
Obrázek 5a. Přitahování (červené) a odpuzující (modré) LCS extrahované jako hřebeny FTLE z dvourozměrného turbulenčního experimentu (Obrázek: Manikandan Mathur)
Proto se očekává, že hyperbolické LCS se objeví jako kodimension-one lokální maximalizující povrchy (nebo hřebeny ) pole FTLE. Toto očekávání se ve většině případů ukazuje jako oprávněné: časové polohy odpuzujících LCS jsou označeny hřebeny . Použitím stejného argumentu ve zpětném čase získáme, že časové polohy přitahujících LCS jsou označeny hřebeny zpětného pole FTLE .




Klasickým způsobem výpočtu Lyapunovových exponentů je řešení lineární diferenciální rovnice pro linearizovanou mapu toku . Vhodnější způsob je vypočítat pole FTLE z jednoduché aproximace konečných rozdílů na deformační gradient. Například v trojrozměrném toku spouštíme trajektorii z jakéhokoli prvku mřížky počátečních podmínek. Pomocí zobrazení souřadnic pro vyvíjející se trajektorii aproximujeme gradient mapy toku jako







Obrázek 5b. Přitahují (modré) a odpuzující (červené) LCS extrahované jako hřebeny FTLE z dvojrozměrné simulace von Karmanovy vírové ulice (Obrázek: Jens Kasten)
s malým vektorem směřujícím ve směru souřadnic. Pro dvojrozměrné toky je relevantní pouze první vedlejší matice výše uvedené matice.




Obrázek 6. Hřebeny FTLE zvýrazňují jak hyperbolické LCS, tak střihové materiálové linie, jako jsou hranice koryta v 3D modelu New River Inlet, Onslow, Severní Karolína (Obrázek: Allen Sanderson).
Problémy s odvozováním hyperbolických LCS z hřebenů FTLE
Hřebeny FTLE se ukázaly být jednoduchým a efektivním nástrojem pro vizualizaci hyperbolických LCS v řadě fyzických problémů, čímž se získají zajímavé obrazy počátečních poloh hyperbolických LCS v různých aplikacích (viz např. Obr. 5a-b). Hřebeny FTLE získané přes posuvná časová okna však netvoří materiálové povrchy. Hřebeny pod proměnlivými tedy nelze použít k
definování Lagrangeových objektů, jako jsou hyperbolické LCS. Místně nejsilnější odpuzující povrch materiálu obecně nebude hrát stejnou roli, a proto jeho vyvíjející se poloha v čase nebude hřebenem . Někteří autoři však s LCS identifikovali široce se vyvíjející hřebeny FTLE druhých derivací vypočítané v klouzavých intervalech formy . Na podporu této identifikace se také často tvrdí, že tok materiálu přes takové hřebeny FTLE s posuvným oknem by měl být nutně malý.
![{\ displaystyle [t_ {0}+T, t_ {1}+T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9a619d4eb2db184073ec4bbda335766512d0a10)


![[t_0, t_1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)
![{\ displaystyle [t_ {0}+T, t_ {1}+T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9a619d4eb2db184073ec4bbda335766512d0a10)


![{\ displaystyle [t_ {0}+T, t_ {1}+T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9a619d4eb2db184073ec4bbda335766512d0a10)
Identifikace „FTLE hřeben = LCS“ však trpí následujícími koncepčními a matematickými problémy:
- Hřebeny FTLE druhé derivace jsou nutně přímky, a proto ve fyzických problémech neexistují.
- Hřebeny FTLE počítané v klouzavých časových oknech s proměnlivými obecně
nejsou lagraniánské a tok jimi obecně není malý.![{\ displaystyle [t_ {0}+T, t_ {1}+T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9a619d4eb2db184073ec4bbda335766512d0a10)
 Zejména široce odkazovaný vzorec toku materiálu pro hřebeny FTLE je nesprávný , dokonce i pro přímé hřebeny FTLE
Hřebeny FTLE označují hyperbolické polohy LCS, ale také zvýrazňují povrchy s vysokým střihem. V aplikacích často vzniká spletitá směs obou typů povrchů (příklad viz obr. 6).
Existuje několik dalších typů LCS (eliptických a parabolických) za hyperbolickými LCS zvýrazněnými hřebeny FTLE
Zejména široce odkazovaný vzorec toku materiálu pro hřebeny FTLE je nesprávný , dokonce i pro přímé hřebeny FTLE
Hřebeny FTLE označují hyperbolické polohy LCS, ale také zvýrazňují povrchy s vysokým střihem. V aplikacích často vzniká spletitá směs obou typů povrchů (příklad viz obr. 6).
Existuje několik dalších typů LCS (eliptických a parabolických) za hyperbolickými LCS zvýrazněnými hřebeny FTLE
Místní variační přístup: Smršťovací a napínací povrchy
Místní variační teorie hyperbolických LCS staví na své původní definici jako nejsilnější odpuzující nebo odpuzující materiálové povrchy v toku v časovém intervalu . V počáteční teplotou , ať
znamenají jednotku kolmo k počáteční povrchu materiálu (viz obr. 6). O neměnnosti hmotných linky,
tečný prostor je mapován do tangenty prostoru ze
strany mapy linearizovaného toku . Současně obraz normálního normálu pod obecně nezůstává normální . Proto kromě normální složky délky rozvíjí advekovaná normála také tangenciální složku délky (srov. Obr. 7).
![[t_0, t_1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)












Obrázek 7. Linearizovaná geometrie toku podél povrchu vyvíjejícího se materiálu.
Pokud , pak se vyvíjející se povrch materiálu přísně odpuzuje blízké trajektorie do konce časového intervalu . Podobně
signály, které přísně přitahují blízké trajektorie podél svých normálních směrů.
Odpuzující (přilákání) LCS v intervalu může být definován jako povrch materiálu , jehož síť odpuzování je bodově maximal (minimální) s ohledem na odchylkách původní normální vektorového pole . Stejně jako dříve označujeme souhrnné odpuzování a přitahování LCS jako hyperbolické LCS .


![[t_0, t_1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)


![[t_0, t_1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)



Řešení těchto lokálních extrémních principů pro hyperbolické LCS ve dvou a třech dimenzích poskytuje jednotku normálních vektorových polí, ke kterým by hyperbolické LCS měly být všude tečné. Existence takových normálních povrchů také vyžaduje podmínku integrability typu Frobenius v trojrozměrném případě. Všechny tyto výsledky lze shrnout následovně:
Hyperbolické podmínky LCS z lokální variační teorie v dimenzích n = 2 a n = 3
| LCS
|
Normální vektorové pole pro 
|
ODE pro n = 2
 |
PDE typu Frobenius pro n = 3
 |
| Přitahování
|
 |
 ( natahovací čáry ) ( natahovací čáry ) |
 ( strečové povrchy ) ( strečové povrchy )
|
| Odpuzování
|

|
 ( zmenšit řádky ) ( zmenšit řádky )
|
 ( smršťovací povrchy ) ( smršťovací povrchy )
|
Odpuzující LCS se získávají jako většina odpuzujících smršťovacích čar, počínaje místními maximy . Atraktivní LCS jsou získány jako nejatraktivnější úseky, počínaje místními minimy . Tyto výchozí body slouží jako počáteční polohy výjimečných trajektorií sedlového typu v toku. Příklad místního variačního výpočtu odpuzujícího LCS je uveden v FIg. 8. Výpočtový algoritmus je k dispozici v nástroji LCS.


Ve 3D toky je namísto řešení Frobenius PDE (viz tabulka výše) pro hyperbolické LCS jednodušší přístup sestrojit průsečíky hyperbolických LCS s vybranými 2D rovinami a numericky přizpůsobit povrch velkému počtu takových křivek průsečíků. Označme jednotku normální z 2D rovině strany . Průsečíková křivka 2D odpuzujícího povrchu LCS s rovinou je kolmá k oběma a k normálovému měřítku LCS. V důsledku toho ODE splňuje průsečná
křivka






jehož trajektorie označujeme jako zmenšené smršťovací linie . (Přesně řečeno, tato rovnice není obyčejnou diferenciální rovnicí, protože její pravá strana není vektorové pole, ale směrové pole, které obecně není globálně orientovatelné). Průsečíky hyperbolických LCS s nejrychlejšími smršťovacími zmenšujícími se liniemi. Určení takových smršťovacích čar v hladké rodině blízkých rovin, potom přizpůsobení povrchu k takto získané rodině křivek poskytuje numerickou aproximaci 2D odpuzujícího LCS.


Globální variační přístup: smršťovací a natahovací linie jako nulová geodetika
Obecný povrch materiálu zažívá ve své deformaci střih a napětí, přičemž oba kontinuálně závisí na počátečních podmínkách na kontinuitě mapy . Zprůměrované napětí a střih uvnitř pásu uzavřených linií materiálu proto typicky vykazují variace uvnitř takového pásu. Dvourozměrná
geodetická teorie LCS hledá výjimečně koherentní místa, kde tento obecný trend selže, což má za následek řádově menší variabilitu ve smyku nebo deformaci, než se běžně očekává přes pás. Geodetická teorie konkrétně hledá LCS jako speciální materiálové linie, kolem nichž materiálové pásy nevykazují žádnou variabilitu ani v průměrném smyku materiálové linie ( Shearless LCSs ), ani v průměrném kmenu materiálové linie ( napínavé nebo eliptické LCS ). Ukázalo se, že takové LCS jsou nulové geodetiky příslušných metrických tenzorů definovaných deformačním polem-odtud název této teorie.






Shearless LCSs se zjistí, že je nulový geodetiky příslušníky Lorentzian metrický tensor je definován jako

![{\ displaystyle D_ {t_ {0}}^{t_ {1}} (x_ {0}) = {\ frac {1} {2}} \ left [C_ {t_ {0}}^{t_ {1} } (x_ {0}) \ Omega -\ Omega C_ {t_ {0}}^{t_ {1}} (x_ {0}) \ right], \ qquad \ Omega = {\ begin {pmatrix} 0 & -1 \\ 1 a 0 \\\ end {pmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c77b4aed7311063d0230c05d58d13d7a0cf0afdc)
Taková nulová geodetika může být prokázána jako tenzorové linie tenzoru Cauchy – Greenova napětí, tj. Jsou tečné ke směrovému poli tvořenému poli vlastních vektorů napětí . Konkrétně,
odpuzující LCSs jsou trajektorie od lokálních maxim na vlastních čísel pole. Podobně přitahování LCS jsou trajektorie vycházející z místních minim v poli vlastní hodnoty. To souhlasí se závěrem místní variační teorie LCS. Geodetický přístup však také vrhá více světla na robustnost hyperbolických LCS: hyperbolické LCS převládají pouze jako stacionární křivky průměrné smykové funkční ve variantách, které nechávají své koncové body pevné. To je v kontrastu s parabolickými LCS (viz níže), které jsou také LCS bez střihu, ale převládají jako stacionární křivky pro smykové funkční i při libovolných variacích. V důsledku toho jsou jednotlivé trajektorie objektivní a prohlášení o koherentních strukturách, které tvoří, by měla být také objektivní.





Ukázka aplikace je znázorněna na obr. 9, kde náhlý výskyt hyperbolického jádra (nejsilnější přitahující část úsečky) uvnitř ropné skvrny způsobil pozoruhodnou nestabilitu Tiger-Tail ve tvaru ropné skvrny.
Eliptické LCS
Elliptc LCS jsou uzavřené a vnořené materiálové povrchy, které fungují jako stavební kameny Lagrangeových ekvivalentů vírů, tj. Rotačních oblastí trajektorií, které obecně procházejí fázovým prostorem bez podstatného roztahování nebo skládání. Napodobují chování tormů Kolmogorov – Arnold – Moser (KAM), které tvoří eliptické oblasti v hamiltonovských systémech . K soudržnosti lze přistupovat buď prostřednictvím jejich homogenní rotace materiálu, nebo prostřednictvím jejich homogenních natahovacích vlastností.
Soudržnost otáčení z úhlu polárního otáčení (PRA)
Jako nejjednodušší přístup k rotační koherenci lze definovat eliptický LCS jako povrch trubkovitého materiálu, podél kterého malé objemy materiálu dokončují stejnou čistou rotaci v průběhu časového intervenčního zájmu. Problém v tom, že v každém prvku objemu materiálu všechna jednotlivá materiálová vlákna (tečné vektory k trajektoriím) provádějí různé rotace.
![[t_ {0}, t_ {1}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)
K získání dobře definované objemové rotace pro každý materiálový prvek lze použít jedinečné levé a pravé polární rozložení gradientu toku ve formě

kde správný ortogonální tenzor se nazývá tenzor rotace a symetrický, pozitivní definitivní tenzory se nazývají tenzor levého roztažení a tenzor pravého roztažení .


Protože tenzor tenzoru Cauchy – Green lze zapsat jako
![{\ Displaystyle C_ {t_ {0}}^{t_ {1}} = [\ nabla F_ {t_ {0}}^{t_ {1}}]^{T} \ nabla F_ {t_ {0}}^ {t_ {1}} = U_ {t_ {0}}^{t_ {1}} U_ {t_ {0}}^{t_ {1}} = V_ {t_ {0}}^{t_ {1}} V_ {t_ {0}}^{t_ {1}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5caee8f36db09843a43a2a1236597fd6b2ad9154)
místní namáhání materiálu popsané vlastními hodnotami a vlastními vektory jsou plně zachyceny singulárními hodnotami a singulárními vektory tahových tenzorů. Zbývající faktor v deformačním gradientu je reprezentován , interpretován jako objemová rotační složka tělesa objemových prvků. V rovinných pohybech je tato rotace definována vzhledem k normálu roviny. Ve třech rozměrech je rotace definována vzhledem k ose definované vlastním vektorem odpovídající jeho jednotkové vlastní hodnotě. U toků vyšší dimenze nelze na tenzor rotace pohlížet jako na rotaci kolem jedné osy.



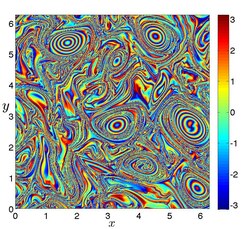
Obrázek 10a. Eliptické LCS odhalené křivkami uzavřené úrovně distribuce PRA v simulaci dvojrozměrné turbulence. (Obrázek: Mohammad Farazmand)

Obrázek 10b. Eliptické LCS odhalené uzavřenými hladinovými křivkami distribuce PRA v ustáleném
toku ABC . (Obrázek: Mohammad Farazmand)
Ve dvou a třech dimenzích tedy existuje polární úhel otočení (PRA), který charakterizuje rotaci materiálu generovanou pro objemový prvek se středem v počátečních podmínkách . Tato PRA je dobře definována až do násobků . U dvojrozměrných toků lze PRA vypočítat z invarianty použití vzorců






které poskytnou čtyřkvadrantovou verzi PRA podle vzorce
![{\ Displaystyle \ theta _ {t_ {0}}^{t} = \ left [1-{\ rm {sign \,}} \ left (\ sin \ theta _ {t_ {0}}^{t} \ vpravo) \ vpravo] \ pi +{\ rm {znak \,}} \ vlevo (\ sin \ theta _ {t_ {0}} ^{t} \ right) \ cos ^{-1} \ left (\ cos \ theta _ {t_ {0}}^{t} \ right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ab9954ea838550ba7d06fdc58b86bd2690c4fca)
U trojrozměrných toků lze PRA opět vypočítat z invarianty ze vzorců


kde je symbol Levi-Civita , je vlastní vektor odpovídající jednotkovému vlastnímu vektoru matice .


![{\ Displaystyle \ left [K_ {t_ {0}}^{t} \ right] _ {jk} = \ left \ langle \ xi _ {j}, \ nabla F_ {t_ {0}}^{t_ {1 }} \ xi _ {k} \ vpravo \ rangle /{\ sqrt {\ lambda _ {k}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a32d1f98355ad4ac1f6303141bc3b1163833f63)
Časové polohy eliptických LCS jsou vizualizovány jako sady tubulárních úrovní distribuce PRA . Ve dvou dimenzích jsou tedy (polární) eliptické LCS jednoduše uzavřenými křivkami úrovně PRA, které se ukazují jako objektivní. Ve třech rozměrech jsou (polární) eliptické LCS toroidní nebo válcové povrchové plochy PRA, které však nejsou objektivní, a proto se v rotujících rámcích obecně mění. Koherentní Lagrangeovy hranice vírů lze zobrazit jako nejvzdálenější členy vnořených rodin eliptických LCS. Dvourozměrné a trojrozměrné příklady eliptických LCS odhalené povrchy PRA trubkovitých úrovní jsou znázorněny na obr. 10a-b.


Rotační soudržnost z Lagrangeově průměrované odchylky vorticity (LAVD)
Sady úrovní PRA jsou objektivní ve dvou dimenzích, ale ne ve třech dimenzích. Dalším nedostatkem tenzoru polární rotace je její dynamická nekonzistence: polární rotace vypočítané v sousedních dílčích intervalech celkové deformace se nesčítají s rotací vypočítanou pro plný časový interval stejné deformace. I když je tedy tenzor rotace nejbližší pevnému časovému intervalu v normě v pevném časovém intervalu , nevytvářejí po částech nejvhodnější rotace tuhého tělesa a jsou různé. Z tohoto důvodu se rotace předpovídané tenzorem polární rotace v různých časových intervalech odklání od experimentálně pozorované střední rotace materiálu tekutých prvků.



![{\ displaystyle [t_ {0}, t_ {1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)



Obrázek 11a: Rotačně koherentní mezoskálové vířivé hranice v oceánu v čase t0 = 11. listopadu 2006, identifikované ze satelitních povrchových rychlostí pomocí integračního času t1-t0 = 90 dní. Hranice jsou identifikovány jako nejvzdálenější uzavřené obrysy LAVD s malým nedostatkem konvexity. Na pozadí je také zobrazen obrysový graf pole LAVD pro referenci. (Obrázek: Alireza Hadjighasem)
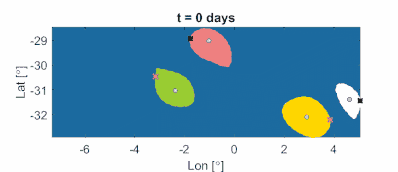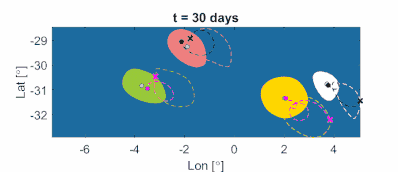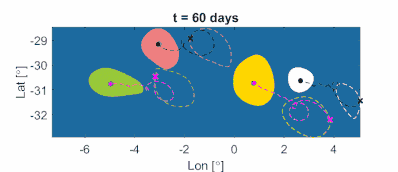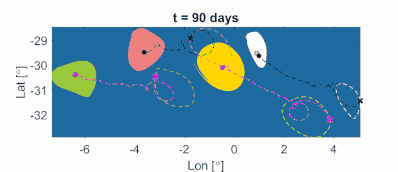
Obrázek 11b: Materiálně advekčně rotované koherentní mezoskálové vířivé hranice a vířivá centra v oceánu spolu s reprezentativními trajektoriemi inerciálních částic inicializovanými na vířivých hranicích. Vířivá centra jsou získána jako lokální maxima pole LAVD. Jak lze matematicky dokázat, těžké částice (azurové) konvergují do center anticyklonických (ve směru hodinových ručiček) vírů. Částice světla (černé) konvergují do center cyklónových (pravotočivých) vírů. (Film: Alireza Hadjighasem)
Alternativa ke klasickému polárnímu rozkladu poskytuje řešení problému neobjektivity i dynamické nekonzistence. Konkrétně je ve formě také dynamický polární rozklad (DPD) deformačního gradientu

kde správné ortogonální tenzor je
dynamická rotace tensor a non-singulární tensors jsou levá dynamické úsek tensor a hned dynamický stretch tensor , resp. Stejně jako klasický polární rozklad platí DPD v jakékoli konečné dimenzi. Na rozdíl od klasického polárního rozkladu jsou ale tenzory dynamické rotace a roztažení získány z řešení lineárních diferenciálních rovnic, nikoli z maticových manipulací. Zejména je to deformační gradient čistě rotačního toku




a je deformačním gradientem čistě napínacího toku


.
Tenzor dynamické rotace lze dále rozložit na dva deformační gradienty: jeden pro prostorově rovnoměrné (tuhé těleso) otáčení a druhý, který se od tohoto rovnoměrného otáčení odchyluje:


Jako prostorově nezávislá rotace tuhého tělesa je správný ortogonální tenzor relativní rotace dynamicky konzistentní a slouží jako deformační gradient relativního rotačního toku

![{\ Displaystyle {\ dot {\ alpha}} = \ left [W \ left (x (t; x_ {0}), t \ right)-{\ bar {W}} \ left (t \ right) \ right ] \ alpha.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d4ca1677536cdf0c5d9d7f2c462885bf06563a7)
Naproti tomu správný ortogonální tenzor střední rotace je deformační gradient toku střední rotace


Dynamická konzistence znamená, že celkový úhel přehnutý kolem vlastní osy otáčení je dynamicky konzistentní. Tento vnitřní úhel otočení je také objektivní a ukazuje se, že se rovná jedné polovině Lagrangeově zprůměrované odchylky vorticity ( LAVD ). LAVD je definována jako velikost průměrné odchylky vorticity od trajektorie od jejího prostorového průměru. S vířivostí a jejím prostorovým průměrem





LAVD v časovém intervalu má tedy formu
![[t_0, t_1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)

s označením (případně časově proměnné) oblasti definice rychlostního pole . Tento výsledek platí jak ve dvou, tak ve třech rozměrech, a umožňuje výpočet dobře definovaného, objektivního a dynamicky konzistentního úhlu rotace materiálu podél jakékoli trajektorie.



Obrázek 11c: Rotačně koherentní mezoskálová vířivá (žlutá) v oceánském modelu South Ocean State Estimate (SOSE) v čase t0 = 15. května 2006, počítáno jako trubkovitý povrch na úrovni LAVD po dobu t1-t0 = 120 dní. Rovněž jsou ukázány blízké povrchy na úrovni LAVD, které ilustrují rotační nesoudržnost mimo vír. (Obrázek: Alireza Hadjighasem)
Nejvzdálenější komplexní tubulární hladinové křivky LAVD definují počáteční polohy rotačně koherentních hranic víru materiálu v dvojrozměrných nestabilních tocích (viz obr. 11a). Konstrukčně mohou tyto hranice vykazovat příčné filamentace, ale jakékoli vyvíjející se vlákno se stále otáčí s hranicí, aniž by globální příčný odchod tvořil materiální vír. (Výjimkou jsou nevidomé toky, kde je možné takové globální opuštění povrchů na úrovni LAVD z víru, protože tekuté prvky si po celou dobu zachovávají rychlost rotace materiálu). Je pozoruhodné, že centra rotačně koherentních vírů (definovaných lokálními maximy pole LAVD) mohou být prokázána jako pozorovaná centra přitažlivosti nebo odpudivosti pro pohyb částic konečné velikosti (inerciální) v geofyzikálních tocích (viz obr. 11b). V trojrozměrných proudech definují povrchy tubulárních hladin LAVD počáteční polohy dvourozměrných vířivých hraničních povrchů (viz obr. 11c), které zůstávají rotačně koherentní v časovém intcentru | ervalu (viz obr. 11d).
![{\ displaystyle [t_ {0}, t_ {1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)

Obr. 11c Materiálová advekce rotačně soudržného Lagrangeova víru a jeho jádra v datové sadě 3D SOSE modelu. (Animace: Alireza Hadjighasem)
Soudržnost založená na protahování z místního variačního přístupu: smykové povrchy
Místní variační teorie eliptických LCS se zaměřuje na materiálové povrchy, které lokálně maximalizují střih materiálu v konečném časovém intervalu, který nás zajímá. To znamená, že v počátečním bodě každého bodu eliptického LCS je tečný prostor rovinou, podél které je místní Lagrangianův smyk maximální (viz obr. 7).
![[t_0, t_1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)




Představujeme dvojrozměrné smykové vektorové pole

a trojrozměrné smykové normální vektorové pole

kritéria pro dvou a trojrozměrné eliptické LCS lze shrnout následovně:
Elipitické podmínky LCS z lokální variační teorie v rozměrech n = 2 a n = 3
| LCS
|
Normální vektorové pole pro n = 3
 |
ODE pro n = 2
 |
PDE typu Frobenius pro n = 3
 |
| Eliptický
|
 |
 ( smykové čáry ) ( smykové čáry ) |
 ( smykové povrchy ) ( smykové povrchy )
|
U 3D toků, jako v případě hyperbolických LCS, se lze vyhnout řešení Frobenius PDE. Místo toho lze sestrojit průsečíky trubicového eliptického LCS s vybranými 2D rovinami a povrch numericky přizpůsobit velkému počtu těchto křivek průsečíků. Pokud jde o výše uvedené hyperbolické LCS, označme normálovou jednotku 2D roviny vztahem . Křižovatkové křivky eliptických LCS s rovinou jsou opět normální pro obě a pro normálovou jednotku LCS. V důsledku toho křivka průsečíku splňuje sníženou smykovou ODE







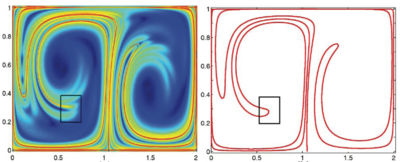
jehož trajektorie označujeme jako redukované smykové čáry . (Přesně řečeno, redukovaná smyková ODE není obyčejná diferenciální rovnice, vzhledem k tomu, že její pravá strana není vektorové pole, ale směrové pole, které obecně není globálně orientovatelné). Průsečíky tubulárních eliptických LCS s jsou mezní cykly ODE se sníženým smykem. Určení takových mezních cyklů v hladké rodině blízkých rovin a potom přizpůsobení povrchu rodině omezených cyklů poskytuje numerickou aproximaci pro 2D smykový povrch. Trojrozměrný příklad tohoto lokálního variačního výpočtu eliptického LCS je znázorněn na obr. 11.



Obrázek 11: Eliptická Lagrangeova koherentní struktura (nebo LCS, zeleně, vlevo) a její advekovaná poloha pod mapou toku (vpravo) chaoticky vynuceného toku ABC. Zeleně je také zobrazen kruh počátečních podmínek umístěný kolem LCS (vlevo), propagovaný po stejnou dobu (vpravo). Obrázek: Daniel Blazevski.
Soudržnost založená na protahování z globálního variačního přístupu: lambda linky
Jak je uvedeno výše u hyperbolických LCS, byl vyvinut globální variační přístup ve dvou dimenzích k zachycení eliptických LCS jako uzavřených stacionárních křivek funkčních průměrů Lagrangianů průměrovaných v materiálové linii. Ukázalo se, že takové křivky jsou uzavřenou nulovou geodetikou generalizované rodiny tenzorů Green – Lagrangeova napětí , kde je kladný parametr (Lagrangeův multiplikátor). Uzavřenou nulovou geodetiku lze ukázat, že se shoduje s mezními cykly rodiny směrových polí



Všimněte si, že pro , směrové pole se shoduje se směrovým polem pro smykové linie získané výše z místní variační teorie LCS.



Trajektorie jsou označovány jako -line. Pozoruhodné jsou počáteční polohy hmotných linií, které se
nekonečně rovnoměrně táhnou pod mapou toku . Konkrétně se jakákoli podmnožina a -line protáhne o faktor mezi časy a . Na obr. 13 je příklad eliptických LCS identifikovaných jako uzavřené linie ve Velké červené skvrně Jupitera.








Parabolické LCS
Parabolické LCS jsou povrchy materiálu bez střihu, které vymezují jádra sad trajektorií tryskového typu. Takové LCS se vyznačují jednak nízkým roztažením (protože jsou uvnitř neroztažné struktury), ale také nízkým střihem (protože střih materiálu je v paprskových jádrech minimální).
Diagnostický přístup: příkopy Lyapunovových exponentů (FTLE) konečného času
Protože jak stříhání, tak roztahování jsou podél parabolického LCS tak nízké, jak je to jen možné, lze hledat počáteční polohy takových povrchů materiálu, jako jsou příkopy pole FTLE . Geofyzikální příklad parabolického LCS (generalizované tryskové jádro) odhalený jako příkop pole FTLE je znázorněn na obr. 14a.

Globální variační přístup: Heteroklinické řetězce nulové geodetiky
Ve dvou dimenzích jsou parabolické LCS také řešení globálního bezstřižného variačního principu popsaného výše pro hyperbolické LCS. Parabolické LCS jako takové se skládají ze smršťovacích čar a úseček, které představují geodetiku Lorentzianova metrického tenzoru . Na rozdíl od hyperbolických LCS však parabolické LCS splňují robustnější okrajové podmínky: zůstávají stacionárními křivkami průměrného smykového průměru materiálové linie i při změnách jejich koncových bodů. To vysvětluje vysoký stupeň robustnosti a pozorovatelnosti, který trysková jádra vykazují při míchání. To je v kontrastu s vysoce citlivou a blednoucí stopou hyperbolických LCS od silně hyperbolických oblastí v difuzních sledovacích vzorcích.

Za hraničních podmínek variabilního koncového bodu se počáteční polohy parabolických LCS ukáží jako střídající se řetězce smršťovacích čar a úseček, které spojují singularity těchto liniových polí. Tyto singularity se vyskytují v bodech, kde , a tudíž nedochází k nekonečně malé deformaci mezi těmito dvěma časovými instancemi a . Obr. 14b ukazuje příklad parabolických LCS v atmosféře Jupitera, umístěných pomocí této variační teorie. Tvary typu chevron, které se tvoří z kruhových bloků materiálu umístěných podél jádra paprsku, jsou charakteristické pro deformaci indikátoru poblíž parabolických LCS.




Obrázek 14b: Parabolické LCS vymezující nestabilní Lagrangeova proudová jádra v atmosféře Jupitera. Rovněž je ukázán vývoj eliptického LCS označujícího hranici Velké červené skvrny. Video: Alireza Hadjighasem.
Softwarové balíčky pro výpočty LCS
Geodetický výpočet 2D hyperbolických a eliptických LCS:
Automatizovaný geodetický výpočet 2D eliptického LCS:
Výpočet 2D a 3D rotačního eliptického LCS:
Advekce částic a konečný čas Lyapunov Výpočet
exponentu :
Viz také
Reference
Další související dokumenty

















![{\ displaystyle {\ mathcal {I}} = [t_ {0}, t_ {1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7c754a3dce189aa23b3fd3df2d2785666384e9c)






![{\ Displaystyle {\ mathcal {M}} = \ {(x, t) \ in {\ mathcal {P}} \ times {\ mathcal {I}} \, \ colon [F_ {t_ {0}}^{ t}]^{-1} (x) \ v {\ mathcal {M}} (t_ {0}) \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0274ca15e373d4c8a1496a3dbf57d1c26f4768bd)










































![{\ Displaystyle C_ {t_ {0}}^{t_ {1}} = \ left [\ nabla F_ {t_ {0}}^{t_ {1}} \ right]^{T} \ nabla F_ {t_ { 0}}^{t_ {1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a4234dd0b40860545b2cc78e272d9ddaf30748)

















![{\ displaystyle [t_ {0}+T, t_ {1}+T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9a619d4eb2db184073ec4bbda335766512d0a10)


![[t_0, t_1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)




























![{\ displaystyle D_ {t_ {0}}^{t_ {1}} (x_ {0}) = {\ frac {1} {2}} \ left [C_ {t_ {0}}^{t_ {1} } (x_ {0}) \ Omega -\ Omega C_ {t_ {0}}^{t_ {1}} (x_ {0}) \ right], \ qquad \ Omega = {\ begin {pmatrix} 0 & -1 \\ 1 a 0 \\\ end {pmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c77b4aed7311063d0230c05d58d13d7a0cf0afdc)




![{\ Displaystyle C_ {t_ {0}}^{t_ {1}} = [\ nabla F_ {t_ {0}}^{t_ {1}}]^{T} \ nabla F_ {t_ {0}}^ {t_ {1}} = U_ {t_ {0}}^{t_ {1}} U_ {t_ {0}}^{t_ {1}} = V_ {t_ {0}}^{t_ {1}} V_ {t_ {0}}^{t_ {1}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5caee8f36db09843a43a2a1236597fd6b2ad9154)





![{\ Displaystyle \ theta _ {t_ {0}}^{t} = \ left [1-{\ rm {sign \,}} \ left (\ sin \ theta _ {t_ {0}}^{t} \ vpravo) \ vpravo] \ pi +{\ rm {znak \,}} \ vlevo (\ sin \ theta _ {t_ {0}} ^{t} \ right) \ cos ^{-1} \ left (\ cos \ theta _ {t_ {0}}^{t} \ right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ab9954ea838550ba7d06fdc58b86bd2690c4fca)



![{\ Displaystyle \ left [K_ {t_ {0}}^{t} \ right] _ {jk} = \ left \ langle \ xi _ {j}, \ nabla F_ {t_ {0}}^{t_ {1 }} \ xi _ {k} \ vpravo \ rangle /{\ sqrt {\ lambda _ {k}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a32d1f98355ad4ac1f6303141bc3b1163833f63)












![{\ Displaystyle {\ dot {\ alpha}} = \ left [W \ left (x (t; x_ {0}), t \ right)-{\ bar {W}} \ left (t \ right) \ right ] \ alpha.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d4ca1677536cdf0c5d9d7f2c462885bf06563a7)




























