Gröbnerův základ - Gröbner basis

V matematice , konkrétněji v počítačové algebře , výpočetní algebraické geometrii a výpočetní komutativní algebře , je Gröbnerův základ konkrétním druhem generující sady ideálu v polynomiálním kruhu K [ x ₁ ,…, x _n ] nad polem K . Gröbnerův základ umožňuje snadno odvodit mnoho důležitých vlastností ideálu a související algebraické odrůdy , jako je rozměr a počet nul, když je konečný. Gröbnerův základový výpočet je jedním z hlavních praktických nástrojů pro řešení systémů polynomiálních rovnic a výpočet obrazů algebraických variet pod projekcemi nebo racionálními mapami .

Gröbnerův výpočet základů lze považovat za vícerozměrnou, nelineární generalizaci jak Euclidova algoritmu pro výpočet největších společných dělitelů polynomu , tak Gaussovu eliminaci pro lineární systémy.

Gröbnerovy báze byly zavedeny v roce 1965, spolu s algoritmem pro jejich výpočet ( Buchbergerův algoritmus ), Bruno Buchberger ve svém Ph.D. teze. Pojmenoval je po svém poradci Wolfgangu Gröbnerovi . V roce 2007 Buchberger obdržel sdružení pro výpočetní techniku ‚s Paris Kanellakis teorie a praxe cenu pro tuto práci. Ruský matematik Nikolaj Günther však zavedl podobný pojem v roce 1913, publikovaný v různých ruských matematických časopisech. Tyto dokumenty byly matematickou komunitou do značné míry ignorovány až do jejich znovuobjevení v roce 1987 Bodo Renschuch et al. Analogický koncept pro vícerozměrné výkonové řady vyvinul nezávisle Heisuke Hironaka v roce 1964, který je pojmenoval standardní základny . Tento termín někteří autoři používali také k označení Gröbnerových základen.

Teorie Gröbnerových základen byla rozšířena mnoha autory v různých směrech. Byl zobecněn na jiné struktury, jako jsou polynomy nad hlavními ideálními kruhy nebo polynomiálními kroužky , a také na některé třídy nekomutativních kruhů a algeber, jako jsou rudy algebry .

Pozadí

Polynomiální prstenec

Gröbner báze jsou primárně definována pro ideály v polynomiální kruhu přes pole K . Ačkoli teorie funguje pro jakékoli pole, většina Gröbnerových základních výpočtů se provádí buď tehdy, když K je pole racionálů, nebo celá čísla modulují prvočíslo. ${\ displaystyle R = K [x_ {1}, \ ldots, x_ {n}]}$

Polynom je součtem , kde jsou nenulové prvky K a jsou monomials nebo „Power produkty“ proměnných. To znamená, že monomiální M je produkt, kde jsou nezáporná celá čísla. Vektor se nazývá exponent vektor z M . Zápis je často zkrácen jako . Monomály jsou jednoznačně definovány svými exponentními vektory, takže počítače mohou efektivně reprezentovat monomie jako exponentní vektory a polynomy jako seznamy exponentních vektorů a jejich koeficientů. ${\ Displaystyle c_ {1} M_ {1} +\ cdots +c_ {m} M_ {m}}$${\ displaystyle c_ {i}}$${\ displaystyle M_ {i}}$${\ Displaystyle M = x_ {1}^{a_ {1}} \ cdots x_ {n}^{a_ {n}},}$${\ displaystyle a_ {i}}$${\ Displaystyle A = [a_ {1}, \ ldots, a_ {n}]}$${\ Displaystyle x_ {1}^{a_ {1}} \ cdots x_ {n}^{a_ {n}} = X^{A}}$

Pokud je konečná množina polynomů v polynomiálním kruhu R , ideál generovaný F je sada lineárních kombinací prvků z F s koeficienty ve všech R : ${\ Displaystyle F = \ {f_ {1}, \ ldots, f_ {k} \}}$

${\ Displaystyle \ langle f_ {1}, \ ldots, f_ {k} \ rangle = \ left \ {\ sum _ {i = 1}^{k} g_ {i} f_ {i} \ mid g_ {1} , \ ldots, g_ {k} \ in K [x_ {1}, \ ldots, x_ {n}] \ right \}.}$

Monomální objednávka

Všechny operace související s Gröbnerovými základnami vyžadují výběr celkového pořadí na monomialích s následujícími vlastnostmi kompatibility s násobením. Pro všechny monomály M , N , P ,

1. ${\ Displaystyle M \ leq N \ Longleftrightarrow MP \ leq NP}$
2. ${\ displaystyle M \ leq MP}$.

Celková objednávka splňující tyto podmínky se někdy nazývá přípustná objednávka .

Tyto podmínky naznačují, že pořadí je dobře uspořádané , to znamená, že každá přísně klesající sekvence monomiálů je konečná.

Ačkoli Gröbnerova teorie základen nezávisí na konkrétní volbě přípustného monomického uspořádání, tři monomické uspořádání jsou zvláště důležité pro aplikace:

• Lexikografické uspořádání , běžně nazývané lex nebo plex (pro čistě lexikální řazení).
• Celkový stupeň reverzního lexikografického uspořádání , běžně nazývaný degrevlex .
• Eliminační objednávka , lexdeg .

Gröbnerova teorie základů byla původně zavedena pro lexikografické uspořádání. Brzy bylo zjištěno, že Gröbnerův základ pro degrevlex je téměř vždy mnohem jednodušší spočítat a že je téměř vždy snazší vypočítat lexův Gröbnerův základ tak, že nejprve vypočítáte základ degrevlexu a poté použijete „změnu algoritmu řazení“. Když je potřeba eliminace , degrevlex není vhodný; lze použít lex i lexdeg, ale opět je mnoho výpočtů s lexdeg relativně snadné a s lex téměř nemožné.

Jakmile je stanoveno monomické uspořádání, termíny polynomu (součin monomia s nenulovým koeficientem) jsou přirozeně seřazeny podle klesajících monomií (pro toto pořadí). Díky tomu je reprezentace polynomu jako uspořádaný seznam dvojic vektorů koeficient – ​​exponent kanonickou reprezentací polynomů. První (největší) člen polynomu p pro toto uspořádání a odpovídající monomický a koeficient se příslušně nazývají úvodní termín , vedoucí monomický a úvodní koeficient a v tomto článku označují lt ( p ), lm ( p ) a lc ( p ).

Snížení

Pro Gröbnerovu teorii základů je koncept redukce , nazývaný také vícerozměrné dělení nebo výpočet normální formy . Jedná se o vícerozměrné zobecnění euklidovského dělení univariačních polynomů .

V této části předpokládáme pevné monomické řazení, které nebude definováno explicitně.

Vzhledem ke dvěma polynomům f a g jeden říká, že f je redukovatelné o g, pokud nějaké monomiální m ve f je násobkem úvodního monomického lm ( g ) z g . Pokud je m náhodou vedoucí monomiál f, pak se říká, že f je olově redukovatelné o g . Pokud c je koeficient m ve f a m = Q lm ( g ), přičemž snížení jednostupňový z f o g je operace, která se stýká se f polynomu

${\ displaystyle \ operatorname {red} _ {1} (f, g) = f-{\ frac {c} {\ operatorname {lc} (g)}} \, q \, g.}$

Hlavními vlastnostmi této operace je, že výsledný polynom neobsahuje monomiální m a že monomie větší než m (pro monomiální uspořádání) zůstávají nezměněny. Tato operace není obecně jednoznačně definována; je -li několik monomiálů ve f násobky lm ( g ), pak si člověk může libovolně zvolit, který z nich sníží. V praxi je lepší vybrat největší pro monomické uspořádání, protože jinak by následné redukce mohly znovu zavést právě odstraněný monomial.

Vzhledem k tomu, konečný soubor G polynomů, jeden říká, že f je redukovat nebo olovo-redukovatelné od G , je-li redukovat nebo olovo-redukovatelné, v daném pořadí, od elementu g G . Pokud je tomu tak, pak jeden definuje . The (kompletní) redukce f od G spočívá v tom, iterativně tento operátor do získání polynom , který je nesnížitelný od G . To se nazývá normální forma o f u G . Obecně tato forma není jednoznačně definována (nejedná se o kanonickou formu ); tato jedinečnost je výchozím bodem Gröbnerovy teorie základů. ${\ displaystyle \ operatorname {red} _ {1} (f, G) = \ operatorname {red} _ {1} (f, g)}$${\ displaystyle \ operatorname {red} _ {1}}$${\ displaystyle \ operatorname {red} (f, G)}$

U Gröbnerových výpočtů, s výjimkou na konci, není nutné provádět úplnou redukci: postačuje redukce olova , která ušetří velké množství výpočtů.

Definice redukce okamžitě ukazuje, že pokud h je normální forma f podle G , pak máme

${\ Displaystyle f = h+\ sum _ {g \ v G} q_ {g} \, g,}$

kde jsou polynomy. V případě univariačních polynomů, pokud G sestává z jediného prvku g , pak h je zbytek euklidovského dělení f na g , q _g je kvocient a dělící algoritmus je přesně proces redukce olova. Z tohoto důvodu někteří autoři používají místo redukce termín vícerozměrné dělení . ${\ displaystyle q_ {g}}$

Příklady redukce

V příkladech této části mají polynomy tři neurčité x , y a z a použité monomické pořadí je monomické, přičemž pro srovnání dvou monomiálů jeden nejprve porovnává exponenty x ; pouze když jsou exponenciály x stejné, porovnává se exponent y ; a exponenty z jsou porovnávány pouze tehdy, když jsou ostatní exponenty stejné. ${\ Displaystyle x \ succ y \ succ z;}$

Abychom měli jasný přehled o procesu redukce, musíme přepsat polynomy s jejich členy v sestupném pořadí. Například pokud

${\ Displaystyle P = xy^{3} z^{5}+x^{2} y^{6}+x^{4} yz+y^{2} z^{5}+yz^{4} +y^{3}+z^{3}+xy+xz+z^{2}+z,}$

musí se to přepsat

${\ Displaystyle P = x^{4} yz+x^{2} y^{6}+xy^{3} z^{5}+xy+xz+y^{3}+y^{2} z ^{5}+yz^{4}+z^{3}+z^{2}+z.}$

To umožňuje mít první monomiální jako první (pro zvolené pořadí); tady${\ displaystyle \ operatorname {lm} (P) = x^{4} yz.}$

Zvážit snížení o s a${\ Displaystyle f = 2x^{3} -x^{2} y+y^{3}+3y \;}$${\ Displaystyle \; G = \ {g_ {1}, g_ {2} \},}$${\ Displaystyle g_ {1} = x^{2}+y^{2} -1}$${\ displaystyle g_ {2} = xy-2.}$

Pro první redukční krok může být redukován buď první z druhého členu. Snížení termínu však znamená odstranění tohoto výrazu za cenu přidání nových nižších termínů, a pokud to není první redukovatelný termín, který je redukován, je možné, že další redukce přidá podobný termín, který musí být opět snížen. Je proto vždy lepší nejprve redukovat největší (pro monomické pořadí) redukovatelné členy.

Přední termín z f je redukovatelný Takže první redukční stupeň sestává z násobení od -2 x a přidáním výsledek f : ${\ displaystyle 2x^{3}}$${\ displaystyle g_ {1}.}$${\ displaystyle g_ {1}}$

${\ Displaystyle f \; {\ overset {-2xg_ {1}} {\ longrightarrow}} \; f_ {1} = f-2xg_ {1} =-x^{2} y-2xy^{2}+2x +y^{3}+3 roky.}$

Jako vedoucí termín z je násobkem předních monomials obou a jeden má dvě možnosti pro druhý redukční stupeň. Pokud si někdo vybere, získá polynom, který lze znovu zmenšit o${\ displaystyle -x^{2} y}$${\ displaystyle f_ {1}}$${\ displaystyle g_ {1}}$${\ displaystyle g_ {2},}$${\ displaystyle g_ {2},}$${\ displaystyle g_ {2} \ colon}$

${\ Displaystyle f \; {\ overset {-2xg_ {1}} {\ longrightarrow}} \; f_ {1} \; {\ overset {xg_ {2}} {\ longrightarrow}} \;-2xy^{2 }+y^{3}+3y \; {\ overset {2yg_ {2}} {\ longrightarrow}} \; f_ {2} =+y^{3} -y.}$

Další redukce není možná, lze ji tedy zvolit pro úplné snížení f . Jeden však získá jiný výsledek s druhou volbou pro druhý krok: ${\ displaystyle f_ {2}}$

${\ Displaystyle f \; {\ overset {-2xg_ {1}} {\ longrightarrow}} \; f_ {1} \; {\ overset {yg_ {1}} {\ longrightarrow}} \;-2xy^{2 }+2x+2y^{3}+2y \; {\ overset {2yg_ {2}} {\ longrightarrow}} \; f_ {3} =+2x+2y^{3} -2y.}$

Úplné snížení f tedy může mít za následek buď nebo${\ displaystyle f_ {2}}$${\ displaystyle f_ {3}.}$

Byl zaveden Buchbergerův algoritmus pro řešení obtíží způsobených touto jedinečností. Zjednodušeně řečeno spočívá přidat do G polynomy, které jsou potřebné k jedinečnosti redukce G .

Zde by Buchbergerův algoritmus začal přidáním polynomu do G

${\ displaystyle g_ {3} = yg_ {1} -xg_ {2} = 2x+y^{3} -y.}$

Skutečně lze dále snížit o a toto opět produkuje . Tím se však Buchbergerův algoritmus nedokončí, protože xy dává různé výsledky, když se sníží o nebo${\ displaystyle f_ {3}}$${\ displaystyle g_ {3},}$${\ displaystyle f_ {2}}$${\ displaystyle g_ {2}}$${\ displaystyle g_ {3}.}$

Formální definice

Gröbner základ G ideálu I v polynomu kruhu R přes pole je generování sada z I vyznačující se tím, jednoho z následujících vlastností, uvedené relativně k nějaké monomial pořadí :

• ideál generovaný úvodními termíny polynomů v I se rovná ideálu generovanému úvodními termíny G ;
• úvodní člen jakéhokoli polynomu v I je dělitelný vedoucím členem nějakého polynomu v G ;
• vícerozměrná rozdělení jakéhokoli polynom polynomu kruhu R u G dává jedinečnou zbytek;
• multivariační dělení G libovolného polynomu v ideálu I dává zbytek 0 .

Všechny tyto vlastnosti jsou ekvivalentní; různí autoři používají různé definice v závislosti na zvoleném tématu. Poslední dvě vlastnosti umožňují výpočty v faktorovém prstenci R/I se stejným zařízením jako modulární aritmetika. Je významnou skutečností komutativní algebry, že Gröbnerovy báze vždy existují a lze je efektivně vypočítat pro jakýkoli ideál daný konečnou generující podmnožinou.

Dělení s více proměnnými vyžaduje monomiální řazení, základ závisí na zvoleném monomickém uspořádání a z různých uspořádání může vzniknout radikálně odlišný Gröbnerův základ. Dva z nejčastěji používaných uspořádání jsou lexikografické uspořádání a stupeň reverzní lexikografické pořadí (také nazývané odstupňované reverzní lexikografické pořadí nebo jednoduše celkový stupeň pořadí ). Lexikografická objednávka eliminuje proměnné, nicméně výsledné Gröbnerovy báze jsou často velmi velké a jejich výpočet je drahý. Stupně reverzní lexikografické pořadí obvykle poskytuje nejrychlejší Gröbnerovy výpočty. V tomto pořadí jsou monomy porovnávány nejprve podle celkového stupně, přičemž vazby jsou přerušeny tím, že se vezme nejmenší monomiál s ohledem na lexikografické uspořádání s obrácenými proměnnými.

Ve většině případů (polynomy v konečném počtu proměnných s komplexními koeficienty nebo obecněji například s koeficienty pro jakékoli pole) existují Gröbnerovy báze pro jakékoli monomiální uspořádání. Buchbergerův algoritmus je nejstarší a nejznámější metodou pro jejich výpočet. Dalšími metodami jsou Faugèrovy algoritmy F4 a F5 , založené na stejné matematice jako Buchbergerův algoritmus, a evolventivní přístupy založené na myšlenkách z diferenciální algebry . Tam jsou také tři algoritmy pro převod základ Gröbner ve vztahu k jednomu monomial aby základ Gröbner vzhledem k odlišnému monomial pořadí: FGLM algoritmus je Hilbert řízený algoritmus a algoritmus Gröbner chůze . Tyto algoritmy se často používají k výpočtu (obtížných) lexikografických Gröbnerových základen z (snadnějších) celkových stupňů Gröbnerových základen.

Gröbnerův základ se nazývá snížený, pokud je počáteční koeficient každého prvku základu 1 a žádný monomický v žádném prvku základu není v ideálu generovaném úvodními členy ostatních prvků základu. V nejhorším případě může výpočet Gröbnerova základu vyžadovat čas, který je exponenciální nebo dokonce dvojnásobně exponenciální v počtu řešení polynomiálního systému (pro stupeň reverzního lexikografického pořadí a lexikografického pořadí). Navzdory těmto hranicím složitosti jsou standardní i redukované Gröbnerovy báze v praxi často vyčíslitelné a většina systémů počítačové algebry obsahuje rutiny, jak toho dosáhnout.

Koncepce a algoritmy Gröbnerovy základen byly zobecněny do submodulů z volné moduly přes polynomial prsten. Ve skutečnosti, je -li L volným modulem nad prstencem R , pak lze uvažovat R ⊕ L jako prstenec definováním součinu dvou prvků L jako 0. Tento kruh lze ztotožnit s , kde je základ L . To umožňuje identifikovat submodul L vytvořeného s ideálu generované a produkty , . Je -li R polynomiální prsten, redukuje to teorii a algoritmy Gröbnerových základen modulů na teorii a algoritmy Gröbnerových základen ideálů. ${\ Displaystyle R [e_ {1}, \ ldots, e_ {l}]/\ left \ langle \ {e_ {i} e_ {j} | 1 \ leq i \ leq j \ leq l \} \ right \ rangle }$${\ displaystyle e_ {1}, \ ldots, e_ {l}}$${\ displaystyle g_ {1}, \ ldots, g_ {k}}$${\ displaystyle R [e_ {1}, \ ldots, e_ {l}]}$${\ displaystyle g_ {1}, \ ldots, g_ {k}}$${\ displaystyle e_ {i} e_ {j}}$${\ Displaystyle 1 \ leq i \ leq j \ leq l}$

Koncept a algoritmy Gröbnerových bází byly také zobecněny na ideály na různých prstencích, komutativních nebo ne, jako polynomické prstence na hlavním ideálním kruhu nebo Weylových algebrách .

Příklad a protipříklad

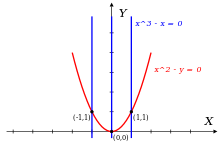
Nechme být prstenem bivariátových polynomů s racionálními koeficienty a uvažujme ideál generovaný polynomy ${\ Displaystyle R = \ mathbb {Q} [x, y]}$${\ Displaystyle I = \ langle f, g \ rangle}$

${\ Displaystyle f (x, y) = x^{2} -y}$,

${\ Displaystyle g (x, y) = x^{3} -x}$.

Dva další prvky I jsou polynomy

k ( x , y ) = - xf ( x , y ) + g ( x , y ) = xy - x

h ( x , y ) = xk ( x , y ) - ( y - 1) f ( x , y ) = y ² - y

Pod lexikografickým uspořádáním s máme ${\ displaystyle x> y}$

lt ( f ) = x ²

lt ( g ) = x ³

lt ( h ) = y ²

Ideál generovaný pomocí {lt ( f ), lt ( g )} obsahuje pouze polynomy, které jsou dělitelné x ^2, což vylučuje lt ( h ) = y ² ; z toho vyplývá, že { f , g } není Gröbnerovým základem pro I.

Na druhé straně můžeme ukázat, že { f , k , h } je skutečně Gröbnerovým základem pro I.

Za prvé, f a g, a tedy také h, k a všechny ostatní polynomy v ideálu, mám společné následující tři nuly v rovině ( x , y ), jak je znázorněno na obrázku: {(1,1), (−1,1), (0,0)}. Tyto tři body nejsou kolineární, takže jsem neobsahuje žádný polynom prvního stupně. Také nemohu obsahovat žádné polynomy speciální formy

m ( x , y ) = cx + p ( y )

s c nenulovým racionálním číslem a p polynomem pouze v proměnné y ; důvodem je, že takové m nikdy nemůže mít dvě odlišné nuly se stejnou hodnotou pro y (v tomto případě body (1,1) a (−1,1)).

Z výše uvedeného vyplývá, že já, kromě nulového polynomu, obsahuje pouze polynomy, jejichž počáteční člen má stupeň větší nebo rovný 2; proto jsou jejich úvodní členy dělitelné alespoň jedním ze tří monomiálů

{ x ² , xy , y ² } = {lt ( f ), lt ( k ), lt ( h )}.

To znamená, že { f , k , h } je Gröbnerův základ pro I s ohledem na lexikografické uspořádání s x > y.

Vlastnosti a aplikace základů Gröbner

Pokud není výslovně uvedeno, všechny následující výsledky platí pro jakékoli monomické řazení (definice různých řádů, které jsou uvedeny níže), najdete v tomto článku).

Je běžnou mylnou představou, že pro některé z těchto výsledků je zapotřebí lexikografické uspořádání. Naopak, lexikografické pořadí je téměř vždy nejobtížněji vypočítatelné a jeho použití činí nepraktické mnoho výpočtů, které jsou relativně snadné s odstupňovaným reverzním lexikografickým uspořádáním (grevlex), nebo je -li potřeba eliminace, s eliminačním pořadím (lexdeg ), která omezuje na grevlex na každém bloku proměnných.

Rovnost ideálů

Redukované základny Gröbner jsou jedinečné pro jakýkoli daný ideál a jakékoli monomické uspořádání. Dva ideály jsou si tedy rovny právě tehdy, pokud mají stejný (redukovaný) Gröbnerův základ (obvykle software Gröbnerova základu vždy vytváří redukované Gröbnerovy základy).

Členství a zahrnutí ideálů

Snížení polynomu f podle Gröbner základě G ideálu I vzdá 0 tehdy a jen tehdy, pokud f je v I . To umožňuje otestovat členství prvku v ideálu. Další metoda spočívá v ověření, zda Gröbner základem G ∪ { f } je roven G .

Pro test, zda je ideální I generované f ₁ , ...,  f _K obsažené v ideální J , stačí test, který každý f _i je v J . Lze také vyzkoušet rovnost redukovaných Gröbnerových základen J a J  ∪ { f ₁ , ..., f _k }.

Řešení soustavy algebraických rovnic

Na libovolnou sadu polynomů lze pohlížet jako na systém polynomiálních rovnic tím, že polynomy se rovnají nule. Sada řešení takového systému závisí pouze na generovaném ideálu, a proto se nemění, když je daná generující sada nahrazena Gröbnerovým základem pro jakékoli uspořádání generovaného ideálu. Takové řešení se souřadnicemi v algebraicky uzavřeném poli obsahujícím koeficienty polynomů se nazývá nula ideálu . V obvyklém případě racionálních koeficientů je toto algebraicky uzavřené pole vybráno jako komplexní pole .

Ideál nemá žádnou nulu (soustava rovnic je nekonzistentní ) právě tehdy, pokud 1 patří ideálu (toto je Hilbertův Nullstellensatz ), nebo ekvivalentně, pokud jeho Gröbnerův základ (pro jakékoli monomické uspořádání) obsahuje 1, nebo, také v případě, že odpovídající redukovaný Gröbnerův základ je [1].

Vzhledem k Gröbner základem G ideálu I , má jen omezený počet nul, tehdy a jen tehdy, pokud pro každou proměnnou x , G obsahuje polynom s předním monomial, který je síla x (bez jakékoli další proměnná objevuje ve vedoucí termín). Je-li tomu tak, pak je počet nul, počítá s mnohosti, je roven počtu monomials, které nejsou násobky jakéhokoliv vedoucího monomial z G . Toto číslo se nazývá mírou ideálu.

Když je počet nul konečný, poskytuje Gröbnerův základ pro lexikografické monomické uspořádání teoreticky řešení: první souřadnice řešení jsou kořenem největšího společného dělitele polynomů základu, který závisí pouze na první proměnné. Po nahrazení tohoto kořene v základu jsou druhé souřadnice tohoto řešení kořenem největšího společného dělitele výsledných polynomů, který závisí pouze na této druhé proměnné atd. Tento proces řešení je pouze teoretický, protože zahrnuje výpočet GCD a hledání kořenů polynomů s přibližnými koeficienty, které nejsou proveditelné z důvodu numerické nestability. Proto byly vyvinuty další metody k řešení polynomiálních systémů pomocí Gröbnerových základen ( další podrobnosti viz Systém polynomiálních rovnic ).

Dimenze, stupeň a Hilbertova řada

Rozměr ideálního I v polynomu kruhu R je rozměr KRULL prstencového R / I a je rovna rozměru algebraické množiny nul I . Rovněž se rovná počtu nadrovin v obecné poloze, které jsou potřebné k průniku s algebraickou sadou, což je konečný počet bodů. Stupeň ideálu a jeho přidružené algebraické sady je počet bodů této konečné křižovatky, počítá s opakování. Zejména je stupeň hyperpovrchu roven stupni jeho definičního polynomu.

Stupeň i rozměr závisí pouze na sadě předních monomiálů na Gröbnerově základě ideálu pro jakékoli monomiální uspořádání.

Rozměr je velikost maximální podmnožiny S proměnných tak, že není vedoucí monomial v závislosti pouze na proměnných S . Pokud má tedy ideál rozměr 0, pak pro každou proměnnou x existuje v Gröbnerově základu vedoucí monomie, která je mocninou x .

Dimenze i stupeň lze odvodit z Hilbertovy řady ideálu, což je řada , kde je počet monomiálů stupně i, které nejsou násobkem žádného vedoucího monomialu na Gröbnerově základě. Hilbertovu sérii lze shrnout do racionálního zlomku ${\ textstyle \ sum _ {i = 0}^{\ infty} d_ {i} t^{i}}$${\ displaystyle d_ {i}}$

${\ Displaystyle \ sum _ {i = 0}^{\ infty} d_ {i} t^{i} = {\ frac {P (t)} {(1-t)^{d}}},}$

kde d je rozměr ideálu a je polynom takový, jaký je stupeň ideálu. ${\ displaystyle P (t)}$${\ displaystyle P (1)}$

Ačkoli dimenze a stupeň nezávisí na volbě monomického uspořádání, Hilbertova řada a polynom se mění, když se změní monomiální uspořádání. ${\ displaystyle P (t)}$

Většina počítačových algebraických systémů, které poskytují funkce pro výpočet Gröbnerových základen, poskytuje také funkce pro výpočet Hilbertovy řady, a tedy také rozměr a stupeň.

Odstranění

Výpočet Gröbnerových základen pro eliminační monomické uspořádání umožňuje výpočetní eliminační teorii . To je založeno na následující větě.

Uvažujme polynomiální kruh , ve kterém jsou proměnné rozděleny do dvou podskupin X a Y . Vyberme také eliminační monomiální uspořádání „eliminující“ X , to je monomické uspořádání, pro které jsou porovnávány dva monomeny, nejprve porovnáním X -dílů a v případě rovnosti pouze s Y -díly. To znamená, že monomial obsahující X -variable je větší než každý monomial nezávisle na X . Pokud G je Gröbnerovým základem ideálu I pro toto monomické uspořádání, pak je Gröbnerovým základem (tento ideál se často nazývá eliminační ideál ). Navíc se skládá přesně z polynomů G, jejichž úvodní členy patří do K [ Y ] (to velmi usnadňuje výpočet , protože je třeba zkontrolovat pouze úvodní monomialy). ${\ Displaystyle K [x_ {1}, \ ldots, x_ {n}, y_ {1}, \ ldots, y_ {m}] = K [X, Y],}$${\ Displaystyle G \ cap K [Y]}$${\ Displaystyle I \ cap K [Y]}$${\ Displaystyle G \ cap K [Y]}$${\ Displaystyle G \ cap K [Y]}$

Tato vlastnost eliminace má mnoho aplikací, některé z nich jsou uvedeny v následujících částech.

Další aplikace, v algebraické geometrii , je, že eliminace realizuje geometrické provoz projekce z k afinní algebraické sady do podprostoru okolního prostoru: s výše notace je ( Zariski uzávěr z) průmět algebraické množiny definovány ideální I do Y -podprostoru je definován ideálem${\ Displaystyle I \ cap K [Y].}$

Lexikografické uspořádání takové, že je eliminačním uspořádáním pro každý oddíl. Gröbnerův základ pro toto řazení tedy nese mnohem více informací, než je obvykle nutné. To může vysvětlovat, proč jsou Gröbnerovy základy pro lexikografické uspořádání obvykle nejobtížněji vypočítatelné. ${\ displaystyle x_ {1}> \ cdots> x_ {n}}$${\ Displaystyle \ {x_ {1}, \ ldots, x_ {k} \}, \ {x_ {k+1}, \ ldots, x_ {n} \}.}$

Protínající se ideály

Pokud I a J jsou dva ideály generované příslušně pomocí { f ₁ , ..., f _m } a { g ₁ , ..., g _k }, pak jeden Gröbnerův výpočet základu vytvoří Gröbnerův základ jejich průniku I  ∩  J . Za tímto účelem jeden zavádí nový neurčitý t a jeden používá eliminační uspořádání tak, že první blok obsahuje pouze t a druhý blok obsahuje všechny ostatní proměnné (to znamená, že monomiál obsahující t je větší než každý monomiál, který neobsahuje t ). S tímto monomickým uspořádáním se Gröbnerův základ I  ∩  J skládá z polynomů, které neobsahují t , v Gröbnerově základu ideálu

${\ Displaystyle K = \ langle tf_ {1}, \ ldots, tf_ {m}, (1-t) g_ {1}, \ ldots, (1-t) g_ {k} \ rangle.}$

Jinými slovy, I  ∩  J se získá odstraněním t v K . To lze dokázat poznámkou, že ideální K spočívá v polynomech takových, že a . Takový polynom je nezávislý na t if a pouze a = b , což znamená, že${\ displaystyle (ab) t+b}$${\ displaystyle a \ in I}$${\ displaystyle b \ v J}$${\ Displaystyle b \ in I \ cap J.}$

Implicitizace racionální křivky

Racionální křivka je algebraická křivka , která má parametrické rovnice ve tvaru

${\ Displaystyle {\ begin {aligned} x_ {1} & = {\ frac {f_ {1} (t)} {g_ {1} (t)}} \ \ & \; \; \ vdots \\ x_ { n} & = {\ frac {f_ {n} (t)} {g_ {n} (t)}}, \ end {aligned}}}$

kde a jsou univariační polynomy pro 1 ≤ i ≤ n . Jeden může (a bude) předpokládat, že a jsou coprime (nemají žádné nekonstantní společné faktory). ${\ displaystyle f_ {i} (t)}$${\ displaystyle g_ {i} (t)}$${\ displaystyle f_ {i} (t)}$${\ displaystyle g_ {i} (t)}$

Implicitizace spočívá ve výpočtu implicitních rovnic takové křivky. V případě n = 2, tj. Pro rovinné křivky, to lze vypočítat s výslednicí . Implicitní rovnice je následující výsledek:

${\ displaystyle {\ text {Res}} _ {t} (g_ {1} x_ {1} -f_ {1}, g_ {2} x_ {2} -f_ {2}).}$

Eliminace pomocí Gröbnerových základen umožňuje implicitizovat jakoukoli hodnotu n , jednoduše odstraněním t v ideálním případě Pokud n = 2, výsledek je stejný jako u výslednice, pokud je mapa injektivní téměř pro každé t . V druhém případě je výslednice mocninou výsledku eliminace. ${\ Displaystyle \ langle g_ {1} x_ {1} -f_ {1}, \ ldots, g_ {n} x_ {n} -f_ {n} \ rangle.}$${\ displaystyle t \ mapsto (x_ {1}, x_ {2})}$

Nasycení

Při modelování problému pomocí polynomiálních rovnic je velmi časté, že některé veličiny mají být nenulové, protože pokud jsou nulové, problém se velmi liší. Například při jednání s trojúhelníky se mnoho vlastností stane falešnými, pokud je trojúhelník degenerován, to znamená, že pokud je délka jedné strany rovna součtu délek ostatních stran. V takových situacích není naděje na odvození příslušných informací z polynomiálního systému, pokud nevypadnou degenerovaná řešení. Přesněji řečeno, systém rovnic definuje algebraickou množinu, která může mít několik neredukovatelných složek , a je třeba odstranit složky, na nichž jsou podmínky degenerace všude nulové.

To se provádí nasycením rovnic podmínkami degenerace, což lze provést pomocí vlastnosti eliminace Gröbnerových bází.

Definice sytosti

Lokalizace prstence spočívá v tom, přiléhající k ní formální inverze některých prvků. Tato část se týká pouze případu jednoho prvku nebo ekvivalentně konečného počtu prvků (sousedící s inverzemi několika prvků je ekvivalentní s inverzí jejich součinu). Lokalizace z prstence R prvkem f je kruh , kde t je nový neurčitý představuje inverzní f . Lokalizace ideálního I o R je ideální z Když R je polynom kruh, výpočetní v není efektivní, protože je třeba řídit jmenovatele. Proto je operace lokalizace obvykle nahrazena operací nasycení . ${\ displaystyle R_ {f} = R [t]/(1-ft),}$${\ displaystyle R_ {f} I}$${\ displaystyle R_ {f}.}$${\ displaystyle R_ {f}}$

The nasycení vzhledem kfideáluIvRje inverzní obrazza kanonické mapy zRnato ideálníspočívající v všechny prvkyR, jejichž produkty nějakou siloufpatříI. ${\ displaystyle R_ {f} I}$${\ displaystyle R_ {f}.}$${\ Displaystyle I: f^{\ infty} = \ {g \ in R | (\ existuje k \ in \ mathbb {N}) f^{k} g \ in I \}}$

Pokud J je ideál generovaný I a 1 ft v R [ t ], pak z toho vyplývá, že pokud R je polynomický prstenec, Gröbnerův výpočet eliminující t umožňuje vypočítat Gröbnerův základ nasycení ideálu pomocí polynom. ${\ Displaystyle I: f^{\ infty} = J \ cap R.}$

Důležitou vlastností nasycení, což zajišťuje, že se odstraní z algebraické množiny definované ideální I se nesnížitelné součásti , na kterých polynom f je nula, je následující: primární rozklad z spočívá ve složek primárního rozkladu I které neobsahují žádnou mocninu f . ${\ Displaystyle I: f^{\ infty}}$

Výpočet nasycení

Gröbnerův základ nasycení f polynomiálního ideálu generovaného konečnou sadou polynomů F lze získat vyloučením t v tom smyslu, že polynomy zůstanou nezávislé na t v Gröbnerově základě pro eliminační uspořádání eliminující t . ${\ Displaystyle F \ cup \ {1-tf \},}$${\ Displaystyle F \ cup \ {1-tf \}}$

Namísto použití F , jeden může také vycházet z Gröbner základě F . Která metoda je nejúčinnější, závisí na problému. Pokud však saturace neodstraní žádnou složku, tj. Pokud se ideál rovná jejímu nasycenému ideálu, vypočítá se nejprve Gröbnerův základ F obvykle rychleji. Na druhou stranu, pokud saturace odstraní některé komponenty, přímý výpočet může být dramaticky rychlejší.

Pokud chce někdo nasytit s ohledem na několik polynomů nebo s ohledem na jeden polynom, který je součinem, existují tři způsoby, jak postupovat stejně, ale mohou mít velmi odlišné časy výpočtu (záleží na problému, který je nejefektivnější ). ${\ displaystyle f_ {1}, \ ldots, f_ {k}}$${\ Displaystyle f = f_ {1} \ cdots f_ {k},}$

• Nasycení jediným Gröbnerovým základním výpočtem.${\ Displaystyle f = f_ {1} \ cdots f_ {k}}$
• Nasycení poté nasycením výsledku a tak dále.${\ displaystyle f_ {1},}$${\ displaystyle f_ {2},}$
• Sečtením F nebo jeho Gröbnerovým základem polynomy a odstraněním jediného Gröbnerova základního výpočtu.${\ Displaystyle 1-t_ {1} f_ {1}, \ ldots, 1-t_ {k} f_ {k},}$${\ displaystyle t_ {i}}$

Efektivní Nullstellensatz

Hilbert's Nullstellensatz má dvě verze. První z nich tvrdí, že sada polynomů má prázdnou sadu společných nul v algebraickém uzavření pole koeficientů právě tehdy, pokud 1 patří generovanému ideálu. To lze snadno otestovat pomocí Gröbnerova výpočtu, protože 1 patří ideálu právě tehdy, pokud 1 patří Gröbnerovu základu ideálu, pro jakékoli monomiální řazení.

Druhá verze tvrdí, že množina společných nul (v algebraickém uzavření pole koeficientů) ideálu je obsažena v nadpovrchovém povrchu nul polynomu f , právě tehdy, pokud k ideálu náleží mocnina f . To lze testovat saturací ideálu o f ; ve skutečnosti mocnina f patří k ideálu právě tehdy, když nasycení f poskytuje Gröbnerův základ obsahující 1.

Implicitizace ve vyšší dimenzi

Podle definice lze afinní racionální rozmanitost dimenze k popsat parametrickými rovnicemi formy

${\ displaystyle {\ begin {aligned} x_ {1} & = {\ frac {p_ {1}} {p_ {0}}} \\ & \; \; \ vdots \\ x_ {n} & = {\ frac {p_ {n}} {p_ {0}}}, \ end {aligned}}}$

kde je n +1 polynomů v k proměnných (parametry parametrizace) Parametry a souřadnice bodů odrůdy jsou tedy nuly ideálu ${\ displaystyle p_ {0}, \ ldots, p_ {n}}$${\ Displaystyle t_ {1}, \ ldots, t_ {k}.}$${\ displaystyle t_ {1}, \ ldots, t_ {k}}$${\ displaystyle x_ {1}, \ ldots, x_ {n}}$

${\ Displaystyle I = \ left \ langle p_ {0} x_ {1} -p_ {1}, \ ldots, p_ {0} x_ {n} -p_ {n} \ right \ rangle.}$

Dalo by se hádat, že k odstranění implicitních rovnic odrůdy stačí eliminovat parametry, jak se to dělo v případě křivek. Bohužel tomu tak není vždy. V případě, že mají společný nulový (někdy se nazývá referenční bod ), každý neredukovatelnou složku algebraická sady neprázdná je definován je ireducibilní složkou algebraické množiny definované I . Z toho vyplývá, že v tomto případě přímá eliminace poskytuje prázdnou sadu polynomů. ${\ displaystyle p_ {i}}$${\ displaystyle p_ {i}}$${\ displaystyle t_ {i}}$

Pokud tedy k > 1 jsou k implicitizaci zapotřebí dva Gröbnerovy výpočty:

1. Nasyťte , abyste získali Gröbnerův základ${\ displaystyle I}$${\ displaystyle p_ {0}}$${\ displaystyle G}$
2. Odstraněním od získáte Gröbnerův základ ideálu (implicitních rovnic) odrůdy.${\ displaystyle t_ {i}}$${\ displaystyle G}$

Implementace

• Bezplatný počítačový algebraický systém CoCoA pro výpočet Gröbnerových základen.
• Bezplatný počítačový algebraický systém GAP, který dokáže provádět výpočty Gröbnerových základen.
• FGb, Faugèrova vlastní implementace jeho algoritmu F4 , dostupná jako knihovna Maple . K dnešnímu dni je to s Magmou nejrychlejší implementace racionálních koeficientů a koeficientů v konečném poli primárního řádu.
• Macaulay 2 bezplatný software pro provádění polynomických výpočtů, zejména výpočtů Gröbnerových základen.
• Magma má velmi rychlou implementaci Faugèrova algoritmu F4.
• Maple má implementace algoritmů Buchberger a Faugère F4 a také Gröbnerovu stopu.
• Mathematica zahrnuje implementaci Buchbergerova algoritmu s technikami zlepšujícími výkon, jako je Gröbnerova procházka, Gröbnerova stopa a vylepšení torických základen.
• SINGULÁRNÍ svobodný software pro výpočet komutativních a nekomutativních Gröbnerových základen.
• SageMath poskytuje jednotné rozhraní pro několik systémů počítačové algebry (včetně SINGULAR a Macaulay) a obsahuje několik vlastních algoritmů založených na Gröbneru .
• Počítačový algebraický systém SymPy Python využívá k řešení polynomiálních systémů Gröbnerovy báze.

Oblasti použití

Kódy pro opravu chyb

Gröbnerův základ byl použit v teorii kódů opravujících chyby pro algebraické dekódování. Použitím Gröbnerova základního výpočtu na různých formách rovnic opravujících chyby byly vyvinuty dekódovací metody pro opravu chyb cyklických kódů, afinitních varietních kódů, algebraicko-geometrických kódů a dokonce i obecných lineárních blokových kódů. Aplikace Gröbnerova základu v algebraickém dekódování je stále oblastí výzkumu teorie kódování kanálů.

Viz také

Reference

Další čtení

• Adams, William W .; Loustaunau, Philippe (1994). Úvod do Gröbnerových základen . Postgraduální studium matematiky . 3 . Americká matematická společnost . ISBN 0-8218-3804-0.
• Li, Huishi (2011). Gröbnerovy základy v prstencové teorii . World Scientific . ISBN 978-981-4365-13-0.
• Becker, Thomas; Weispfenning, Volker (1998). Gröbnerovy základny . Absolventské texty z matematiky. 141 . Springer. ISBN 0-387-97971-9.
• Buchberger, Bruno (1965). Algoritmus pro hledání základních prvků prstenu třídy reziduí ideálu polynomu s nulovou dimenzí (PDF) (PhD). Univerzita v Innsbrucku. - (2006). Přeložil Abramson, M. „Doktorská práce Bruna Buchbergera 1965: Algoritmus pro nalezení základních prvků prstence třídy zbytků polynomiálního ideálu nulové dimenze“ . Journal of Symbolic Computation . 41 (3–4): 471–511. doi : 10.1016/j.jsc.2005.09.007 . [Toto je Buchbergerova práce vynalézající Gröbnerovy základny.]
• Buchberger, Bruno (1970). „Algoritmické kritérium řešitelnosti soustavy algebraických rovnic“ (PDF) . Aequationes Mathematicae . 4 : 374–383. doi : 10,1007/BF01844169 . S2CID  189834323 . (Toto je časopisecká publikace Buchbergerovy práce.) Burchberger, B .; Winkler, F., eds. (26. února 1998). „Algoritmické kritérium řešitelnosti soustavy algebraických rovnic“ . Gröbnerovy základy a aplikace . London Mathematical Society Lecture Note Series. 251 . Cambridge University Press. s. 535–545. ISBN 978-0-521-63298-0.
• Buchberger, Bruno; Kauers, Manuel (2010). „Gröbnerovy základny“ . Scholarpedia . 5 (10): 7763. doi : 10,4249/scholarpedia.7763 .
• Fröberg, Ralf (1997). Úvod do Gröbnerových základen . Wiley. ISBN 0-471-97442-0.
• Sturmfels, Bernd (listopad 2005). „Co je ... základna Gröbnera?“ (PDF) . Oznámení Americké matematické společnosti . 52 (10): 1199–1200, stručný úvodCS1 maint: postscript ( odkaz )
• Shirshov, Anatoliĭ I. (1999). „Určité algoritmické problémy pro Lieovy algebry“ (PDF) . Bulletin ACM SIGSAM . 33 (2): 3–6. doi : 10,1145/334714,334715 . S2CID  37070503 .(přeloženo ze Sibirsku. Mat. Zh. Siberian Mathematics Journal 3 (1962), 292–296).
• Aschenbrenner, Matthias ; Hillar, Christopher (2007). „Konečná generace symetrických ideálů“ . Transakce Americké matematické společnosti . 359 (11): 5171–92. doi : 10,1090/S0002-9947-07-04116-5 . S2CID  5656701 . (na nekonečně dimenzionálních Gröbnerových základnách pro polynomiální prstence v nekonečně mnoha neurčitých).

externí odkazy

• Faugèrova vlastní implementace jeho algoritmu F4
• „Gröbnerův základ“ , encyklopedie matematiky , EMS Press , 2001 [1994]
• Buchberger, B. (2003). „Gröbnerovy základy: Krátký úvod pro teoretiky systémů“ (PDF) . V Moreno-Diaz, R .; Buchberger, B .; Freire, J. (eds.). Teorie počítačových systémů - EUROCAST 2001: výběr příspěvků z 8. mezinárodního workshopu o teorii systémů podporovaných počítačem . Springer. s. 1–19. ISBN 978-3-540-45654-4.
• Buchberger, B .; Zapletal, A. „Bibliografie Gröbnerových základů“ .
• Stránka srovnávacích časování pro software Gröbner Bases
• Prof. Bruno Buchberger Bruno Buchberger
• Weisstein, Eric W. „Gröbnerův základ“ . MathWorld .
• Gröbnerův úvod do Scholarpedia