E ₇ (matematika) - E₇ (mathematics)

Algebraická struktura → Skupinová teorie Skupinová teorie
Základní pojmy Podskupina Normální podskupina Kvocientová skupina (Polo) přímý produkt Skupinové homomorfismy jádro obraz přímý součet produkt věnce jednoduchý konečný nekonečný kontinuální multiplikativní přísada cyklický Abelian vzepětí nilpotentní řešitelný Glosář teorie skupin Seznam témat teorie skupin
Konečné skupiny Klasifikace konečných jednoduchých skupin cyklický střídavý Typ lži sporadický Cauchyova věta Lagrangeova věta Sylowovy věty Hallova věta p-skupina Základní abelianská skupina Skupina Frobenius Multiplikátor Schur Symetrická skupina S n Kleinova čtyřskupina V Dihedral skupina D n Kvartérní skupina Q Dicyklická skupina Dic n
Diskrétní skupiny Mříže Celá čísla ( Z ) Zdarma skupina Modulární skupiny PSL (2, Z ) SL (2, Z ) Aritmetická skupina Mříž Hyperbolická skupina
Topologické a Lieovy skupiny Solenoid Kruh Obecné lineární GL ( n ) Speciální lineární SL ( n ) Ortogonální O ( n ) Euklidovský E ( n ) Speciální ortogonální SO ( n ) Unitary U ( n ) Speciální unitární SU ( n ) Symplectic Sp ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Konformní Difomorfismus Smyčka Nekonečná dimenzionální Lieova skupina O (∞) SU (∞) Sp (∞)
Algebraické skupiny Lineární algebraická skupina Redukční skupina Abelianská odrůda Eliptická křivka
proti t E

Lež skupiny
Klasické skupiny
Jednoduché Lie skupiny Klasický A n B č C č D č Výjimečný G 2 F 4 E 6 E 7 E 8
Další Lie skupiny Kruh Lorentz Poincaré Konformní skupina Difomorfismus Smyčka Euklidovský
Lež algebry
Poloplná Lieova algebra
Teorie reprezentace
Lež skupiny ve fyzice
Vědci Sophus Lie Henri Poincaré Wilhelm Killing Élie Cartan Hermann Weyl Claude Chevalley Harish-Chandra Armand Borel
Glosář Tabulka Lieových skupin
proti t E

V matematice je E ₇ název několika blízce příbuzných Lieových skupin , lineárních algebraických skupin nebo jejich Lieových algeber e ₇ , z nichž všechny mají rozměr 133; stejný zápis E ₇ se používá pro odpovídající kořenovou mřížku , která má hodnost  7. Označení E ₇ pochází z Cartan – Killing klasifikace složitých jednoduchých Lieových algeber , které spadají do čtyř nekonečných řad označených A _n , B _n , C _n , D _n a pět výjimečných případů označených E ₆ , E ₇ , E ₈ , F ₄ a G ₂ . Algebra E ₇ je tedy jedním z pěti výjimečných případů.

Základní skupinou (adjoint) komplexní formy, kompaktní reálné formy nebo jakékoli algebraické verze E ₇ je cyklická skupina Z / 2 Z a její vnější skupina automorfismu je triviální skupina . Rozměr jeho základního zastoupení je 56.

Skutečné a složité formy

K dispozici je unikátní komplex algebra lži typu E ₇ , odpovídající komplexní skupině komplexní rozměr 133. Komplex adjoint Lie skupina E ₇ z komplexu rozměru 133 může být považován za jednoduchý skutečné lži skupiny skutečného rozměru 266. To má zásadní skupina Z / 2 Z , má maximální kompaktní podskupinu kompaktní formy (viz níže) E ₇ a má vnější automorfickou skupinu řádu 2 generovanou komplexní konjugací.

Stejně jako komplexní Lieova skupina typu E ₇ existují čtyři reálné formy Lieovy algebry a odpovídající čtyři reálné formy skupiny s triviálním středem (všechny mají algebraický dvojitý kryt a tři z nich mají další ne -algebraické kryty, které dávají další skutečné formy), všechny skutečné dimenze 133, a to následovně:

• Kompaktní forma (což je obvykle ta, která je míněna, pokud nejsou uvedeny žádné další informace), která má základní skupinu Z / 2 Z a má triviální vnější automorfickou skupinu.
• Rozdělená forma, EV (nebo E _{7 (7)} ), která má maximální kompaktní podskupinu SU (8) / {± 1}, základní skupinu cyklickou řádu 4 a vnější skupinu automorfismu řádu 2.
• EVI (nebo E _{7 (-5)} ), která má maximální kompaktní podskupinu SU (2) · SO (12) / (uprostřed), základní skupinu necyklickou řádu 4 a triviální vnější automorfismus.
• EVII (nebo E _{7 (-25)} ), která má maximální kompaktní podskupinu SO (2) · E ₆ / (uprostřed), nekonečnou cyklickou základní skupinu a skupinu vnějšího automorfismu řádu 2.

Úplný seznam skutečných forem jednoduchých Lieových algeber najdete v seznamu jednoduchých Lieových skupin .

Kompaktní skutečná forma E ₇ je izometrická skupina 64-dimenzionálního výjimečného kompaktního Riemannova symetrického prostoru EVI (v Cartanově klasifikaci ). Je známá neformálně jako „ kvateroktonionová projektivní rovina “, protože ji lze sestavit pomocí algebry, která je tenzorovým součinem čtveřic a oktonionů , a je také známá jako Rosenfeldova projektivní rovina , i když se neřídí obvyklými axiomy projektivní rovina. To lze systematicky vidět pomocí konstrukce známé jako magický čtverec , a to díky Hansovi Freudenthalovi a Jacquesovi Titsovi .

Konstrukce Tits – Koecher produkuje formy algebry E ₇ Lie z algeber Albert, 27dimenzionálních výjimečných jordánských algeber .

E ₇ jako algebraická skupina

Prostřednictvím Chevalleyova základu pro Lieovu algebru lze definovat E ₇ jako lineární algebraickou skupinu nad celými čísly a následně nad jakýmkoli komutativním prstencem a zejména nad jakýmkoli polem: toto definuje takzvané rozdělení (někdy také známé jako „nekroucená“) adjunktní forma E ₇ . Nad algebraicky uzavřeným polem jsou toto a jeho dvojitý obal jediné formy; nad jinými poli však často existuje mnoho dalších forem nebo „zvratů“ E ₇ , které jsou klasifikovány v obecném rámci Galoisovy kohomologie (přes dokonalé pole k ) množinou H ¹ ( k , Aut (E ₇₎ )) který, protože Dynkinův diagram E ₇ (viz níže ) nemá žádné automorfismy, se shoduje s H ¹ ( k , E _{7, ad} ).

Přes pole reálných čísel se skutečná složka identity těchto algebraicky zkroucených forem E ₇ shoduje se třemi výše uvedenými skutečnými Lieovými skupinami , ale s jemností týkající se základní skupiny: všechny adjunktní formy E ₇ mají základní skupinu Z / 2 Z ve smyslu algebraické geometrie, což znamená, že připouštějí přesně jeden dvojitý obal; další nekompaktní reálné Lieovy grupové formy E ₇ proto nejsou algebraické a nepřipouštějí žádná věrná konečně-dimenzionální reprezentace.

Přes konečná pole znamená Lang – Steinbergova věta, že H ¹ ( k , E ₇ ) = 0, což znamená, že E ₇ nemá žádné zkroucené tvary: viz níže .

Algebra

Dynkinův diagram

Dynkin schéma pro E ₇ je dán .

Kořenový systém

126 vrcholy 2, ₃₁ mnohostěnu představují základních vektorů E ₇ , jak je uvedeno v tomto Coxeter rovina projekce
Coxeter-Dynkin schématu :

Zobrazeno v 3D projekci pomocí základních vektorů [u, v, w] poskytujících symetrii H3:
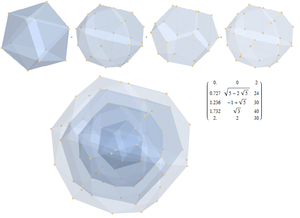
u = (1, φ , 0, -1, φ , 0,0)
v = ( φ , 0, 1, φ , 0, -1,0)
w = (0, 1, φ , 0, -1, φ , 0)
Předpokládaných 2 ₃₁ vrcholů mnohostěnů je seřazeno a sčítáno podle jejich 3D normy, která generuje stále průhlednější trupy každé sady sčítaných norem. Ty ukazují:
1) 2 body na počátku
2) 2 ikosahedrony
3) 1 icosadodecahedron
4) 2 dodecahedrony
5) 1 icosadodecahedron
pro celkem 126 vrcholů.

I když kořeny pokrývají 7-dimenzionální prostor, je symetrickější a pohodlnější je reprezentovat jako vektory ležící v 7-dimenzionálním podprostoru 8-dimenzionálního vektorového prostoru.

Kořeny jsou všech 8 × 7 permutací (1, −1,0,0,0,0,0,0) a všech permutací (½, ½, ½, ½, ½, −½, −½ , −½) ${\ displaystyle {\ begin {pmatrix} 8 \\ 4 \ end {pmatrix}}}$

Všimněte si, že 7-dimenzionální podprostor je podprostor, kde je součet všech osmi souřadnic nulový. Existuje 126 kořenů.

Tyto jednoduché kořeny jsou

(0, -1,1,0,0,0,0,0)

(0,0; -1,1,0,0,0,0)

(0,0,0, −1,1,0,0,0)

(0,0,0,0, −1,1,0,0)

(0,0,0,0,0, −1,1,0)

(0,0,0,0,0,0, −1,1)

(½, ½, ½, ½, ½, ½, ½, ½)

Jsou uvedeny tak, že jejich odpovídající uzly v Dynkinově diagramu jsou seřazeny zleva doprava (ve výše uvedeném diagramu) s posledním bočním uzlem.

Alternativní popis

Alternativní (7-rozměrný) popis kořenového systému, který je užitečný při zvažování E ₇ × SU (2) jako podskupiny E ₈ , je následující:

Všechny permutace (± 1, ± 1,0,0,0,0,0) zachovávající nulu při posledním vstupu, všechny následující kořeny se sudým počtem + ½ ${\ displaystyle 4 \ times {\ begin {pmatrix} 6 \\ 2 \ end {pmatrix}}}$

${\ displaystyle \ left (\ pm {1 \ nad 2}, \ pm {1 \ nad 2}, \ pm {1 \ nad 2}, \ pm {1 \ nad 2}, \ pm {1 \ nad 2} , \ pm {1 \ nad 2}, \ pm {1 \ nad {\ sqrt {2}}} \ vpravo)}$

a dva následující kořeny

${\ displaystyle \ left (0,0,0,0,0,0, \ pm {\ sqrt {2}} \ right).}$

Tak generátory se skládá z 66-dimenzionální SO (12) podalgebry, jakož i 64 generátory, které převádějí jako dva samostatně konjugát Weyl spinors z rotace (12) opačné chirality, a jejich chiralita generátoru a dvou dalších generátorů chiralities . ${\ displaystyle \ pm {\ sqrt {2}}}$

Vzhledem k E ₇ Cartanově matici (níže) a pořadí uzlů Dynkinova diagramu :

jedna volba jednoduchých kořenů je dána řádky následující matice:

${\ displaystyle {\ begin {bmatrix} 1 & -1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & -1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ - {\ frac {1} {2} {1} {2} } {2}} & - {\ frac {1} {2}} & - {\ frac {1} {2}} & - {\ frac {1} {2}} & - {\ frac {1} { 2}} & {\ frac {\ sqrt {2}} {2}} \\ 0 & 0 & 0 & 0 & 1 & -1 & 0 \\\ end {bmatrix}}.}$

Weylova skupina

Skupina Weyl E ₇ je řádu 2903040: je přímý produkt cyklické skupině řádu 2 a unikátní jednoduché skupině řádu 1451520 (který může být popsán jako PSP ₆ (2), nebo PSΩ ₇ (2)).

Kartanová matice

Hasseův diagram kořenového posetu E7 s popisky hran identifikující přidanou jednoduchou polohu kořene

${\ displaystyle {\ begin {bmatrix} 2 & -1 & 0 & 0 & 0 & 0 & 0 \\ - 1 & 2 & -1 & 0 & 0 & 0 & 0 \\ 0 & -1 & 2 & -1 & 0 & 0 & 0 \\ 0 & 0 & -1 & 2 & -1 & 0 & -1 \\ 0 & 0 & 0 & -1 & 2 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 a 0 1 a 0 a 0 a 2 \ end {bmatrix}}.}$

Důležité subalgebry a reprezentace

E ₇ má subalgebru SU (8), jak je zřejmé z poznámky, že v 8rozměrném popisu kořenového systému je první skupina kořenů identická s kořeny SU (8) (se stejnou kartanskou subalgebrou jako v E ₇ ).

Kromě 133 trojrozměrného adjoint reprezentace, je 56-rozměrný „vektor“ znázornění , které se nacházejí v E ₈ adjoint zastoupení.

Znaky konečných dimenzionálních reprezentací reálných a komplexních Lieových algeber a Lieových skupin jsou dány Weylovým vzorcem znaků . Rozměry nejmenších neredukovatelných reprezentací jsou (sekvence A121736 v OEIS ):

1 , 56, 133 , 912, 1463 , 1539 , 6480, 7371 , 8645 , 24320, 27664, 40755 , 51072, 86184, 150822 , 152152 , 238602 , 253935 , 293930 , 320112, 362880, 365750 , 573440 , 617253 , 861840, 885248, 915705 , 980343 , 2273920, 2282280, 2785552, 3424256 , 3635840 ...

Podtržené termíny ve výše uvedené posloupnosti jsou rozměry těchto neredukovatelných reprezentací, které vlastní adjunkční forma E ₇ (ekvivalentně těch, jejichž váhy patří do kořenové mřížky E ₇ ), zatímco celá sekvence dává rozměry neredukovatelných reprezentací jednoduše připojená forma E ₇ . Existuje neizomorfní neredukovatelné zastoupení dimenzí 1903725824, 16349520330 atd.

Tyto základní reprezentace jsou ty, s rozměry 133, 8645, 365750, 27664, 1539, 56 a 912 (odpovídající sedmi uzlů v diagramu Dynkin v předem určeném pořadí pro matrici Cartan výše, tj uzly jsou čteny ve šesti- řetězec uzlů jako první, přičemž poslední uzel je připojen ke třetímu).

E ₇ Polynomiální invarianty

E ₇ je skupina automorfismu následující dvojice polynomů v 56 nekomutativních proměnných. Rozdělíme proměnné do dvou skupin po 28, ( p , P ) a ( q , Q ), kde p a q jsou skutečné proměnné a P a Q jsou 3 × 3 oktonionové hermitovské matice. Pak první invariant je symplektický invariant Sp (56, R ):

${\ displaystyle C_ {1} = pq-qp + Tr [PQ] -Tr [QP]}$

Druhým komplikovanějším invariantem je symetrický kvartický polynom:

${\ displaystyle C_ {2} = (pq + Tr [P \ circ Q]) ^ {2} + pTr [Q \ circ {\ tilde {Q}}] + qTr [P \ circ {\ tilde {P}} ] + Tr [{\ tilde {P}} \ circ {\ tilde {Q}}]}$

Kde a operátor binárního kruhu je definován . ${\ displaystyle {\ tilde {P}} \ equiv \ det (P) P ^ {- 1}}$${\ displaystyle A \ circ B = (AB + BA) / 2}$

Alternativní kvartický polynomický invariant vytvořený Cartanem používá dvě anti-symetrické matice 8x8, každá s 28 komponentami.

${\ displaystyle C_ {2} = Tr [(XY) ^ {2}] - {\ dfrac {1} {4}} Tr [XY] ^ {2} + {\ frac {1} {96}} \ epsilon _ {ijklmnop} \ left (X ^ {ij} X ^ {kl} X ^ {mn} X ^ {op} + Y ^ {ij} Y ^ {kl} Y ^ {mn} Y ^ {op} \ right )}$

Skupiny Chevalley typu E ₇

Body nad konečným polem s q prvky (rozdělené) algebraické skupiny E ₇ (viz výše ), ať už adjungovaného (bez středů) nebo jednoduše spojeného tvaru (jeho algebraické univerzální pokrytí), dávají konečnou Chevalleyovu skupinu . To je úzce spojeno se skupinou napsanou E ₇ ( q ), nicméně v této notaci je dvojznačnost, která může znamenat několik věcí:

• konečná skupina skládající se z bodů nad F _q jednoduše spojené formy E ₇ (pro přehlednost to lze napsat E _{7, sc} ( q ) a je známá jako „univerzální“ Chevalleyova skupina typu E ₇ nad F _q ),
• (zřídka) konečná skupina skládající se z bodů nad F _q adjungovaného tvaru E ₇ (pro přehlednost to lze napsat E _{7, ad} ( q ) a je známá jako „adjunkční“ Chevalleyova skupina typu E ₇ nad F _q ), nebo
• konečná skupina, která je obrazem přirozené mapy od první k druhé: toto bude v následujícím textu označeno E ₇ ( q ), jak je to nejběžnější v textech zabývajících se konečnými skupinami.

Z pohledu konečné skupiny lze vztah mezi těmito třemi skupinami, který je zcela analogický vztahu mezi SL ( n , q ), PGL ( n , q ) a PSL ( n , q ), shrnout následovně: E ₇ ( q ) je jednoduchý pro libovolné q , E _{7, sc} ( q ) je jeho Schurův obal a E _{7, ad} ( q ) leží v jeho automorfické skupině; dále, když q je síla 2, všechny tři se shodují, a jinak (když q je liché) je Schurův multiplikátor E ₇ ( q ) 2 a E ₇ ( q ) má index 2 v E _{7, ad} ( q ), což vysvětluje, proč jsou E _{7, sc} ( q ) a E _{7, ad} ( q ) často psány jako 2 · E ₇ ( q ) a E ₇ ( q ) · 2. Z pohledu algebraické skupiny je méně běžné, že E ₇ ( q ) odkazuje na konečnou jednoduchou skupinu, protože ta není přirozeným způsobem množina bodů algebraické skupiny nad F _q na rozdíl od E _{7, sc} ( q ) a E7 _{, ad} ( q ).

Jak již bylo zmíněno výše, E ₇ ( q ) je jednoduché pro libovolné q a představuje jednu z nekonečných rodin oslovených klasifikací konečných jednoduchých skupin . Jeho počet prvků je dán vzorcem (sekvence A008870 v OEIS ):

${\ displaystyle {\ frac {1} {\ mathrm {gcd} (2, q-1)}} q ^ {63} (q ^ {18} -1) (q ^ {14} -1) (q ^ {12} -1) (q ^ {10} -1) (q ^ {8} -1) (q ^ {6} -1) (q ^ {2} -1)}$

Pořadí E _{7, sc} ( q ) nebo E _{7, ad} ( q ) (obě jsou stejná) lze získat odstraněním dělicího faktoru gcd (2, q −1) (sekvence A008869 v OEIS ). Schurův multiplikátor E ₇ ( q ) je gcd (2, q −1) a jeho vnější skupina automorfismu je produktem diagonální skupiny automorfismu Z / gcd (2, q −1) Z (dané působením E _{7, ad} ( q )) a skupina polních automatorfismů (tj. Cyklická řádu f, pokud q = p ^f, kde p je prvočíslo).

Důležitost ve fyzice

N = 8 supergravitace ve čtyřech rozměrech, což je dimenzionální redukce z 11 dimenzionální supergravitace, připouští bosonickou globální symetrii E ₇ a bosonickou lokální symetrii SU (8) . Fermiony jsou v reprezentacích SU (8), pole měřidla jsou v reprezentaci E ₇ a skaláry jsou v reprezentaci obou (gravitony jsou singlety vzhledem k oběma). Fyzikální stavy jsou v reprezentacích cosetu E ₇ / SU (8) .

V teorii strun se E ₇ jeví jako součást skupiny měřidel jedné z (nestabilních a nesymetrických ) verzí heterotické struny . Může se také objevit v neporušené skupině měřidel E ₈ × E ₇ v šestrozměrných zhutněních teorie heterotických strun, například na čtyřrozměrném povrchu K3 .

Viz také

• En (Lie algebra)
• Klasifikace ADE
• Seznam jednoduchých Lieových skupin

Poznámky

Reference

• Adams, J. Frank (1996), Přednášky o výjimečných Lieových skupinách , Chicago Přednášky z matematiky, University of Chicago Press , ISBN   978-0-226-00526-3 , MR   1428422
• John Baez , The Octonions , Oddíl 4.5: E ₇ , Bull. Amer. Matematika. Soc. 39 (2002), 145-205 . Online verze HTML na adrese http://math.ucr.edu/home/baez/octonions/node18.html .
• E. Cremmer a B. Julia, N = 8 supergravity teorie. 1. Lagrangian , Phys.Lett. B80: 48, 1978. Online naskenovaná verze na http://ac.els-cdn.com/0370269378903039/1-s2.0-0370269378903039-main.pdf?_tid=79273f80-539d-11e4-a133-00000aab0f6c&acdnat=1413289833_5f3539a6365149b108ddcec889200964 .