Modulární skupina - Modular group

Algebraická struktura → Skupinová teorie Skupinová teorie
Základní pojmy Podskupina Normální podskupina Kvocientová skupina (Polo) přímý produkt Skupinové homomorfismy jádro obraz přímý součet produkt věnce jednoduchý konečný nekonečný kontinuální multiplikativní přísada cyklický Abelian vzepětí nilpotentní řešitelný akce Glosář teorie skupin Seznam témat teorie skupin
Konečné skupiny Klasifikace konečných jednoduchých skupin cyklický střídavý Typ lži sporadický Cauchyova věta Lagrangeova věta Sylowovy věty Hallova věta p-skupina Základní abelianská skupina Skupina Frobenius Multiplikátor Schur Symetrická skupina S n Kleinova čtyřskupina V Dihedral skupina D n Čtveřice skupina Q Dicyklická skupina Dic n
Diskrétní skupiny Mříže Celá čísla ( )${\ displaystyle \ mathbb {Z}}$ Zdarma skupina Modulární skupiny PSL (2, )${\ displaystyle \ mathbb {Z}}$ SL (2, )${\ displaystyle \ mathbb {Z}}$ Aritmetická skupina Mříž Hyperbolická skupina
Topologické a Lieovy skupiny Solenoid Kruh Obecné lineární GL ( n ) Speciální lineární SL ( n ) Ortogonální O ( n ) Euklidovský E ( n ) Speciální ortogonální SO ( n ) Unitary U ( n ) Speciální unitární SU ( n ) Symplectic Sp ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Konformní Difomorfismus Smyčka Nekonečná dimenzionální Lieova skupina O (∞) SU (∞) Sp (∞)
Algebraické skupiny Lineární algebraická skupina Redukční skupina Abelianská odrůda Eliptická křivka
proti t E

V matematiky je modulární skupina je projektivní zvláštní lineární skupina PSL (2, Z ) na 2 x 2 matic s celočíselnými koeficienty a determinant 1. Matice a - jsou identifikovány. Modulární skupina působí na horní polovinu v komplexní rovině o frakční lineární transformace , a název „modulární skupina“ pochází z vztahu k moduli prostorů a není z modulární aritmetiky .

Definice

Modulární skupina Γ je skupina z lineárních dílčích transformací v horní polovině komplexní roviny , které mají formu

${\ displaystyle z \ mapsto {\ frac {az + b} {cz + d}},}$

kde a , b , c , d jsou celá čísla a ad - bc = 1 . Skupinová operace je složení funkce .

Tato skupina transformací je izomorfní s projektivní speciální lineární skupinou PSL (2, Z ) , což je podíl dvojrozměrné speciální lineární skupiny SL (2, Z ) nad celými čísly podle jejího středu { I , - I } . Jinými slovy, PSL (2, Z ) se skládá ze všech matic

${\ displaystyle {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}}}$

kde a , b , c , d jsou celá čísla, ad - bc = 1 a dvojice matic A a - A jsou považovány za identické. Skupinová operace je obvyklé násobení matic .

Někteří autoři definují modulární skupinu jako PSL (2, Z ) a další definují modulární skupinu jako větší skupinu SL (2, Z ) .

Některé matematické vztahy vyžadují zvážení skupiny GL (2, Z ) matic s determinantem plus nebo minus jedna. ( SL (2, Z ) je podskupinou této skupiny.) Podobně PGL (2, Z ) je kvocientová skupina GL (2, Z ) / { I , - I } . 2 x 2 matrice se jednotkou determinantou je symplectic matice , a tím SL (2, Z ) = Sp (2, Z ) se symplectic skupina o 2 x 2 matice.

Hledání prvků

Aby bylo možné najít explicitní prvky v SL (2, Z ) , existuje trik, který vezme dvě celá čísla coprime a vloží je do matice${\ displaystyle a, b}$

${\ displaystyle {\ begin {pmatrix} a & x \\ b & y \ end {pmatrix}}}$

a řešení determinantní rovnice

${\ displaystyle ay-bx = 1}$

Všimněte si determinant rovnice síly být coprime, protože jinak by být faktorem tak, aby , , tedy${\ displaystyle a, b}$${\ displaystyle c}$${\ displaystyle ca '= a}$${\ displaystyle cb '= b}$

${\ displaystyle c (a'y-b'x) = 1}$

nebude mít celočíselná řešení. Například pokud se pak přečte determinantní rovnice${\ displaystyle a = 7, {\ text {}} b = 6}$

${\ displaystyle 7y-6x = 1}$

pak brát a dávat , tedy${\ displaystyle y = -5}$${\ displaystyle x = -6}$${\ displaystyle -35 - (- 36) = 1}$

${\ displaystyle {\ begin {pmatrix} 7 & -6 \\ 6 & -5 \ end {pmatrix}}}$

je matice. Poté pomocí projekce tyto matice definují prvky v PSL (2, Z ) .

Číselně-teoretické vlastnosti

Jednotkový determinant

${\ displaystyle {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}}}$

znamená, že zlomky _A/b, _A/C, _C/d, _b/djsou všechny neredukovatelné, což nemá žádné společné faktory (samozřejmě za předpokladu, že jmenovatelé jsou nenuloví). Obecněji, pokudp/q je tedy neredukovatelná frakce

${\ displaystyle {\ frac {ap + bq} {cp + dq}}}$

je také neredukovatelné (opět za předpokladu, že jmenovatel bude nenulový). Tímto způsobem lze spojit jakoukoli dvojici neredukovatelných frakcí; to znamená pro jakýkoli párp/q a r/s z neredukovatelných frakcí existují prvky

${\ displaystyle {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}} \ in \ operatorname {SL} (2, \ mathbf {Z})}$

takhle

${\ displaystyle r = ap + bq \ quad {\ mbox {a}} \ quad s = cp + dq.}$

Prvky modulární skupiny poskytují symetrii na dvojrozměrné mřížce . Nechť ω ₁ a ω ₂ jsou dvě komplexní čísla, jejichž poměr není reálný. Pak sada bodů

${\ displaystyle \ Lambda (\ omega _ {1}, \ omega _ {2}) = \ {m \ omega _ {1} + n \ omega _ {2}: m, n \ in \ mathbf {Z} \ }}$

je mřížka rovnoběžníků v rovině. Odlišný pár vektorů α ₁ a α ₂ vygeneruje přesně stejnou mřížku tehdy a jen tehdy

${\ displaystyle {\ begin {pmatrix} \ alpha _ {1} \\\ alpha _ {2} \ end {pmatrix}} = {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}} {\ begin { pmatrix} \ omega _ {1} \\\ omega _ {2} \ end {pmatrix}}}$

pro nějakou matici v GL (2, Z ) . Z tohoto důvodu mají dvojnásobně periodické funkce , jako jsou eliptické funkce , symetrii modulárních skupin.

Působení modulární skupiny na racionální čísla lze nejsnadněji pochopit představou čtvercové mřížky, přičemž mřížkový bod ( p , q ) odpovídá zlomkup/q(viz Euklidův sad ). Neredukovatelná frakce je ta, která je viditelná z původu; působení modulární skupiny na zlomek nikdy nebere viditelnou (neredukovatelnou) na skrytou (redukovatelnou) a naopak.

Všimněte si, že kterýkoli člen modulární skupiny mapuje projektivně prodlouženou skutečnou linii jedna k jedné a dále bijektivně mapuje projektivně prodlouženou racionální linii (racionální s nekonečnem) na sebe, iracionální na iracionální, transcendentní čísla na transcendentální čísla, nerealistická čísla k nerealistickým číslům, horní polorovina k horní polorovině atd.

Li p _{n -1}/q _{n -1} a p _n/q _njsou dva po sobě jdoucí konvergenty spojitého zlomku , pak matice

${\ displaystyle {\ begin {pmatrix} p_ {n-1} & p_ {n} \\ q_ {n-1} & q_ {n} \ end {pmatrix}}}$

patří GL (2, Z ) . Zejména pokud bc - ad = 1 pro kladná celá čísla a , b , c , d s a < b a c < d pakA/b a C/dbudou sousedé v sekvenci Farey řádu max ( b , d ) . Mezi důležité speciální případy pokračujících konvertorů zlomků patří Fibonacciho čísla a řešení Pellovy rovnice . V obou případech, čísla mohou být uspořádány pro vytvoření pologrupa podmnožinu modulární skupiny.

Skupinové teoretické vlastnosti

Prezentace

Je možné ukázat, že modulární skupina je generována dvěma transformacemi

${\ displaystyle {\ begin {zarovnáno} S &: z \ mapsto - {\ frac {1} {z}} \\ T &: z \ mapsto z + 1 \ end {zarovnáno}}}$

tak, že každý prvek v modulárním může znamenat skupinu (v non-jedinečným způsobem) složením pravomocí S a T . Geometricky, S představuje inverzi v jednotkové kružnici následovanou odrazem vzhledem k imaginární ose, zatímco T představuje jednotkový překlad doprava.

Generátory S a T dodržují vztahy S ² = 1 a ( ST ) ³ = 1 . Je možné ukázat, že se jedná o kompletní sadu vztahů, takže modulární skupina má prezentaci :

${\ displaystyle \ Gamma \ cong \ left \ langle S, T \ mid S ^ {2} = I, \ left (ST \ right) ^ {3} = I \ right \ rangle}$

Tato prezentace popisuje modulární skupinu jako rotační trojúhelníkovou skupinu D (2, 3, ∞) (nekonečno, protože na T neexistuje žádný vztah ), a proto se mapuje na všechny trojúhelníkové skupiny (2, 3, n ) přidáním relace T ⁿ = 1 , který se vyskytuje například v podskupině shody ru ( n ) .

Pomocí generátory S a ST místo S a T , to ukazuje, že modulární skupina je isomorphic k volné produktu z cyklických skupin, C ₂ a C ₃ :

${\ displaystyle \ Gamma \ cong C_ {2} * C_ {3}}$

• 

  Působení T  : z ↦ z + 1 na H

• 

  Působení S  : z ↦ -1/zna H

Prýmek skupina

Cop skupina B ₃ je univerzální centrální rozšíření modulového skupiny, s těmito sedí jako latexy uvnitř (topologické) univerzální krycí skupiny SL ₂ ( R ) → PSL ₂ ( R ) . Dále modulární skupina má triviální centrum, a tím i modulární skupina je isomorphic k kvocientu skupiny z B ₃ modulo jeho střed ; ekvivalentně do skupiny vnitřních automorphisms z B ₃ .

Opletení skupina B ₃ je zase izomorfní k uzlu skupiny v trojlístku uzlu .

Kvocienty

Kvocienty kongruenčních podskupin jsou velmi zajímavé.

Dalšími důležitými kvocienty jsou (2, 3, n ) skupiny trojúhelníků, které geometricky odpovídají sestupu k válci, kvocienty x souřadnic modulo n , jako T ⁿ = ( z ↦ z + n ) . (2, 3, 5) je skupina ikosahedrální symetrie a skupina (2, 3, 7) trojúhelníků (a související obklady) je obalem všech Hurwitzových povrchů .

Prezentace jako skupina matic

Skupinu lze generovat dvěma maticemi ${\ displaystyle {\ text {SL}} _ {2} (\ mathbb {Z})}$

${\ displaystyle S = {\ begin {pmatrix} 0 & -1 \\ 1 & 0 \ end {pmatrix}}, {\ text {}} T = {\ begin {pmatrix} 1 & 1 \\ 0 & 1 \ end {pmatrix}}}$

od té doby

${\ displaystyle S ^ {2} = - I_ {2}, {\ text {}} (ST) ^ {3} = {\ begin {pmatrix} 0 & -1 \\ 1 & 1 \ end {pmatrix}} ^ {3 } = - I_ {2}}$

Projekce promění tyto matice na generátory se vztahy podobnými skupinové prezentaci. ${\ displaystyle {\ text {SL}} _ {2} (\ mathbb {Z}) \ do {\ text {PSL}} _ {2} (\ mathbb {Z})}$${\ displaystyle {\ text {PSL}} _ {2} (\ mathbb {Z})}$

Vztah k hyperbolické geometrii

Modulární skupina je důležité, protože to tvoří podskupinu této skupiny isometries z hyperbolického letadla . Pokud vezmeme v úvahu horní polorovina modelu H hyperbolického planimetrie, pak skupina všech orientace zachovávajících isometries z H se skládá ze všech Möbius transformací formuláře

${\ displaystyle z \ mapsto {\ frac {az + b} {cz + d}}}$

kde a , b , c , d jsou reálná čísla . Pokud jde o projektivní souřadnice , skupina PSL (2, R ) působí na horní polorovinu H projektivitou:

${\ displaystyle [z, \ 1] {\ begin {pmatrix} a & c \\ b & d \ end {pmatrix}} \, = \, [az + b, \ cz + d] \, \ thicksim \, \ left [{ \ frac {az + b} {cz + d}}, \ 1 \ right].}$

Tato akce je věrná . Vzhledem k tomu, PSL (2, Z ), je podskupina PSL (2, R ) , modulární skupina je podskupinou skupiny orientace zachovávajících isometries z H .

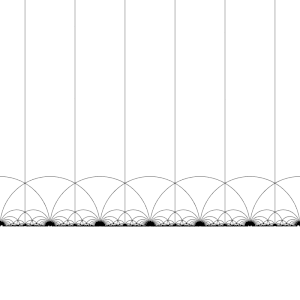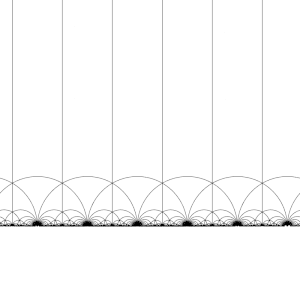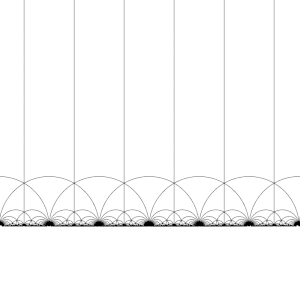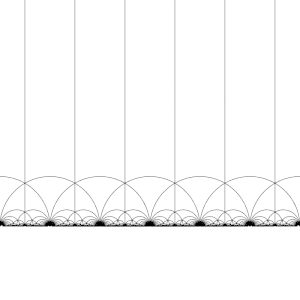
Teselace hyperbolické roviny

Modulární skupina Γ působí na H jako diskrétní podskupiny z PSL (2, R ) , který je pro každou z, v H najdeme sousedství Z , která neobsahuje žádný jiný prvek oběžné dráhy o Z . To také znamená, že můžeme zkonstruovat základní domény , které se (zhruba) obsahují právě jeden zástupce z oběžné dráhy každé Z v H . (Je nutná opatrnost na hranici domény.)

Existuje mnoho způsobů konstrukce základní domény, ale běžnou volbou je region

${\ displaystyle R = \ left \ {z \ in \ mathbf {H} \ colon \ left | z \ right |> 1, \, \ left | \, {\ mbox {Re}} (z) \, \ right | <{\ tfrac {1} {2}} \ doprava \}}$

ohraničený svislými čarami Re ( z ) =1/2a Re ( z ) = -1/2a kruh | z | = 1 . Tato oblast je hyperbolický trojúhelník. Má vrcholy v1/2+ i√ 3/2a -1/2+ i√ 3/2, kde je úhel mezi jeho stranami π/3a třetí vrchol v nekonečnu, kde úhel mezi jeho stranami je 0.

Transformací této oblasti postupně každým z prvků modulární skupiny se vytvoří pravidelná mozaikování hyperbolické roviny kongruentními hyperbolickými trojúhelníky známými jako V6.6. Triang Vytvoří se trojúhelníkové obklady nekonečného řádu . Všimněte si, že každý takový trojúhelník má jeden vrchol buď v nekonečnu, nebo na skutečné ose Im ( z ) = 0 . Tento obklad lze rozšířit na Poincarého disk , kde každý hyperbolický trojúhelník má jeden vrchol na hranici disku. Dlaždice Poincarého disku je dána přirozeným způsobem J -invariantem , který je neměnný pod modulární skupinou a dosahuje každého komplexního čísla jednou v každém trojúhelníku těchto oblastí.

Tuto mozaikování lze mírně vylepšit rozdělením každé oblasti na dvě poloviny (konvenčně zbarvené černé a bílé) přidáním mapy orientující obrácení; barvy pak odpovídají orientaci domény. Přidáním ( x , y ) ↦ (- x , y ) a převzetím pravé poloviny oblasti R (kde Re ( z ) ≥ 0 ) se získá obvyklá mozaikování. Tato mozaikování se poprvé objevuje v tisku ( Klein & 1878 / 79a ), kde je připisována Richardu Dedekindovi v odkazu na ( Dedekind 1877 ).

Mapu skupin (2, 3, ∞) → (2, 3, n ) (od modulární skupiny po trojúhelníkovou skupinu) lze vizualizovat z hlediska tohoto obkladu (čímž se získá obklad na modulární křivce), jak je znázorněno na videu vpravo.

Paracompact uniformní obklady v rodině [∞, 3] proti t E
Symetrie: [∞, 3], (* ∞32)							[∞, 3] + (∞32)	[1 + , ∞, 3] (* ∞33)		[∞, 3 + ] (3 * ∞)
		=	=	=				= nebo	= nebo	=
{∞, 3}	t {∞, 3}	r {∞, 3}	t {3, ∞}	{3, ∞}	rr {∞, 3}	tr {∞, 3}	sr {∞, 3}	h {∞, 3}	h 2 {∞, 3}	s {3, ∞}
Jednotné duály
V∞ 3	V3.∞.∞	V (3.∞) 2	V6.6.∞	V3 ∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V (3.∞) 3		V3.3.3.3.3.∞

Podskupiny shody

Důležité podskupiny modulární skupiny Γ , nazývané kongruenční podskupiny , jsou dány uložením kongruenčních vztahů na přidružené matice.

K dispozici je přírodní homomorphism SL (2, Z ) → SL (2, Z / N Z ) vzhledem k tomu, že budou odstraněny položky modulo N . To indukuje homomorfismus na modulární skupině PSL (2, Z ) → PSL (2, Z / N Z ) . Jádro tohoto homomorfismu se nazývá hlavní kongruenci podskupinu z hladiny N , označený Γ ( N ) . Máme následující krátkou přesnou sekvenci :

${\ Displaystyle 1 \ až \ Gamma (N) \ až \ Gamma \ až {\ mbox {PSL}} (2, \ mathbf {Z} / N \ mathbf {Z}) \ až 1}$.

Být jádrem homomorfismu Γ ( N ) je normální podskupina modulární skupiny Γ . Skupina Γ ( N ) je dána jako množina všech modulárních transformací

${\ displaystyle z \ mapsto {\ frac {az + b} {cz + d}}}$

pro které a ≡ d ≡ ± 1 (mod N ) a b ≡ c ≡ 0 (mod N ) .

Je snadné ukázat, že stopa matice představující prvek Γ ( N ) nemůže být −1, 0 nebo 1, takže tyto podskupiny jsou skupiny bez zkroucení . (Existují i ​​další podskupiny bez kroucení.)

Hlavní podskupina shody úrovně 2, Γ (2) , se také nazývá modulární skupina Λ . Protože PSL (2, Z / 2 Z ) je izomorfní s S ₃ , Λ je podskupina indexu 6. Skupina Λ se skládá ze všech modulárních transformací, pro které jsou a a d sudá a b a c jsou sudá.

Další důležitou rodinou podskupin kongruence je modulární skupina Γ ₀ ( N ) definovaná jako množina všech modulárních transformací, pro které c ≡ 0 (mod N ) , nebo ekvivalentně, jako podskupina, jejíž matice se po redukci modulo N stanou horními trojúhelníky . Všimněte si, že Γ ( N ) je podskupina Γ ₀ ( N ) . Tyto modulární křivky spojené s těmito skupinami jsou aspektem obrovského měsíčního svitu - pro prvočíslo p , modulární křivka normalizátor je rod nula tehdy, když p rozděluje pořadí ze skupiny monster , nebo ekvivalentně, pokud p je supersingular prime .

Dyadický monoid

Jedním z důležitých podmnožina modulární skupiny je dyadická monoid , který je monoid všech řetězců formuláře ST ^k ST ^m ST ⁿ ... pro pozitivní celá čísla k , m , n , ... . Tento monoid se přirozeně vyskytuje ve studiu fraktální křivek a popisuje sebepodobnosti symetrie z funkce Cantor , Minkowského funkce otazníku , a Koch sněhová vločka , z nichž každý je zvláštní případ obecného de Rham křivky . Monoid má také výškově lineární reprezentace; například reprezentaci N = 3 lze chápat tak, že popisuje autosymetrii křivky blancmange .

Mapy torusu

Skupina GL (2, Z ) je lineární mapa zachovávající standardní mřížku Z ² a SL (2, Z ) je mapa zachovávající orientaci zachovávající tuto mříž; že tedy sestoupit do vlastních homeomorphisms na anuloidu (SL mapování orientace-chránit mapy), a v mapě skutečnosti isomorphically k (rozšířené) mapování třídy skupiny na torus, což znamená, že každý self-homeomorphism of torus je izotopový do A mapa tohoto formuláře. Algebraické vlastnosti matice jako prvku GL (2, Z ) odpovídají dynamice indukované mapy torusu.

Hecke skupiny

Modulární skupinu lze zobecnit na Heckeovy skupiny , pojmenované pro Ericha Heckeho , a definovat je následovně.

Hecke skupina H _q s q ≥ 3 , je diskrétní skupina generovaná

${\ displaystyle {\ begin {zarovnáno} z & \ mapsto - {\ frac {1} {z}} \\ z & \ mapsto z + \ lambda _ {q}, \ end {zarovnáno}}}$

kde λ _q = 2 cosπ/q. Pro malé hodnoty q ≥ 3 má jeden:

${\ displaystyle {\ begin {zarovnáno} \ lambda _ {3} & = 1, \\\ lambda _ {4} & = {\ sqrt {2}}, \\\ lambda _ {5} & = {\ frac {1 + {\ sqrt {5}}} {2}}, \\\ lambda _ {6} & = {\ sqrt {3}}, \\\ lambda _ {8} & = {\ sqrt {2+ {\ sqrt {2}}}}. \ end {zarovnáno}}}$

Modulární skupina Γ je izomorfní H ₃ a sdílejí vlastnosti a použití - například tak, jak to má volný produkt z cyklických skupin

${\ displaystyle \ Gamma \ cong C_ {2} * C_ {3},}$

obecněji jeden má

${\ displaystyle H_ {q} \ cong C_ {2} * C_ {q},}$

což odpovídá trojúhelníkové skupině (2, q , ∞) . Podobně existuje představa o podskupinách hlavní kongruence spojené s hlavními ideály v Z [ λ ] .

Dějiny

Modulární skupinu a její podskupiny nejprve podrobně studoval Richard Dedekind a Felix Klein jako součást svého programu Erlangen v 70. letech 19. století. Úzce související eliptické funkce však studoval Joseph Louis Lagrange v roce 1785 a další výsledky týkající se eliptických funkcí publikovali Carl Gustav Jakob Jacobi a Niels Henrik Abel v roce 1827.

Viz také

Reference