Antiprism - Antiprism
| Sada uniformních n -gonálních antiprismů | |
|---|---|
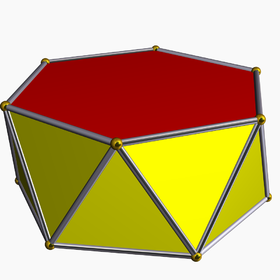 Příklad uniformního hexagonálního antiprismu |
|
| Typ | uniformní ve smyslu polopravidelného mnohostěnu |
| Tváře | 2 { n } + 2 n {3} |
| Hrany | 4 n |
| Vrcholy | 2 n |
| Conwayův polyhedronový zápis | A n |
| Konfigurace vrcholů | 3.3.3. n |
| Symbol Schläfli | {} ⊗ { n } s {2,2 n } sr {2, n } |
| Coxeterovy diagramy |
|
| Skupina symetrie | D n d , [2 + , 2 n ], (2* n ), pořadí 4 n |
| Rotační skupina | D n , [2, n ] + , (22 n ), pořadí 2 n |
| Duální mnohostěn | konvexní dvoj uniformní n -gonální lichoběžník |
| Vlastnosti | konvexní , vrcholně tranzitivní , pravidelné mnohoúhelníkové plochy, kongruentní a koaxiální báze |
| Síť |
 Příklad jednotné enneagonální antiprism sítě (n = 9) |
V geometrii , An n -gonal antiprism nebo n -antiprism je polyhedron složen ze dvou rovnoběžných přímých kopií (ne zrcadlové obrazy) produktu ve formě n -sided mnohoúhelníku , spojených střídavým pás 2 n trojúhelníků .
Antiprismy jsou podtřídou prismatoidů a jsou (degenerovaným) typem urážlivého mnohostěnu .
Antiprisms jsou podobné hranoly , s výjimkou, že základny jsou zkrouceny vůči sobě navzájem, a tím, že boční plochy (spojovací bází) jsou 2 n trojúhelníky, spíše než n čtyřúhelníků.
Správný antiprism
U antiprismu s pravidelnými základnami n -gon se obvykle uvažuje o případu, kdy jsou tyto dvě kopie stočeny o úhel180/n stupně.
Osa pravidelného mnohoúhelníku je přímka kolmá k rovině polygonu a ležící v polygonu středu.
Pro antiprism se shodnými pravidelnými základnami n-gon, stočenými o úhel180/nstupňů, větší pravidelnosti se dosáhne, pokud mají základny stejnou osu: jsou koaxiální ; tj. (pro nekoplanární základny): pokud je čára spojující středy základen kolmá na základní roviny. Potom se antiprism nazývá pravý antiprism a jeho 2 n boční plochy jsou rovnoramenné trojúhelníky.
Jednotný antiprism
Jednotný antiprism má dvě shodné pravidelné základní plochy n-gon a 2 n rovnostranné trojúhelníky jako boční plochy.
Uniformní antiprismy tvoří nekonečnou třídu vrcholně tranzitivních mnohostěnů, stejně jako uniformní hranoly. Pro n = 2 máme pravidelný čtyřstěn jako digonální antiprism (degenerovaný antiprism); pro n = 3 pravidelný osmistěn jako trojúhelníkový antiprism (nedegenerovaný antiprism).
Dual polyhedra z antiprisms jsou trapezohedra .
Existence antiprismů byla diskutována a jejich jméno vymyslel Johannes Kepler , i když je možné, že byly dříve známé Archimedesovi , protože splňují stejné podmínky na tvářích a na vrcholech jako archimédská tělesa .
| Antiprism název | Digonální antiprism | (Trigonální) Trojúhelníkový antiprism |
(Tetragonal) Náměstí antiprism |
Pentagonální antiprism | Šestihranný antiprism | Heptagonální antiprism | Osmiboký antiprism | Enneagonální antiprism | Dekongonální antiprism | Hendekagonální antiprism | Dodecagonální antiprism | ... | Apeirogonální antiprism |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mnohostěnný obrázek |
|
|
|
|
|
|
|
|
|
|
|
... | |
| Sférický obkladový obrázek |
|
|
|
|
|
|
|
Obraz obkládající rovinu |
|
||||
| Konfigurace vrcholů. | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ... | ∞.3.3.3 |
Schlegelovy diagramy
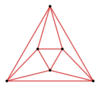 A3 |
 A4 |
 A5 |
 A6 |
 A7 |
 A8 |
Kartézské souřadnice
Kartézské souřadnice pro vrcholy pravého antiprismu (tj. S pravidelnými základnami n -gon a rovnoramennými bočními plochami) jsou
s k v rozmezí od 0 do 2 n - 1;
pokud jsou trojúhelníky rovnostranné, pak
Objem a povrch
Nechť a je hrana uniformního antiprismu; pak je hlasitost
a povrch je
Související mnohostěn
Existuje nekonečný soubor zkrácených antiprismů, včetně formy nižší symetrie zkráceného osmistěnu (zkrácený trojúhelníkový antiprism). Ty je možné střídat a vytvářet tak odpružené antiprismy , z nichž dva jsou Johnsonovy pevné látky , a urážlivý trojúhelníkový antiprism je forma nižší symetrie icosahedronu .
| Antiprismy | ||||
|---|---|---|---|---|

|

|

|

|
... |
| s {2,4} | s {2,6} | s {2,8} | s {2,10} | s {2,2 n } |
| Zkrácené antiprismy | ||||

|

|

|

|
... |
| ts {2,4} | ts {2,6} | ts {2,8} | ts {2,10} | ts {2,2n} |
| Snubní antiprismy | ||||
| J 84 | Icosahedron | J 85 | Nepravidelné tváře ... | |

|

|

|
|
... |
| ss {2,4} | ss {2,6} | ss {2,8} | ss {2,10} | ss {2,2n} |
Symetrie
Symetrie skupina na pravé n -antiprism (tj pravidelném základě a rovnoramenného boční plochy) je D n d žádání 4 n , s výjimkou případů:
- n = 2: pravidelný čtyřstěn , který má větší skupinu symetrie T d řádu 24 = 3 × (4 × 2), který má tři verze D 2d jako podskupiny;
- n = 3: pravidelný osmistěn , který má větší skupinu symetrie O h řádu 48 = 4 × (4 × 3), který má čtyři verze D 3d jako podskupiny.
Skupina symetrie obsahuje inverzi právě tehdy, je -li n liché.
Skupina otáčení je D n řádu 2 n , s výjimkou případů:
- n = 2: pravidelný čtyřstěn, který má větší rotační skupinu T řádu 12 = 3 × (2 × 2), který má tři verze D 2 jako podskupiny;
- n = 3: pravidelný osmistěn, který má větší rotační skupinu O řádu 24 = 4 × (2 × 3), který má čtyři verze D 3 jako podskupiny.
Hvězdný antiprism
 5/2-antiprism |
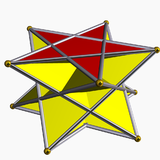 5/3-antiprism |
||||
 9/2-antiprism |
 9/4-antiprism |
 9/5-antiprism |
|||
Jednotné hvězdné antiprismy jsou pojmenovány podle svých hvězdných polygonových základen { p / q } a existují v programových a retrográdních (zkřížených) roztocích. Zkřížené tvary mají protínající se vrcholové figury a jsou označeny „převrácenými“ zlomky: p / ( p - q ) místo p / q ; příklad: 5/3 místo 5/2.
Přímo hvězda antiprism má dvě shodné koaxiální pravidelné konvexní nebo hvězda polygon základní plochy, a 2 n rovnoramenný trojúhelník boční plochy.
Jakýkoli hvězdný antiprism s pravidelnými konvexními nebo hvězdicovými mnohoúhelníkovými základy může být vytvořen jako pravý hvězdný antiprism (překladem a/nebo zkroucením jedné ze svých základen, je -li to nutné).
V retrográdních formách, ale ne v prográdních formách, trojúhelníky spojující konvexní nebo hvězdicové základny protínají osu rotační symetrie. Tím pádem:
- Retrográdní hvězdicové antihrany s pravidelnými konvexními mnohoúhelníkovými základnami nemohou mít všechny stejné délky hran, takže nemohou být jednotné. "Výjimka": retrográdní hvězdný antiprism s rovnostrannými trojúhelníkovými základy (konfigurace vrcholů: 3.3/2.3.3) může být jednotný; ale pak má vzhled rovnostranného trojúhelníku: je to degenerovaný hvězdicový mnohostěn.
- Podobně některé retrográdní hvězdné antiprismy s pravidelnými hvězdicovými mnohoúhelníkovými základnami nemohou mít všechny stejné délky hran, takže nemohou být jednotné. Příklad: retrográdní hvězdicový antiprism s pravidelnými hvězdicovými základnami 7/5-gon (konfigurace vrcholů: 3.3.3.7/5) nemůže být jednotný.
Rovněž mohou být zkonstruovány hvězdicové antiprismatické sloučeniny s pravidelnými hvězdicovými p / q -gonovými bázemi, pokud p a q mají společné faktory. Příklad: hvězda 10/4-antiprism je sloučenina dvou hvězd 5/2 antiprismů.
| Skupina symetrie | Jednotné hvězdy | Správné hvězdy | |||
|---|---|---|---|---|---|
| D 4d [2 + , 8] (2*4) |
 3.3/2.3.4 |
||||
| D 5h [2,5] (*225) |
 3.3.3.5/2 |
 3.3/2.3.5 |
|||
| D 5d [2 + , 10] (2*5) |
 3.3.3.5/3 |
||||
| D 6d [2 + , 12] (2*6) |
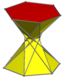 3.3/2.3.6 |
||||
| D 7h [2,7] (*227) |
 3.3.3.7/2 |
 3.3.3.7/4 |
|||
| D 7d [2 + , 14] (2*7) |
 3.3.3.7/3 |
||||
| D 8d [2 + , 16] (2*8) |
 3.3.3.8/3 |
 3.3.3.8/5 |
|||
| D 9h [2,9] (*229) |
 3.3.3.9/2 |
 3.3.3.9/4 |
|||
| D 9d [2 + , 18] (2*9) |
 3.3.3.9/5 |
||||
| D 10d [2 + , 20] (2*10) |
 3.3.3.10/3 |
||||
| D 11h [2,11] (*2.2.11) |
 3.3.3.11/2 |
 3.3.3.11/4 |
 3.3.3.11/6 |
||
| D 11d [2 + , 22] (2*11) |
 3.3.3.11/3 |
 3.3.3.11/5 |
 3.3.3.11/7 |
||
| D 12d [2 + , 24] (2*12) |
 3.3.3.12/5 |
 3.3.3.12/7 |
|||
| ... | ... | ||||
Viz také
- Apeirogonální antiprism
- Opravený antiprism
- Velký antiprism -čtyřrozměrný polytop
- One World Trade Center , budova sestávající převážně z protáhlého čtvercového antiprismu
- Zkosený polygon
Reference
- Anthony Pugh (1976). Polyhedra: Vizuální přístup . California: University of California Press Berkeley. ISBN 0-520-03056-7. Kapitola 2: Archimédský mnohostěn, prisma a antiprismy