Prýmková skupina - Braid group

V matematice je skupina opletení na n pramenech (označená ), také známá jako Artinova skupina opletení, skupina , jejíž prvky jsou třídami ekvivalence n- copánků (např. Pod izotopií okolí ) a jejichž skupinovou operací je složení copánků (viz § Úvod ). Příklady aplikací skupin copánků zahrnují teorii uzlů , kde jakýkoli uzel může být reprezentován jako uzavření určitých copánků (výsledek známý jako Alexandrova věta ); v matematické fyzice, kde Artin${\ displaystyle B_ {n}}$ Kanonická prezentace skupiny opletení odpovídá Yang-Baxterově rovnici (viz § Základní vlastnosti ); a v monodromy invarianty algebraické geometrie .

Úvod

V tomto úvodu nechť n = 4 ; zobecnění na jiné hodnoty n bude přímé. Zvažte dvě sady čtyř položek ležící na stole, přičemž položky v každé sadě jsou uspořádány ve svislé linii a takové, že jedna sada sedí vedle druhé. (Na obrázcích níže jsou to černé tečky.) Pomocí čtyř pramenů je každá položka první sady spojena s položkou druhé sady, takže je výsledkem vzájemné korespondence. Takové spojení se nazývá cop . Některá vlákna budou často muset přejít přes nebo pod ostatní, a to je zásadní: následující dvě spojení jsou různé copánky:

se liší od

Na druhé straně jsou dvě stejná opletení, která mohou vypadat stejně pomocí „tahání pramenů“, považována za stejný cop:

je stejné jako

Všechny prameny se musí pohybovat zleva doprava; uzly jako následující nejsou považovány za copánky:

není cop

Libovolné dva copánky lze skládat tak, že nakreslíme první vedle druhého, identifikujeme čtyři položky uprostřed a spojíme odpovídající prameny:

složený s

výnosy

Další příklad:

složený s

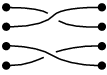
výnosy

Složení copánků σ a τ se píše jako στ .

Sada všech copánků na čtyřech pramenech je označena . Výše uvedené složení copánků je skutečně skupinová operace. Identita element je opletení se skládá ze čtyř rovnoběžných vodorovných pramenů, a inverzní z opletení se skládá z uvedeného opletu, který „zruší“ bez ohledu na první opletení udělal, který je získán tím, že proletí diagram, jako ty výše uvedené přes vertikální linii děje přes jeho střed. (První dva výše uvedené copánky jsou vzájemné inverze.) ${\ displaystyle B_ {4}}$

Aplikace

Teorie opletení byla nedávno aplikována na mechaniku tekutin , konkrétně na oblast chaotického míchání v tokech tekutin. Opletení (2 + 1) -dimenzionálních časoprostorových trajektorií vytvořených pohybem fyzických tyčí, periodických drah nebo „tyčí duchů“ a téměř invariantních sad bylo použito k odhadu topologické entropie několika inženýrských a přirozeně se vyskytujících tekutých systémů prostřednictvím použití klasifikace Nielsen – Thurston .

Další oblastí intenzivního výzkumu zahrnujícího skupiny copů a související topologické koncepty v kontextu kvantové fyziky je teorie a (domnělá) experimentální implementace tzv. Anyonů . Ty mohou nakonec skončit a vytvořit základ pro kvantové výpočty s korekcí chyb, takže jejich abstraktní studie má v současné době zásadní význam v kvantové informaci .

Formální léčba

K tomu, aby výše uvedený neformální diskusi o opletení skupin na pevném podkladu, je třeba použít homotopy pojem algebraické topologii , definuje prýmek skupiny jako základní skupiny jednoho prostoru konfigurace . Alternativně lze definovat skupinu opletení čistě algebraicky prostřednictvím vztahů opletení, přičemž obrázky budou mít na paměti pouze jako vodítko pro intuici.

Vysvětlit, jak snížit copu skupinu ve smyslu Artin do základní skupiny, považujeme připojeného potrubí o rozměru alespoň 2. symetrický produktu z kopií prostředku kvocient je násobně kartézský součin ze působením permutací na symetrické skupiny na prameny působí na indexy souřadnic. To znamená, že objednaný -tuple je na stejné oběžné dráze jako jakýkoli jiný, který je jeho re-objednanou verzí. ${\ displaystyle X}$${\ displaystyle n}$${\ displaystyle X}$${\ displaystyle X ^ {n}}$${\ displaystyle n}$${\ displaystyle X}$${\ displaystyle n}$${\ displaystyle n}$

Cesta v -fold symetrickém produktu je abstraktní způsob, jak diskutovat o bodech , považovaných za neuspořádaný -tuple, nezávisle trasování řetězců. Protože musíme požadovat, aby řetězce nikdy neprocházely navzájem, je nutné, abychom procházeli do podprostoru symetrického součinu, oběžných drah -tuples odlišných bodů. To znamená, že odstraníme všechny podprostory definované podmínkami pro všechny . Toto je neměnné pod symetrickou skupinou a je to kvocient podle symetrické skupiny nevyloučených n - tic. Podmínka dimenze bude připojena. ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle X}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle Y}$${\ displaystyle n}$${\ displaystyle X ^ {n}}$${\ displaystyle x_ {i} = x_ {j}}$${\ Displaystyle 1 \ leq já <j \ leq n}$${\ displaystyle Y}$${\ displaystyle n}$${\ displaystyle Y}$

S touto definicí pak můžeme skupinu copů s řetězci ${\ displaystyle X}$${\ displaystyle n}$ nazvat základní skupinou (pro jakoukoli volbu základního bodu - to je dobře definováno až po izomorfismus). Případ, kdy je euklidovská rovina, je původní z Artina. V některých případech to může být prokázáno, že vyšší homotopy skupiny o zanedbatelné. ${\ displaystyle Y}$${\ displaystyle X}$${\ displaystyle Y}$

Uzavřené copánky

Když X je rovina, opletení může být uzavřeno , tj. Odpovídající konce mohou být spojeny v párech, aby vytvořily spojení , tj. Možná propletené spojení případně vázaných smyček ve třech rozměrech. Počet komponent odkazu může být cokoli od 1 do n , v závislosti na permutaci pramenů určených odkazem. Věta JW Alexandra ukazuje, že každý odkaz lze získat tímto způsobem jako „uzavření“ copu. Porovnejte s řetězcovými odkazy .

Různá prýmky mohou vést ke stejnému odkazu, stejně jako různé diagramy křížení mohou vést ke stejnému uzlu . V roce 1935 popsal Andrey Markov ml. Dva tahy na diagramech opletení, které vedly k rovnocennosti v příslušných uzavřených copáncích. Verze s jediným tahem Markovovy věty byla publikována v roce 1997.

Vaughan Jones původně definoval svůj polynom jako invariant copu a poté ukázal, že to záviselo pouze na třídě uzavřeného copu.

Markov teorém poskytuje nezbytné a dostatečné podmínky, za kterých jsou uzávěry dvou provazců jsou ekvivalentní odkazy.

Index opletení

"Index copu" je nejmenší počet řetězců potřebných k vytvoření uzavřeného copu reprezentace odkazu. Rovná se nejmenšímu počtu Seifertových kruhů v jakékoli projekci uzlu.

Dějiny

Skupiny prýmků byly zavedeny výslovně Emilem Artinem v roce 1925, ačkoli (jak zdůraznil Wilhelm Magnus v roce 1974) již byly implicitní v práci Adolfa Hurwitze o monodromii z roku 1891.

Skupiny copů lze popsat explicitními prezentacemi , jak ukázal Emil Artin v roce 1947. Skupiny copů lze chápat také hlubší matematickou interpretací: jako základní skupina určitých konfiguračních prostorů .

Jak říká Magnus, Hurwitz podal interpretaci skupiny copů jako základní skupiny konfiguračního prostoru (srov. Teorie copů ), což byla interpretace, která byla ztracena z dohledu, dokud ji v roce 1962 znovu neobjevili Ralph Fox a Lee Neuwirth.

Základní vlastnosti

Generátory a vztahy

Zvažte následující tři copánky:

${\ displaystyle \ sigma _ {1}}$	${\ displaystyle \ sigma _ {2}}$	${\ displaystyle \ sigma _ {3}}$

Každý cop lze zapsat jako složení řady těchto copánků a jejich inverzí. Jinými slovy, tyto tři copánky generují skupinu . Chcete-li to vidět, je libovolný oplet skenován zleva doprava pro přechody; počínaje v horní části, kdykoli křížení vláken a se vyskytuje, nebo je snížena, v závislosti na tom, zda z pásů se pohybuje pod nebo nad řetězce . Po dosažení správného konce byl cop napsán jako produkt ‚s 'a jejich inverzí. ${\ displaystyle B_ {4}}$${\ displaystyle B_ {4}}$${\ displaystyle i}$${\ displaystyle i + 1}$${\ displaystyle \ sigma _ {i}}$${\ displaystyle \ sigma _ {i} ^ {- 1}}$${\ displaystyle i}$${\ displaystyle i + 1}$${\ displaystyle \ sigma}$

Je jasné že

(i) , ${\ displaystyle \ sigma _ {1} \ sigma _ {3} = \ sigma _ {3} \ sigma _ {1}}$

zatímco následující dva vztahy nejsou tak zjevné:

(iia) , ${\ displaystyle \ sigma _ {1} \ sigma _ {2} \ sigma _ {1} = \ sigma _ {2} \ sigma _ {1} \ sigma _ {2}}$

(IBIB) ${\ displaystyle \ sigma _ {2} \ sigma _ {3} \ sigma _ {2} = \ sigma _ {3} \ sigma _ {2} \ sigma _ {3}}$

(tyto vztahy nejlépe oceníte nakreslením copu na kousek papíru). Je možné ukázat, že všechny ostatní vztahy mezi copánky , a již vyplývá z těchto vztahů a skupinových axiomů. ${\ displaystyle \ sigma _ {1}}$${\ displaystyle \ sigma _ {2}}$${\ displaystyle \ sigma _ {3}}$

Zobecněním tohoto příkladu na prameny lze skupinu abstraktně definovat pomocí následující prezentace : ${\ displaystyle n}$${\ displaystyle B_ {n}}$

${\ displaystyle B_ {n} = \ left \ langle \ sigma _ {1}, \ ldots, \ sigma _ {n-1} \ mid \ sigma _ {i} \ sigma _ {i + 1} \ sigma _ { i} = \ sigma _ {i + 1} \ sigma _ {i} \ sigma _ {i + 1}, \ sigma _ {i} \ sigma _ {j} = \ sigma _ {j} \ sigma _ {i } \ doprava \ rangle,}$

kde v první skupině vztahů a ve druhé skupině vztahů . Tato prezentace vede k zevšeobecnění skupin copánků, které se nazývají skupiny Artin . Kubické vztahy, známé jako opletení , hrají důležitou roli v teorii Yang-Baxterových rovnic . ${\ displaystyle 1 \ leq i \ leq n-2}$${\ displaystyle ij \ geq 2}$

Další vlastnosti

• Skupina opletení je triviální , je nekonečná cyklická skupina , a je izomorfní k uzlu skupiny v trojlístku uzlu - zejména se jedná o nekonečný non-abelian skupina . ${\ displaystyle B_ {1}}$${\ displaystyle B_ {2}}$ ${\ displaystyle \ mathbb {Z}}$${\ displaystyle B_ {3}}$
• Skupina opletení n- pramenů se vloží jako podskupina do skupiny opletení opletením přidáním dalšího vlákna, které nepřekročí žádné z prvních n řetězců. Rostoucí spojení skupin copánků se všemi je nekonečná skupina copánků . ${\ displaystyle B_ {n}}$${\ displaystyle (n + 1)}$${\ displaystyle B_ {n + 1}}$${\ displaystyle n \ geq 1}$ ${\ displaystyle B _ {\ infty}}$
• Všechny prvky jiné než identity mají nekonečné pořadí ; tj. je bez kroucení . ${\ displaystyle B_ {n}}$${\ displaystyle B_ {n}}$
• K dispozici je levý invariantní lineární uspořádání na nazývá pořadí Dehornoy . ${\ displaystyle B_ {n}}$
• For , obsahuje podskupinu isomorfní s volnou skupinou na dvou generátorech. ${\ displaystyle n \ geq 3}$${\ displaystyle B_ {n}}$
• Existuje homomorfismus definovaný σ _i ↦ 1 . Například opletení σ ₂ σ ₃ σ ₁ ⁻¹ σ ₂ σ ₃ je namapováno na 1 + 1 - 1 + 1 + 1 = 3 . Tato mapa odpovídá abelianizaci skupiny opletení. Protože σ _i ^k ↦ k , pak σ _i ^k je identita právě tehdy . To dokazuje, že generátory mají nekonečný řád. ${\ displaystyle B_ {n} \ to \ mathbb {Z}}$${\ displaystyle k = 0}$

Interakce

Vztah se symetrickou skupinou a skupinou čistého copu

Zapomenutím na to, jak se prameny krouží a kříží, každý oplet na n pramenech určuje permutaci na n prvcích. Toto přiřazení je do a kompatibilní s kompozicí, a proto se stává surjektivní grupou homomorfismu B _n → S _n ze skupiny copu do symetrické skupiny . Obraz opletení σ _i ∈ B _n je transpozice s _i = ( i , i +1) ∈ S _n . Tyto transpozice generují symetrickou skupinu, uspokojují vztahy skupiny opletení a mají pořadí 2. To transformuje Artinovu prezentaci skupiny opletení na Coxeterovu prezentaci symetrické skupiny:

${\ displaystyle S_ {n} = \ left \ langle s_ {1}, \ ldots, s_ {n-1} | s_ {i} s_ {i + 1} s_ {i} = s_ {i + 1} s_ { i} s_ {i + 1}, s_ {i} s_ {j} = s_ {j} s_ {i} {\ text {pro}} | ij | \ geq 2, s_ {i} ^ {2} = 1 \ right \ rangle.}$

Jádro z homomorfismu B _n → S _n je podskupina B _n nazývá čistý cop skupinou n pramenů a označený P _n . V čistém copu jsou začátek a konec každého vlákna ve stejné poloze. Skupiny čistých copů zapadají do krátké přesné sekvence

${\ displaystyle 1 \ až F_ {n-1} \ až P_ {n} \ až P_ {n-1} \ až 1.}$

Tato sekvence se rozdělí, a proto se čisté skupiny opletení realizují jako iterované polopřímé produkty volných skupin.

Vztah mezi a modulární skupinou ${\ displaystyle B_ {3}}$

Skupina opletení je univerzální centrální rozšíření o modulární skupiny , s těmito sedí jako latexy uvnitř (topologické) univerzální krycí skupiny ${\ displaystyle B_ {3}}$ ${\ displaystyle \ mathrm {PSL} (2, \ mathbb {Z})}$

${\ displaystyle {\ overline {\ mathrm {SL} (2, \ mathbb {R})}} \ to \ mathrm {PSL} (2, \ mathbb {R})}$ .

Kromě toho je modulární skupina triviální centrum, a tím i modulární skupina je isomorphic k kvocientu skupiny z modulo jeho středu , a ekvivalentně do skupiny vnitřních automorphisms z . ${\ displaystyle B_ {3}}$${\ displaystyle Z (B_ {3}),}$${\ displaystyle B_ {3}}$

Zde je konstrukce tohoto izomorfismu . Definovat

${\ displaystyle a = \ sigma _ {1} \ sigma _ {2} \ sigma _ {1}, \ quad b = \ sigma _ {1} \ sigma _ {2}}$ .

Ze vztahů opletení to vyplývá . Označíme-li tento druhý produkt jako , lze si z copánkových vztahů ověřit, že ${\ displaystyle a ^ {2} = b ^ {3}}$${\ displaystyle c}$

${\ displaystyle \ sigma _ {1} c \ sigma _ {1} ^ {- 1} = \ sigma _ {2} c \ sigma _ {2} ^ {- 1} = c}$

z čehož vyplývá, že je ve středu . Nechť značí podskupinu z generované pomocí C , protože C  ⊂  Z ( B ₃ ) , to je normální podskupina a jeden může mít podíl skupiny B ₃ / C . Nárokujeme B ₃ / C ≅ PSL (2, Z ) ; tento izomorfismus může mít explicitní formu. Tyto cosets å ₁ ° C a å ₂ C mapy že ${\ displaystyle c}$${\ displaystyle B_ {3}}$${\ displaystyle C}$${\ displaystyle B_ {3}}$

${\ displaystyle \ sigma _ {1} C \ mapsto R = {\ začátek {bmatrix} 1 & 1 \\ 0 a 1 \ konec {bmatrix}} \ qquad \ sigma _ {2} C \ mapsto L ^ {- 1} = {\ začátek {bmatrix} 1 a 0 \\ - 1 a 1 \ konec {bmatrix}}}$

kde L a R jsou standardní levé a pravé pohyby na stromě Stern – Brocot ; je dobře známo, že tyto pohyby generují modulární skupinu.

Alternativně je jedna společná prezentace pro modulární skupinu

${\ displaystyle \ langle v, p \, | \, v ^ {2} = p ^ {3} = 1 \ rangle}$

kde

${\ displaystyle v = {\ begin {bmatrix} 0 & 1 \\ - 1 & 0 \ end {bmatrix}}, \ qquad p = {\ begin {bmatrix} 0 & 1 \\ - 1 & 1 \ end {bmatrix}}.}$

Mapování a na v a b na p poskytne surjektivní skupinový homomorfismus B ₃ → PSL (2, Z ) .

Střed B ₃ se rovná C , v důsledku těchto skutečností: c je v centru, modulární skupina triviální centrum, a výše surjective homomorfismu má jádro C .

Vztah ke skupině tříd mapování a klasifikace copánků

Opletení skupina B _n může být prokázáno, že isomorphic k mapování třídy skupiny části proraženou kotouče s n propíchnutí. To je nejjednodušší vizualizovat představováním každé propíchnutí, které je spojeno řetězcem s hranicí disku; každý homomorfismus mapování, který permutuje dvě z propíchnutí, lze poté považovat za homotopii řetězců, tj. opletení těchto řetězců.

Pomocí této interpretace skupinových mapování tříd prýmků lze každý prýmek klasifikovat jako periodický, redukovatelný nebo pseudo-Anosov .

Spojení s teorií uzlů

Pokud je uveden opletení a jeden spojuje první levou položku s první pravou položkou pomocí nového řetězce, druhá levá položka s druhou pravou položkou atd. (Bez vytváření jakýchkoli copánků v nových řetězcích ), jeden získá odkaz a někdy i uzel . Alexanderova věta v teorii opletení uvádí, že platí i obrácení : každý uzel a každý odkaz vznikají tímto způsobem z alespoň jednoho opletení; takový cop lze získat odříznutím článku. Vzhledem k tomu, že prýmky lze v generátorech σ _i konkrétně zadat jako slova , je to často preferovaná metoda zadávání uzlů do počítačových programů.

Výpočtové aspekty

Slovní úloha pro opletu vztahy je efektivně řešitelný a existuje normální forma pro prvky B, _n , pokud jde o generátory å ₁ , ..., å _{n -1} . ( Výpočet normální formy opletení je v podstatě algebraickým analogem „tažení pramenů“, jak je znázorněno v naší druhé sadě obrázků výše.) Počítačový algebraický systém GAP zdarma může provádět výpočty v B _n, pokud jsou dané prvky z hlediska těchto generátorů. K dispozici je také balíček s názvem CHEVIE pro GAP3 se speciální podporou skupin copánků. Slovní úloha je také efektivně řešena prostřednictvím reprezentace Lawrence – Krammer .

Kromě slovního problému existuje několik známých náročných výpočetních problémů, které by mohly implementovat skupiny copánků , bylo navrženo použití v kryptografii .

Akce

Analogicky s působením symetrické skupiny permutacemi existuje v různých matematických nastaveních přirozené působení skupiny opletení na n -tuple objektů nebo na n- složený tenzorový produkt, který zahrnuje některé „zvraty“. Uvažujme libovolnou skupinu G a nechat X je množina všech n -tuples prvků ze G , jehož produkt je element identity z G . Pak B _n působí na X následujícím způsobem:

${\ displaystyle \ sigma _ {i} \ left (x_ {1}, \ ldots, x_ {i-1}, x_ {i}, x_ {i + 1}, \ ldots, x_ {n} \ right) = \ left (x_ {1}, \ ldots, x_ {i-1}, x_ {i + 1}, x_ {i + 1} ^ {- 1} x_ {i} x_ {i + 1}, x_ {i +2}, \ ldots, x_ {n} \ right).}$

Prvky x _i a x _{i +1 si tedy} vyměňují místa a navíc je x _i zkrouceno vnitřním automorfismem odpovídajícím x _{i +1} - to zajišťuje, že produkt komponent x zůstává identitním prvkem. Může být zkontrolováno, že prýmek skupina vztahy jsou splněny a tento vzorec skutečně definuje akce skupin B, _n na X . Jako další příklad, je spletené monoidal kategorie je monoidal kategorie s působením copu skupiny. Takové struktury hrají důležitou roli v moderní matematické fyzice a vedou k invariantům kvantových uzlů .

Zastoupení

Prvky skupiny opletení B _n lze konkrétněji reprezentovat maticemi. Jedna klasická taková reprezentace je Burauova reprezentace , kde položky matice jsou jednotlivé proměnné Laurentovy polynomy . Byla to dlouholetá otázka, zda je zastoupení Burau věrné , ale odpověď se pro n  ≥ 5 ukázala být negativní . Obecněji řečeno, bylo velkým otevřeným problémem, zda byly skupiny opletení lineární . V roce 1990 popsala Ruth Lawrence rodinu obecnějších „Lawrencových reprezentací“ v závislosti na několika parametrech. V roce 1996 Chetan Nayak a Frank Wilczek tvrdili, že analogicky k projektivním reprezentacím SO (3) mají projektivní reprezentace skupiny copů fyzický význam pro určité kvazičástice ve frakčním kvantovém Hallově jevu . Kolem roku 2001 Stephen Bigelow a Daan Krammer nezávisle dokázali, že všechny skupiny opletení jsou lineární. Jejich práce používala Lawrence – Krammerovu reprezentaci dimenze v závislosti na proměnných q a t . Vhodnou specializací těchto proměnných může být skupina opletení realizována jako podskupina obecné lineární skupiny přes komplexní čísla . ${\ displaystyle n (n-1) / 2}$${\ displaystyle B_ {n}}$

Nekonečně generované skupiny opletení

Existuje mnoho způsobů, jak tuto představu zobecnit na nekonečné množství pramenů. Nejjednodušším způsobem je použít přímý limit skupin copánků, kde připojující mapy posílají generátory prvních generátorů (tj. Připojením triviálního řetězce). Paul Fabel ukázal, že existují dvě topologie, které lze uvalit na výslednou skupinu, přičemž každá z jejich dokončení přináší jinou skupinu. Jeden je velmi krotká skupina a je izomorfní ke skupině tříd mapování nekonečně propíchnutého disku - diskrétní sada propíchnutí omezující na hranici disku . ${\ displaystyle f \ tračník B_ {n} \ až B_ {n + 1}}$${\ displaystyle n-1}$${\ displaystyle B_ {n}}$${\ displaystyle n-1}$${\ displaystyle B_ {n + 1}}$

Druhá skupina může být považována za stejnou jako u skupin konečných copů. Umístěte vlákno do každého z bodů a sada všech copánků - kde je cop definovaný jako soubor cest od bodů k bodům, takže funkce poskytuje permutaci v koncových bodech - je pro tuto divokější skupinu izomorfní. Zajímavé je, že čistý opletení skupina v této skupině je izomorfní jak pro inverzní limitu konečných čistých opletení skupin a do základní skupiny v Hilbertovy krychle minus sadě ${\ displaystyle (0,1 / n)}$${\ displaystyle (0,1 / n, 0)}$${\ displaystyle (0,1 / n, 1)}$${\ displaystyle P_ {n}}$

${\ displaystyle \ {(x_ {i}) _ {i \ in \ mathbb {N}} \ střední x_ {i} = x_ {j} {\ text {pro některé}} i \ neq j \}.}$

Kohomologie

Kohomologie skupiny je definován jako kohomologie odpovídající Eilenberg-MacLane třídicím prostoru , , který je CW komplex jednoznačně určen až do homotopy. Třídícího prostoru pro skupinu opletení je n ^th neuspořádané prostoru konfigurace části , která je, množina různých neuspořádané bodů v rovině: ${\ displaystyle G}$ ${\ displaystyle K (G, 1)}$${\ displaystyle G}$${\ displaystyle B_ {n}}$${\ displaystyle \ mathbb {R} ^ {2}}$${\ displaystyle n}$

${\ displaystyle \ operatorname {UConf} _ {n} (\ mathbb {R} ^ {2}) = \ {\ {u_ {1}, ..., u_ {n} \}: u_ {i} \ in \ mathbb {R} ^ {2}, u_ {i} \ neq u_ {j} {\ text {for}} i \ neq j \}}$ .

Takže podle definice

${\ displaystyle H ^ {*} (B_ {n}) = H ^ {*} (K (B_ {n}, 1)) = H ^ {*} (\ operatorname {UConf} _ {n} (\ mathbb {R} ^ {2})).}$

Výpočty koeficientů v lze nalézt v Fuks (1970). ${\ displaystyle \ mathbb {Z} / 2 \ mathbb {Z}}$

Podobně třídicí prostor pro čistou opletení skupiny je se n ^th objednat konfigurace prostor o . V roce 1968 Vladimir Arnold ukázal, že integrální kohomologie skupiny čistých copů je kvocientem vnější algebry generované sbírkou tříd prvního stupně , s výhradou vztahů ${\ displaystyle P_ {n}}$${\ displaystyle \ operatorname {Conf} _ {n} (\ mathbb {R} ^ {2})}$ ${\ displaystyle \ mathbb {R} ^ {2}}$${\ displaystyle P_ {n}}$${\ displaystyle \ omega _ {ij} \; \; 1 \ leq i <j \ leq n}$

${\ displaystyle \ omega _ {k, \ ell} \ omega _ {\ ell, m} + \ omega _ {\ ell, m} \ omega _ {m, k} + \ omega _ {m, k} \ omega _ {k, \ ell} = 0.}$

Viz také

• Artin – prsa skupina
• Pletená monoidní kategorie
• Opletené vektorový prostor
• Pletená Hopfova algebra
• Změna softwaru pro vyzvánění - jak software používá teorii opletení k modelování vzorů zvonění
• Teorie uzlů
• Nekomutativní kryptografie

Reference

Další čtení

externí odkazy

• "Braid group" . PlanetMath .
• CRAG: CRyptography and Groups at Algebraic Cryptography Center Obsahuje rozsáhlou knihovnu pro výpočty s Braid Groups
• [1] Teorie vizuálních skupin, přednáška 1.3: Skupiny ve vědě, umění a matematice
• Fabel, Paul (2005), „Dokončení Artinovy ​​skupiny copu na nekonečně mnoha pramenech“, Journal of Knot Theory and Its Ramifications , 14 (8): 979–991, arXiv : math / 0201303 , doi : 10,1142 / S0218216505004196 , MR   2196643
• Fabel, Paul (2006), „Skupina tříd mapování disku s nekonečně mnoha otvory“, Journal of Knot Theory and Its Ramifications , 15 (1): 21–29, arXiv : math / 0303042 , doi : 10,1142 / S0218216506004324 , MR   2204494
• Chernavskii, AV (2001) [1994], „Braid theory“ , Encyclopedia of Mathematics , EMS Press
• Bigelow, Stephene . "Průzkum appletu B5 Java" .
• Nayak, Chetan; Wilczek, Frank (1996), „$ 2n $ Quasihole States Realize $ 2 ^ {n-1} $ - Dimensional Spinor Braiding Statistics in Paired Quantum Hall States“, Nuclear Physics B , 479 (3): 529–553, arXiv : cond -mat / 9605145 , Bibcode : 1996NuPhB.479..529N , doi : 10.1016 / 0550-3213 (96) 00430-0 - připojení reprezentací projektivní skupiny copů k frakčnímu kvantovému Hallovu jevu
• Prezentace na FradkinFest od Chetana V. Nayaka [2]
• Read, N. (2003), „Nonabelian braid statistics versus projectective permutation statistics“, Journal of Mathematical Physics , 44 (2): 558–563, arXiv : hep-th / 0201240 , Bibcode : 2003JMP .... 44 .. 558R , doi : 10,1063 / 1,1530369 - kritika reality zastoupení Wilczek-Nayak
• Stránka Lipmaa, Helger, Cryptography and Braid Groups , archivovaná od originálu dne 3. srpna 2009
• Skupina Braid: Seznam autoritních článků na arxiv.org .
• "Braids - film" Film v počítačové grafice, který vysvětluje některé teorie copánků (skupinová prezentace, slovní úloha, uzavřené copánky a odkazy, copánky jako pohyby bodů v rovině).
• VÍTĚZ časopisu Science 2017 Dance Dance PhD: Zastoupení skupin Braid . Nancy Scherich.
• Behind the Math of Dance Your PhD, Part 1: The Braid Groups. Nancy Scherich. Vysvětlení skupin copánků použitých ve filmu.