Konvexní sada - Convex set

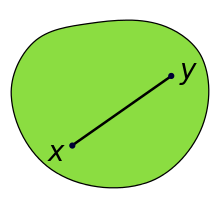
Ilustrace konvexní sady, která vypadá poněkud jako deformovaný kruh. Segment čáry, znázorněný černě výše, spojující body x a y, leží zcela uvnitř sady, znázorněný zeleně. Protože to platí pro všechna potenciální umístění jakýchkoli dvou bodů v rámci výše uvedené sady, je sada konvexní.

Ilustrace nekonvexní sady. Ilustruje výše uvedený segment čáry, přičemž se mění z černé na červenou. Vysvětlující, proč tato sada, znázorněná zeleně, není konvexní.

V geometrii je podmnožina euklidovského prostoru , nebo obecněji afinního prostoru nad reálnými oblastmi , konvexní, pokud vzhledem k jakýmkoli dvěma bodům v podmnožině obsahuje podmnožina celý segment čáry, který je spojuje. Ekvivalentně je konvexní množina nebo konvexní oblast podmnožinou, která protíná každý řádek do jednoho segmentu řádku (případně prázdného). Například plná krychle je konvexní množina, ale vše, co je duté nebo má odrážku, například tvar půlměsíce , není konvexní.

Hranice konvexní sady je vždy konvexní křivku . Průsečík všech konvexních množin, které obsahují daný podmnožinu $A$ v euklidovském prostoru se nazývá konvexní trup z $A$ . Je to nejmenší konvexní množina obsahující $A$ .

Konvexní funkce je reálná funkce definované na intervalu se vlastnost, že jeho epigraf (množina bodů na nebo nad grafem funkce) je konvexní množina. Konvexní minimalizace je podoblast optimalizace, která studuje problém minimalizace konvexních funkcí nad konvexními množinami. Obor matematiky věnovaný studiu vlastností konvexních množin a konvexních funkcí se nazývá konvexní analýza .

Pojem konvexní množiny lze zobecnit, jak je popsáno níže.

Definice

Funkce je konvexní, jestliže a pouze tehdy, když jeho epigraf , oblast (zeleně) nad jeho grafu (modře), je konvexní množina.

Nechť $S$ je vektorový prostor nebo afinní prostor nad skutečnými čísly , nebo obecněji nad nějakým uspořádaným polem . To zahrnuje euklidovské prostory, což jsou afinní prostory. Podmnožina $C$ z $S$ je konvexní , jestliže pro všechny $x$ a $y$ v $C$ je úsečka spojující $x$ a $y$ je součástí $C$ . To znamená, že afinní kombinace $(1 - t), x + ty$ patří do $C$ , pro všechny $x$ a $y$ v $C$ , a $t$ v intervalu $[0, 1]$ . To znamená, že konvexita (vlastnost být konvexní) je při afinních transformacích neměnná . To také znamená, že konvexní množina ve skutečném nebo komplexním topologickém vektorovém prostoru je spojena s cestou , tedy spojena .

Sada $C$ je striktně konvexní jestliže každý bod úsečky spojující $X$ a $Y$ jiné než v koncových bodech je uvnitřvnitřního prostoruo $C$ .

Sada $C$ je absolutně konvexní, pokud je konvexní a vyvážená .

Konvexní podmnožiny z $R$ (soubor reálných čísel) jsou intervaly a body $R$ . Některé příklady konvexních podmnožin euklidovské roviny jsou pevné pravidelné polygony , plné trojúhelníky a průsečíky plných trojúhelníků. Některé příklady konvexních podmnožin euklidovského 3-dimenzionálního prostoru jsou archimédské tělesa a platonické tělesa . Tyto Kepler-Poinsot mnohostěn jsou příklady non-konvexní množiny.

Nekonvexní sada

Množina, která není konvexní, se nazývá nekonvexní . Polygon , který není konvexní polygon je někdy nazýván konkávní polygon , a některé zdroje obecně používat termín sadu konkávní znamenat non-konvexní množina, ale většina úřadů zakázat toto použití.

Doplněk konvexní množiny, jako je epigrafu části konkávní funkce , je někdy nazýván reverzní sadu konvexní , a to zejména v souvislosti s matematické optimalizace .

Vlastnosti

Je -li $r$ bodů $u 1, ..., u r$ v konvexní množině $S$ , a $r$ nezáporných čísel $λ 1, ..., λ r$ tak, že $λ 1 + ... + λ r = 1$ , afinní kombinace

{\ Displaystyle \ sum _ {k = 1}^{r} \ lambda _ {k} u_ {k}}

patří

S

. Protože definice konvexní sady je případ

r = 2

, tato vlastnost charakterizuje konvexní sady.

Takový afinní kombinace se nazývá konvexní kombinace o $u 1, ..., u r$ .

Křižovatky a svazy

Kolekce konvexních podmnožin vektorového prostoru, afinního prostoru nebo euklidovského prostoru má následující vlastnosti:

Prázdná množina a celý prostor jsou konvexní.
Průnik jakékoli kolekce konvexních sad je konvexní.
Unie sekvence konvexních množin je konvexní, v případě, že tvoří neklesající řetězce pro začlenění. Pro tuto vlastnost je důležité omezení řetězců, protože spojení dvou konvexních sad nemusí být konvexní.

Uzavřené konvexní sady

Uzavřené konvexní sady jsou konvexní sady, které obsahují všechny své mezní body . Mohou být charakterizovány jako průsečíky uzavřených poloprostorů (množiny bodů v prostoru, které leží na jedné straně a na jedné straně nadroviny ).

Z toho, co bylo právě řečeno, je zřejmé, že takové křižovatky jsou konvexní a budou to také uzavřené množiny. K prokázání opaku, tj. Každá uzavřená konvexní množina může být reprezentována jako taková křižovatka, je zapotřebí podpůrná věta o hyperplane ve formě, že pro danou uzavřenou konvexní množinu $C$ a bod $P$ mimo ni existuje uzavřený půlprostor $H,$ který obsahuje $C$ a ne $P$ . Podpůrná věta o hyperplane je zvláštním případem Hahnovy -Banachovy věty o funkční analýze .

Konvexní sady a obdélníky

Nechť $C$ je konvexní těleso v rovině (konvexní množina, jejíž vnitřek není prázdný). Můžeme vepsat obdélník r do $C$ tak, že kolem $C$ je ohraničena homotetická kopie R z r . Pozitivní poměr homothety je maximálně 2 a:

{\ Displaystyle {\ tfrac {1} {2}} \ cdot \ operatorname {Area} (R) \ leq \ operatorname {Area} (C) \ leq 2 \ cdot \ operatorname {Area} (r)}

Blaschke-Santalóovy diagramy

Soubor všech rovinných konvexních těles lze parametrizovat, pokud jde o konvexní těleso průměr D , její inradius R (největší kruh obsažený v klenutého těla) a jeho circumradius R (nejmenší kruh obsahující konvexní těleso). Ve skutečnosti lze tuto množinu popsat množinou nerovností danou ${\ displaystyle {\ mathcal {K}}^{2}}$

{\ Displaystyle 2r \ leq D \ leq 2R}

{\ Displaystyle R \ leq {\ frac {\ sqrt {3}} {3}} D}

{\ displaystyle r+R \ leq D}

{\ Displaystyle D^{2} {\ sqrt {4R^{2} -D^{2}}} \ leq 2R (2R+{\ sqrt {4R^{2} -D^{2}}})}}

a lze jej zobrazit jako obraz funkce g, která mapuje konvexní těleso na bod

R 2

daný vztahem ( r / R , D / 2 R ). Obraz této funkce je znám jako ( r , D , R ) Blachke-Santalóův diagram.

Blaschke-Santaló ( r , D , R ) diagram pro rovinná konvexní tělesa. označuje segment čáry, je rovnostranný trojúhelník, na Reuleauxe trojúhelník a kruh jednotky.

{\ displaystyle \ mathbb {L}}

{\ displaystyle \ mathbb {I} _ {\ frac {\ pi} {3}}}

{\ displaystyle \ mathbb {RT}}

{\ displaystyle \ mathbb {B} _ {2}}

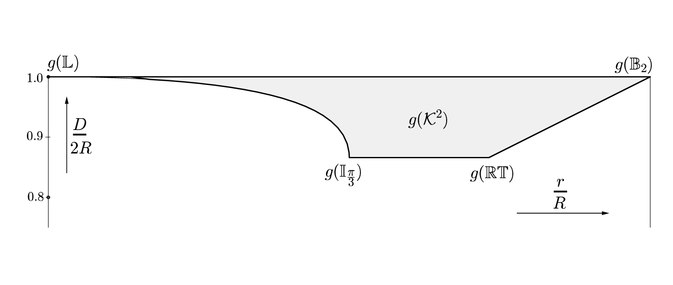
Alternativně lze sadu také parametrizovat její šířkou (nejmenší vzdálenost mezi libovolnými dvěma různými rovnoběžnými podpěrnými rovinami), obvodem a plochou. ${\ displaystyle {\ mathcal {K}}^{2}}$

Další vlastnosti

Nechť X je topologický vektorový prostor a je konvexní. ${\ displaystyle C \ subseteq X}$

${\ displaystyle \ operatorname {Cl} C}$ a jsou oba konvexní (tj. uzavření a vnitřek konvexních sad jsou konvexní). ${\ displaystyle \ operatorname {Int} C}$
Pokud a pak (kde ). ${\ displaystyle a \ in \ operatorname {Int} C}$ ${\ displaystyle b \ in \ operatorname {Cl} C}$ ${\ displaystyle [a, b [\, \ subseteq \ operatorname {Int} C}$ ${\ Displaystyle [a, b [\,: = \ left \ {(1-r) a+rb: 0 \ leq r <1 \ right \}}$
Pokud pak: ${\ displaystyle \ operatorname {Int} C \ neq \ emptyset}$ ${\ displaystyle \ operatorname {Int} C \ neq \ emptyset}$
- ${\ displaystyle \ operatorname {cl} \ left (\ operatorname {Int} C \ right) = \ operatorname {Cl} C}$ , a
- ${\ displaystyle \ operatorname {Int} C = \ operatorname {Int} \ left (\ operatorname {Cl} C \ right) = C^{i}}$ , Kde je algebraická vnitřek z C . ${\ displaystyle C^{i}}$

Konvexní trupy a Minkowského součty

Konvexní trupy

Každá podmnožina vektorového prostoru je obsažena v nejmenší konvexní množina (nazývá se konvexní obal z $A$ ), a to v průsečíku všech konvexních množin, které obsahují $A$ . Operátor konvexního trupu Conv () má charakteristické vlastnosti jako operátor trupu :

rozsáhlé : $S \subseteq Conv (S)$ ,
neklesající : $S \subseteq T$ znamená, že $Conv (S) \subseteq Conv (T)$ , a
idempotent : $Conv (Conv (S)) = Conv (S)$ .

Operace konvexního trupu je potřebná k tomu, aby sada konvexních sad vytvořila mříž , ve které je operace „ spojení “ konvexním trupem spojení dvou konvexních sad

{\ displaystyle \ operatorname {Conv} (S) \ vee \ operatorname {Conv} (T) = \ operatorname {Conv} (S \ cup T) = \ operatorname {Conv} {\ bigl (} \ operatorname {Conv} ( S) \ cup \ operatorname {Conv} (T) {\ bigr)}.}

Průsečík jakékoli kolekce konvexních množin je sám konvexní, takže konvexní podmnožiny (skutečného nebo komplexního) vektorového prostoru tvoří úplnou mřížku .

Doplnění Minkowski

Minkowski přidání sad. Součet čtverců Q ₁ = [0,1] ² a Q ₂ = [1,2] ² je čtvercový Q ₁ + Q ₂ = [1,3] ² .

Ve skutečném vektorovém prostoru je Minkowského součet dvou (neprázdných) množin, $S 1$ a $S 2$ , definován jako množina $S 1 + S 2$ vytvořená přidáním vektorů po elementech ze součtových sad

{\ Displaystyle S_ {1}+S_ {2} = \ {x_ {1}+x_ {2}: x_ {1} \ v S_ {1}, x_ {2} \ v S_ {2} \}.}

Obecněji řečeno, Minkowského součet konečné rodiny (neprázdných) množin

S n

je množina tvořená elementárním sčítáním vektorů

{\ Displaystyle \ sum _ {n} S_ {n} = \ left \ {\ sum _ {n} x_ {n}: x_ {n} \ in S_ {n} \ right \}.}

Pro Minkowského sčítání má zvláštní význam nulová množina ${0}$ obsahující pouze nulový vektor $0$ : Pro každou neprázdnou podmnožinu S vektorového prostoru

{\ Displaystyle S+\ {0 \} = S;}

v algebraické terminologii,

{0}

je element identity z Minkovského kromě (na sběr neprázdné sady).

Konvexní trupy součtů Minkowski

Minkowského adice se chová dobře, pokud jde o operaci odebírání konvexních slupek, jak ukazuje následující tvrzení:

Nechť $S 1, S 2$ jsou podmnožinami skutečného vektorového prostoru, konvexní trup jejich Minkowského součtu je Minkowského součet jejich konvexních trupů

{\ displaystyle \ operatorname {Conv} (S_ {1}+S_ {2}) = \ operatorname {Conv} (S_ {1})+\ operatorname {Conv} (S_ {2}).}

Tento výsledek platí obecněji pro každou konečnou kolekci neprázdných sad:

{\ displaystyle {\ text {Conv}} \ left (\ sum _ {n} S_ {n} \ right) = \ sum _ {n} {\ text {Conv}} \ left (S_ {n} \ right) .}

V matematické terminologie, se operace z Minkovského shrnutí a formování konvexní trupy jsou dojíždění operace.

Minkowského součty konvexních sad

Minkowského součet dvou kompaktních konvexních sad je kompaktní. Součet kompaktní konvexní sady a uzavřené konvexní sady je uzavřen.

Následující slavná věta, kterou Dieudonné dokázala v roce 1966, dává dostatečnou podmínku k uzavření rozdílu dvou uzavřených konvexních podmnožin. Používá koncept recesního kužele neprázdné konvexní podmnožiny S , definovaný jako:

{\ displaystyle \ operatorname {rec} S = \ left \ {x \ in X \,: \, x+S \ subseteq S \ right \},}

kde tato sada je konvexní kužel obsahující a uspokojující . Všimněte si, že pokud je S uzavřené a konvexní, pak je uzavřeno a pro všechny ,

{\ displaystyle 0 \ v X}

{\ displaystyle S+\ operatorname {rec} S = S}

{\ displaystyle \ operatorname {rec} S}

{\ displaystyle s_ {0} \ in S}

{\ displaystyle \ operatorname {rec} S = \ bigcap _ {t> 0} t (S-s_ {0}).}

Věta (Dieudonné). Nechť A a B jsou neprázdné, uzavřené a konvexní podmnožiny místně konvexního topologického vektorového prostoru , což je lineární podprostor. Pokud nebo

B je lokálně kompaktní tehdy - B je uzavřen.

{\ displaystyle \ operatorname {rec} A \ cap \ operatorname {rec} B}

Zobecnění a rozšíření pro konvexitu

Pojem konvexity v euklidovském prostoru lze zobecnit úpravou definice v některých nebo jiných aspektech. Používá se běžný název „generalizovaná konvexita“, protože výsledné objekty si zachovávají určité vlastnosti konvexních množin.

Hvězdně konvexní (hvězdicovité) sady

Nechť $C$ je množina ve skutečném nebo komplexním vektorovém prostoru. $C$ je hvězda konvexní (hvězdicovité) , když existuje $x 0$ v $C,$ tak, aby úsečka od $x 0$ do jakéhokoli místa $y$ v $C$ je obsažen v $C$ . Proto je neprázdná konvexní sada vždy konvexní hvězda, ale konvexní sada hvězd není vždy konvexní.

Ortogonální konvexita

Příkladem generalizované konvexity je ortogonální konvexita .

Sada $S$ v euklidovském prostoru se nazývá ortogonálně konvexní nebo ortho-konvexní , případně segmentu rovnoběžná s některou z souřadných os spojujících dva body $S$ lží zcela v $S$ . Je snadné dokázat, že průsečík jakékoli kolekce ortokonvexních sad je ortokonvexní. Platí také některé další vlastnosti konvexních sad.

Neeuklidovská geometrie

Definice konvexní sady a konvexního trupu se přirozeně rozšiřuje na geometrie, které nejsou euklidovské, definováním geodeticky konvexní množiny jako takové, která obsahuje geodetiku spojující libovolné dva body v sadě.

Topologie objednávky

Konvexitu lze rozšířit na zcela uspořádanou sadu $X$ vybavenou topologií objednávky .

Nechť $Y \subseteq X$ . Subprostor $Y$ je konvexní množina, pokud pro každou dvojici bodů $a, b$ v $Y$ tak, že $a \leq b$ , interval $[a, b] = {x \in X | \leq$

x ≤ b } je obsažen v

Y

. To znamená, že

Y

je konvexní právě tehdy, když pro všechny

A, B,

v

Y

,

\leq

b

znamená

[

s

,

b

] \subseteq

Y

.

Konvexní množina není spojena obecně: protipříklad je dán podprostorem {1,2,3} v $Z$ , který je konvexní a není spojen.

Konvexní prostory

Pojem konvexity lze zobecnit na jiné objekty, pokud jsou jako axiomy vybrány určité vlastnosti konvexity .

Vzhledem k množině $X$ je konvexita nad $X$ kolekcí $𝒞$ podmnožin $X$ splňujících následující axiomy:

Prázdná množina a $X$ jsou v $𝒞$
Křižovatka jakékoli kolekce od $𝒞$ je v $𝒞$ .
Sjednocení řetězce (s ohledem na vztah inkluze ) prvků $𝒞$ je v $𝒞$ .

Prvky $𝒞$ se nazývají konvexní sady a dvojici $(X, 𝒞)$ se nazývá konvexnost prostor . Pro běžnou konvexitu platí první dva axiomy a třetí je triviální.

Alternativní definici abstraktní konvexity, vhodnější pro diskrétní geometrii , najdete v konvexních geometriích spojených s antimatroidy .

Viz také

Reference

externí odkazy

„Konvexní podmnožina“ . Encyklopedie matematiky . EMS Stiskněte . 2001 [1994].
Přednášky o konvexních sadách , poznámky Nielse Lauritzena, na Aarhuské univerzitě , březen 2010.

Languages

In other projects