16 článků - 16-cell

Pravidelný hexadecachoron (16 článků) (4-ortoplex)
Schlegelův diagram (vrcholy a hrany)
Typ	Konvexní pravidelný 4-polytope 4- orthoplex 4- demicube
Symbol Schläfli	{3,3,4}
Coxeterův diagram
Buňky	16 {3,3}
Tváře	32 {3}
Hrany	24
Vrcholy	8
Vrcholová figura	Octahedron
Petrieho mnohoúhelník	osmiúhelník
Coxeterova skupina	B 4 , [3,3,4], pořadí 384 D 4 , pořadí 192
Dvojí	Tesseract
Vlastnosti	konvexní , izogonální , izotoxický , izohedrální , pravidelný
Jednotný index	12

V geometrii je 16-buňka je pravidelný konvexní 4-mnohostěn (čtyřrozměrný analog platonické pevné látky) se Schläfli symbolem {3,3,4}. Je to jeden ze šesti pravidelných konvexních 4-polytopů, které poprvé popsal švýcarský matematik Ludwig Schläfli v polovině 19. století. To je také nazýváno C ₁₆ , hexadecachoron nebo hexdecahedroid .

Je součástí nekonečné rodiny polytopů, nazývaných cross-polytopes nebo orthoplexes , a je analogický osmistěnu ve třech rozměrech. Je to Coxeterův polytop. Conway jméno je pro cross-mnohostěnu je orthoplex pro orthant složitá . Dvojí polytope je tesseract (4- kostka ), která může být v kombinaci s k vytvoření složené postavu . 16 buněk má 16 buněk, protože tesseract má 16 vrcholů. ${\ displaystyle \ beta _ {4}}$

Geometrie

16-buňka je druhou v pořadí 6 konvexních pravidelných 4-polytopů (v pořadí podle velikosti a složitosti).

Každá z jeho 4 nástupce konvexní pravidelné 4-polytopes může být vytvořena jako konvexní trup části mnohostěnu sloučeniny více 16-buněk: 16-vrcholu tesseract jako sloučenina dvou 16-buněk je 24 vrchol 24-buněk jako A sloučenina tří 16 buněk, 120 vrcholů 600 buněk jako sloučenina patnácti 16 buněk a 600 vrcholů 120 buněk jako sloučenina sedmdesáti pěti 16 buněk.

Pravidelné konvexní 4-polytopy
Skupina symetrie	A 4	B 4		F 4	H 4
název	5článková Hyper- čtyřstěn	16článková Hyper- osmistěn	8článková Hyper kostka	24článková	600 buněk Hyper- icosahedron	120 článků hyper- dodecahedron
Symbol Schläfli	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeterův diagram
Graf
Vrcholy	5	8	16	24	120	600
Hrany	10	24	32	96	720	1200
Tváře	10 trojúhelníků	32 trojúhelníků	24 čtverců	96 trojúhelníků	1200 trojúhelníků	720 pětiúhelníků
Buňky	5 čtyřstěnů	16 čtyřstěnů	8 kostek	24 oktaedrů	600 čtyřstěnů	120 dodecahedra
Dlouhý rádius	1	1	1	1	1	1
Délka hrany	√ 5/√ 2 ≈ 1,581	√ 2 ≈ 1,414	1	1	1/ϕ ≈ 0,618	1/√ 2 ϕ 2 ≈ 0,270
Krátký rádius	1/4	1/2	1/2	√ 2/2 ≈ 0,707	1 - (√ 2/2 √ 3 φ) 2 ≈ 0,936	1 - (1/2 √ 3 φ) 2 ≈ 0,968
Plocha	10 •√ 8/3 ≈ 9 428	32 •√ 3/4 ≈ 13,856	24	96 •√ 3/4 ≈ 41,569	1200 •√ 3/8φ 2 ≈ 99,238	720 •25+10 √ 5/8φ 4 ≈ 621,9
Objem	5 •5 √ 5/24 ≈ 2,329	16 •1/3 ≈ 5,333	8	24 •√ 2/3 ≈ 11,314	600 •1/3 √ 8 φ 3 ≈ 16,693	120 •2 + φ/2 √ 8 φ 3 ≈ 18,118
4-Obsah	√ 5/24• (√ 5/2) 4 ≈ 0,146	2/3 ≈ 0,667	1	2	Krátký, sv/4 ≈ 3,907	Krátký, sv/4 ≈ 4,385

Souřadnice

16-buňka je 4-dimenzionální křížový polytop , což znamená, že jeho vrcholy leží v opačných dvojicích na 4 osách kartézského souřadného systému a (w, x, y, z).

Osm vrcholů je (± 1, 0, 0, 0), (0, ± 1, 0, 0), (0, 0, ± 1, 0), (0, 0, 0, ± 1). Všechny vrcholy jsou spojeny hranami kromě opačných dvojic. Délka hrany je √ 2 .

Souřadnice vrcholů tvoří 6 ortogonálních centrálních čtverců ležících v 6 souřadnicových rovinách. Čtverce v protilehlých rovinách, které nesdílejí osu (např. V rovinách xy a wz ), jsou zcela disjunktní (neprotínají se na žádných vrcholech).

16-buňka představuje ortonormální základ pro výběr 4-dimenzionálního referenčního rámce, protože jeho vrcholy přesně definují čtyři ortogonální osy.

Struktura

Symbol Schläfli ze 16-buňky je {3,3,4}, což ukazuje, že jeho buňky jsou pravidelné tetraedry {3,3} a jeho číslo vrcholu je pravidelný osmistěn {3,4}. V každém vrcholu se setkává 8 čtyřstěnů, 12 trojúhelníků a 6 hran. Jeho okrajová postava je čtverec. Na každém okraji se setkávají 4 čtyřstěny a 4 trojúhelníky.

16 buněk je ohraničeno 16 buňkami , z nichž všechny jsou pravidelné čtyřstěny . Má 32 trojúhelníkových ploch , 24 hran a 8 vrcholů . 24 hran svázalo 6 ortogonálních středových čtverců ležících na velkých kruzích v 6 souřadnicových rovinách (3 páry zcela ortogonálních velkých čtverců). V každém vrcholu se kříží 3 velké čtverce. Šest okrajů se setkává na vrcholu tak, jak se 6 okrajů setkává na vrcholu kanonické oktaedrální pyramidy .

Rotace

3D projekce 16 buněk provádějící jednoduché otáčení

3D projekce 16 buněk provádějící dvojité otáčení

Rotace ve 4-dimenzionálním euklidovském prostoru lze vnímat jako složení dvou 2-dimenzionálních rotací ve zcela ortogonálních rovinách. 16-buňka je jednoduchý rámec, ve kterém lze pozorovat 4-rozměrné rotace, protože každý ze 6 velkých čtverců 16 buněk má další zcela ortogonální velký čtverec (existují 3 páry zcela ortogonálních čtverců). Mnoho rotací 16-buňky lze charakterizovat úhlem otáčení v jedné z jejích velkých čtvercových rovin (např. Rovina xy ) a dalším úhlem otáčení ve zcela ortogonální velké čtvercové rovině ( rovina wz ). Zcela ortogonální velké čtverce mají disjunktní vrcholy: 4 z 8 vrcholů 16 buněk se otáčí v jedné rovině a další 4 se otáčejí nezávisle ve zcela ortogonální rovině.

Ve 2 nebo 3 rozměrech je rotace charakterizována jedinou rovinou rotace; tento druh otáčení probíhající ve 4prostoru se nazývá jednoduchá rotace , ve které se otáčí pouze jedna ze dvou zcela ortogonálních rovin (úhel otočení v druhé rovině je 0). V 16 buňce se jednoduchá rotace v jedné ze 6 ortogonálních rovin pohybuje pouze 4 z 8 vrcholů; ostatní 4 zůstávají pevné. (V jednoduché animaci otáčení výše se pohybuje všech 8 vrcholů, protože rovina otáčení není jednou ze 6 ortogonálních základních rovin.)

Při dvojité rotaci se pohybují obě sady 4 vrcholů, ale nezávisle: úhly otáčení se mohou ve 2 zcela ortogonálních rovinách lišit. Pokud jsou oba úhly shodné, dochází k maximálně symetrické isoklinické rotaci . V 16článkové izoklinické rotaci o 90 stupňů jakékoli dvojice zcela ortogonálních čtvercových rovin přenese každou čtvercovou rovinu do její zcela ortogonální čtvercové roviny.

Stavby

Oktaedrální dipyramid

Octahedron ${\ displaystyle \ beta _ {3}}$	16článková ${\ displaystyle \ beta _ {4}}$
Ortogonální projekce zkosit šestiúhelník hyperplane

Nejjednodušší konstrukce 16 buněk je na trojrozměrném křížovém mnohostěnu, osmistěnu . Oktaedr má 3 kolmé osy a 6 vrcholů ve 3 protilehlých dvojicích (jeho Petrieho mnohoúhelník je šestiúhelník ). Přidejte další dvojici vrcholů na čtvrtou osu kolmou na všechny 3 ostatní osy. Propojte každý nový vrchol se všemi 6 původními vrcholy a přidejte 12 nových hran. To zvedne dvě oktaedrální pyramidy na sdílenou osmistěnovou základnu, která leží v centrální hyperplaně 16 buněk.

Stereografická projekce 6 ortogonálních středových čtverců 16 buněk na jejich velké kruhy. Každý kruh je rozdělen na 4 obloukové hrany v průsečících, kde 3 kruhy kříží kolmo. Všimněte si, že každý kruh má jednu Clifford paralelní kruh, který to dělá ne protínají. Tyto dva kruhy procházejí navzájem jako sousední články v řetězci.

Oktaedr, kterým stavba začíná, má tři kolmé protínající se čtverce (které se v hexagonálních projekcích objevují jako obdélníky). Každý čtverec se protíná s každým dalším čtvercem na dvou protilehlých vrcholech, přičemž dva ze čtverců se kříží v každém vrcholu. Poté se přidají další dva body ve čtvrté dimenzi (nad a pod 3-dimenzionální hyperplane). Tyto nové vrcholy jsou spojeny se všemi osmiúhelníkovými vrcholy a vytvářejí 12 nových hran a tři další čtverce (které se na projekci objevují jako hrany 3 průměrů šestiúhelníku).

Bylo také vytvořeno něco nevídaného. Všimněte si, že každý čtverec se již neprotíná se všemi ostatními čtverci: protíná se se čtyřmi z nich ( tři čtverce se nyní kříží v každém vrcholu), ale každý čtverec má ještě jeden čtverec, se kterým nesdílí žádné vrcholy: je vůbec přímo nesouvisí s tím náměstím. Tyto dvě oddělené kolmé čtverce (existují tři páry) jsou jako opačné hrany čtyřstěnu: kolmé, ale neprotínající se. Leží proti sobě (v jistém smyslu paralelně) a nedotýkají se, ale také procházejí navzájem jako dva kolmé články v řetězci (ale na rozdíl od článků v řetězci mají společný střed). Jsou příkladem paralelních polygonů Clifford a 16-buňka je nejjednodušší pravidelný polytop, ve kterém se vyskytují. Zde se objevuje Cliffordův paralelismus a vyskytuje se ve všech následujících 4-dimenzionálních konvexních pravidelných polytopech, kde na něj lze pohlížet jako na určující vztah mezi disjunktními pravidelnými 4-polytopy a jejich kocentrickými částmi. Může se vyskytovat mezi shodnými (podobnými) polytopy 2 nebo více dimenzí. Například, jak je uvedeno výše, všechny následující konvexní pravidelné 4-polytopy jsou sloučeniny více 16-buněk; těch 16 buněk je Cliffordův paralelní polytop .

Wythoffovy stavby

16-buňka má dvě Wythoffovy konstrukce , pravidelnou formu a střídanou formu, zde zobrazené jako sítě , druhá je reprezentována střídavě dvěma barvami čtyřbokých buněk.

Spirálová konstrukce

Síťová a ortogonální projekce

16článkovou buňku lze sestrojit ze dvou Boerdijkových – Coxeterových šroubovic z osmi řetězových čtyřstěnů, z nichž každá je ohnuta ve čtvrté dimenzi do prstence. Tyto dvě kruhové šroubovice se kolem sebe spirálovitě zasouvají a procházejí skrz sebe a vytvářejí spojení Hopf . 16 trojúhelníkových ploch je možné vidět ve 2D síti v trojúhelníkovém obkladu se 6 trojúhelníky kolem každého vrcholu. Fialové okraje představují Petrieho polygon 16 buněk.

16 buněk lze tedy rozložit na dva podobné kruhové řetězce rozdělené mezi buňkami po osmi čtyřstěnech, dlouhé čtyři okraje. Tento rozklad lze pozorovat na konstrukci duoantiprismů o 16 až 4 buňkách: nebo , Schläfliho symbol {2} ⨂ {2} nebo s {2} s {2}, symetrie 4,2 ⁺ , 4, pořadí 64.

Jako konfigurace

Tato konfigurační matice představuje 16 buněk. Řádky a sloupce odpovídají vrcholům, hranám, plochám a buňkám. Diagonální čísla říkají, kolik z každého prvku se vyskytuje v celé 16-buňce. Nediagonální čísla udávají, kolik prvků sloupce se vyskytuje v prvku řádku nebo v něm.

${\ Displaystyle {\ begin {bmatrix} {\ begin {matrix} 8 & 6 & 12 & 8 \\ 2 & 24 & 4 & 4 \\ 3 & 3 & 32 & 2 \\ 4 & 6 & 4 & 16 \ end {matrix}} \ end {bmatrix}}}$

Teselace

4-dimenzionální euklidovský prostor lze tessellovat pravidelnými 16 buňkami. Říká se tomu 16bunkový plástev a má Schläfliho symbol {3,3,4,3}. 16-buňka má tedy vzepětí 120 °. Každá 16článková buňka má 16 sousedů, se kterými sdílí čtyřstěn, 24 sousedů, s nimiž sdílí pouze okraj, a 72 sousedů, se kterými sdílí pouze jeden bod. V tomto mozaikování se schází dvacet čtyři 16 buněk.

Duální mozaikování, 24článková voština , {3,4,3,3}, je tvořena běžnými 24 buňkami . Spolu s tesseractic voštiny {4,3,3,4} to jsou jen tři pravidelné tessellations z R ⁴ .

Projekce

ortografické projekce

Coxeterovo letadlo	B 4	B 3 / D 4 / A 2	B 2 / D 3
Graf
Symetrie vzepětí	[8]	[6]	[4]
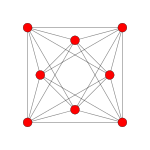
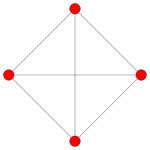
Coxeterovo letadlo	F 4	A 3
Graf
Symetrie vzepětí	[12/3]	[4]

Projekční obálky 16článkové. (Každá buňka je nakreslena různými barvami, obrácené buňky nejsou vykresleny)

Buněčně první paralelní projekce 16 buněk do 3 prostoru má krychlovou obálku. Nejbližší a nejvzdálenější buňky jsou promítnuty na vepsanou čtyřstěnu v krychli, což odpovídá dvěma možným způsobům, jak do kostky vepsat pravidelný čtyřstěn. Každý z těchto čtyřstěnů obklopují 4 další (nepravidelné) čtyřstěnné svazky, které jsou obrazy 4 okolních čtyřstěnných buněk a vyplňují prostor mezi vepsaným čtyřstěnem a krychlí. Zbývajících 6 buněk se promítne na čtvercové plochy krychle. V této projekci 16-buňky leží všechny její hrany na tvářích krychlové obálky.

Perspektivní projekce 16 buněk na první buňku do 3 prostoru má trojúhelníkový trojúhelníkový obal. Rozložení buněk v této obálce je analogické s rovnoběžnou projekcí první buňky.

Vrcholně první paralelní projekce 16 buněk do 3 prostoru má oktaedrickou obálku . Tento osmistěn lze rozdělit na 8 čtyřstěnných svazků řezáním podél souřadnicových rovin. Každý z těchto objemů je obrazem dvojice buněk v 16-buňce. Nejbližší vrchol 16 buněk k divákovi se promítá do středu osmistěnu.

Konečně paralelní projekce na okraji první má zkrácenou oktaedrickou obálku a paralelní projekce na první straně má hexagonální bipyramidovou obálku.

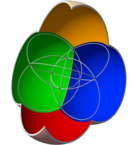
4 sférický Vennův diagram

Trojrozměrná projekce 16 buněk a 4 protínajících se koulí ( Vennův diagram 4 sad) jsou topologicky ekvivalentní.

16 buněk seřazených podle počtu protínajících se koulí (od 0 do 4)     (viz všechny buňky a k -plochy )

4 sférický Vennův diagram a 16buněčná projekce ve stejné orientaci

Symetrické konstrukce

K dispozici je forma nižší symetrie 16 buněk , nazývaná demitesseract nebo 4-demicube , člen rodiny demihypercube , reprezentovaná h {4,3,3}, a Coxeterovými diagramy nebo . Může být nakreslena dvoubarevně se střídajícími se čtyřbokými buňkami.

To může také být viděno ve formě nižší symetrie jako čtyřboký antiprism , konstruovaný 2 paralelními čtyřstěny v duálních konfiguracích, spojených 8 (případně prodlouženými) čtyřstěny. Je reprezentován s {2,4,3} a Coxeterovým diagramem:.

Může být také viděn jako urážlivý 4- ortootop reprezentovaný s {2 ^1,1,1 } a Coxeterovým diagramem: nebo .

S tesseractem zkonstruovaným jako duoprism 4-4 může být 16-buňka vnímána jako duální, duopyramid 4-4 .

název	Coxeterův diagram	Symbol Schläfli	Coxeterova notace	Objednat	Vrcholová figura
Pravidelná 16článková		{3,3,4}	[3,3,4]	384
Quasiregular Demitesseract 16 buněk	= =	h {4,3,3} {3,3 1,1 }	[3 1,1,1 ] = [1 + , 4,3,3]	192
Střídavě 4-4 duoprism		2 s {4,2,4}	[[4,2 + , 4]]	64
Čtyřstěnný antiprism		s {2,4,3}	[2 + , 4,3]	48
Střídaný hranolový hranol		sr {2,2,4}	[(2,2) + , 4]	16
Snub 4- ortootop	=	s {2 1,1,1 }	[2,2,2] + = [2 1,1,1 ] +	8
4- fusil
		{3,3,4}	[3,3,4]	384
		{4}+{4} nebo 2 {4}	[[4,2,4]] = [8,2 + , 8]	128
		{3,4}+{}	[4,3,2]	96
		{4} +2 {}	[4,2,2]	32
		{}+{}+{}+{} nebo 4 {}	[2,2,2]	16

Související komplexní polygony

Möbius-Kantor polygon je pravidelný mnohoúhelník komplex ₃ {3} ₃ ,, ve sdílených částech stejné vrcholy jako 16 buněk. Má 8 vrcholů a 8 3-hran. ${\ displaystyle \ mathbb {C} ^{2}}$

Pravidelný komplexní polygon, ₂ {4} ₄ ,, in má skutečnou reprezentaci jako 16 buněk v 4-dimenzionálním prostoru s 8 vrcholy, 16 2 hran, pouze polovina okrajů 16 buněk. Jeho symetrie je ₄ [4] ₂ , pořadí 32. ${\ displaystyle \ mathbb {C} ^{2}}$

Kolmé projekce z ₂ {4} ₄ polygonu

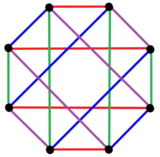V rovině B 4 Coxeter má 2 {4} 4 8 vrcholů a 16 2-hran, zde zobrazených se 4 sadami barev.

8 vrcholů je seskupeno do 2 sad (zobrazeno červeně a modře), z nichž každý je spojen pouze s hranami k vrcholům v druhé sadě, což z tohoto polygonu činí úplný bipartitní graf , K 4,4 .

Související jednotné polytopy a voštiny

Pravidelné 16-buňky spolu s tesseractem existují v sadě 15 stejnoměrných 4-polytopů se stejnou symetrií . Je také součástí jednotných polytopů symetrie D ₄ .

Tento 4-polytope je také příbuzný kubické voštiny , řádu 4 dodekahedrálních plástev a šestihranných obkladových voštin řádu 4, které mají všechny osmihranné vrcholové figury .

To je v pořadí tří běžných 4-Polytopes : ZAŘÍZENÍ 5-buněk {3,3,3}, 600 buněk {3,3,5} Euclidean 4-prostoru, a pořadí-6 čtyřboká plástev {3, 3,6} hyperbolického prostoru. Všechny tyto mají čtyřboké buňky.

Je první v sekvenci kvaziregulárních polytopů a voštin h {4, p, q} a sekvence poloviční symetrie pro pravidelné tvary {p, 3,4}.

Viz také

• 24článková
• 4-mnohostěn
• Polytop D4

Poznámky

Citace

Reference

externí odkazy

• Weisstein, Eric W. „16článková“ . MathWorld .
• Der 16-Zeller (16-cell) Marco Möller's Regular polytopes in R ⁴ (German)
• Popis a diagramy 16článkových projekcí
• Klitzing, Richarde. „4D uniformní polytopy (polychora) x3o3o4o - hex“ .