G ₂ (matematika) -G₂ (mathematics)

Algebraická struktura → Skupinová teorie Skupinová teorie
Základní pojmy Podskupina Normální podskupina Kvocientová skupina (Semi-) přímý produkt Skupinové homomorfismy jádro obraz přímá částka věnec výrobek jednoduchý konečný nekonečný kontinuální multiplikativní přísada cyklický abelian vzepětí nilpotentní řešitelné akce Glosář teorie skupin Seznam témat teorie skupin
Konečné skupiny Klasifikace konečných jednoduchých skupin cyklický střídání Typ lži sporadický Cauchyova věta Lagrangeova věta Sylowovy věty Hallova věta p-skupina Elementární abelianská skupina Skupina Frobenius Schurův multiplikátor Symetrická skupina S n Klein čtyři skupiny V Vzepětí skupina D n Kvaternionová skupina Q Dicyklická skupina Dic n
Diskrétní skupiny Mříže Celá čísla ( )${\ displaystyle \ mathbb {Z}}$ Volná skupina Modulární skupiny PSL (2, )${\ displaystyle \ mathbb {Z}}$ SL (2, )${\ displaystyle \ mathbb {Z}}$ Aritmetická skupina Mříž Hyperbolická skupina
Topologické a Lieovy skupiny Solenoid Kruh Obecné lineární GL ( n ) Speciální lineární SL ( n ) Ortogonální O ( n ) Euklidovský E ( n ) Speciální ortogonální SO ( n ) Unitární U ( n ) Speciální unitární SU ( n ) Symplectic Sp ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Konformní Difeomorfismus Smyčka Nekonečně dimenzionální Lieova skupina O (∞) SU (∞) Sp (∞)
Algebraické skupiny Lineární algebraická skupina Redukční skupina Abelianská odrůda Eliptická křivka
proti t E

Skupiny lži
Klasické skupiny
Jednoduché lživé skupiny Klasický A n B n C n D n Výjimečný G 2 F 4 E 6 E 7 E 8
Jiné skupiny lži Kruh Lorentz Poincaré Konformní skupina Difeomorfismus Smyčka Euklidovský
Lež algebry
Polomatná algebra lži
Teorie reprezentace
Skupiny lži ve fyzice
Vědci Sophus Lie Henri Poincaré Wilhelm zabíjení Élie Cartan Hermann Weyl Claude Chevalley Harish-Chandra Armand Borel
Glosář Tabulka Lieových skupin
proti t E

V matematice je G ₂ název tří jednoduchých Lieových skupin (složitá forma, kompaktní reálná forma a rozdělená reálná forma), jejich Lieových algeber a některých algebraických skupin . Jsou nejmenší z pěti výjimečných jednoduchých Lieových skupin . G ₂ má pozici 2 a dimenzi 14. Má dvě základní reprezentace , s dimenzí 7 a 14. ${\ displaystyle {\ mathfrak {g}} _ {2},}$

Kompaktní forma G _2, může být popsán jako automorphism skupina v oktonion algebry nebo ekvivalentně jako podskupiny tak (7), která zachovává jakékoliv zvolené konkrétní vektor ve své 8-rozměrný reálný spinor znázornění (a znázornění spin ).

Dějiny

Lieova algebra , nejmenší výjimečná jednoduchá Lieova algebra, byla první z nich, která byla objevena při pokusu klasifikovat jednoduché Lieovy algebry. 23. května 1887 Wilhelm Killing napsal dopis Friedrichovi Engelovi , že řekl, že našel 14dimenzionální jednoduchou Lieovu algebru, kterou nyní nazýváme . ${\ displaystyle {\ mathfrak {g}} _ {2}}$${\ displaystyle {\ mathfrak {g}} _ {2}}$

V roce 1893 Élie Cartan publikovala poznámku popisující otevřenou sadu vybavenou 2-dimenzionální distribucí- tj. Plynule se měnící pole 2-dimenzionálních subprostorů tečného prostoru-pro které se Lieova algebra jeví jako nekonečně malé symetrie. Ve stejném roce si Engel ve stejném deníku všiml stejné věci. Později se zjistilo, že dvourozměrné rozdělení úzce souvisí s koulí valící se na jiné kouli. Prostor konfigurací valivé koule je 5-dimenzionální, s 2-dimenzionální distribucí, která popisuje pohyby koule, kde se koule valí, aniž by klouzala nebo se kroutila. ${\ displaystyle \ mathbb {C} ^{5}}$${\ displaystyle {\ mathfrak {g}} _ {2}}$

V roce 1900 Engel zjistil, že generická antisymetrická trilineární forma (nebo 3-forma) na 7-dimenzionálním komplexním vektorovém prostoru je zachována skupinou izomorfní na komplexní formu G ₂ .

V roce 1908 Cartan zmínil, že automorfistická skupina octonionů je 14dimenzionální jednoduchá Lieova skupina. V roce 1914 uvedl, že toto je kompaktní skutečná forma G ₂ .

Ve starších knihách a novinách je G ₂ někdy označován E ₂ .

Skutečné formy

S tímto kořenovým systémem jsou spojeny 3 jednoduché skutečné algebry Lie:

• Základní skutečná Lieova algebra komplexu Lieova algebra G ₂ má rozměr 28. Má komplexní konjugaci jako vnější automorfismus a je jednoduše spojena. Maximální kompaktní podskupina přidružené skupiny je kompaktní forma G ₂ .
• Lieova algebra kompaktní formy je 14-dimenzionální. Přidružená Lieova skupina nemá žádné vnější automorfismy, žádné centrum a je jednoduše propojená a kompaktní.
• Lieova algebra nekompaktní (rozdělené) formy má rozměr 14. Přidružená jednoduchá Lieova skupina má základní skupinu řádu 2 a její vnější skupina automorfismu je triviální skupina. Jeho maximální kompaktní podskupina je SU (2) × SU (2)/( - 1, −1) . Má nealgebraický dvojitý kryt, který je jednoduše spojen.

Algebra

Dynkinův diagram a Cartanova matice

Dynkin diagram pro G ₂ je dána .

Jeho kartanová matice je:

${\ Displaystyle \ left [{\ begin {array} {rr} 2 & -3 \\-1 & 2 \ end {array}} \ right]}$

Kořeny G ₂

12 vektorový kořenový systém G 2 ve 2 rozměrech.

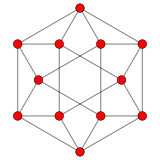Projekce roviny A 2 Coxeteru na 12 vrcholů kvádru obsahuje stejné 2D vektorové uspořádání.

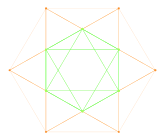Graf G2 jako podskupiny F4 a E8 promítnutý do Coxeterovy roviny

Ačkoli překlenují 2-dimenzionální prostor, jak je nakresleno, je mnohem symetrickější je považovat za vektory ve 2-dimenzionálním subprostoru trojrozměrného prostoru.

(1, −1,0), (−1,1,0) (1,0, −1), (−1,0,1) (0,1, −1), (0, −1,1)

(2, −1, −1), (−2,1,1) (1, −2,1), (−1,2, −1) (1,1, −2), (−1, −1,2)

Jedna sada jednoduchých kořenů , pro je:

(0,1, −1), (1, −2,1)

Weyl/Coxeter skupina

Jeho Weyl / Coxeter skupina je vzepětí skupina , z řádu 12. To má minimální věrný stupeň . ${\ displaystyle G = W (G_ {2})}$${\ displaystyle D_ {6}}$${\ displaystyle \ mu (G) = 5}$

Speciální holonomie

G ₂ je jednou z možných speciálních skupin, které se mohou jevit jako holonomická skupina riemannianské metriky . Tyto variety of G ₂ holonomy jsou také nazývány g ₂ -manifolds .

Polynomiální invariant

G ₂ je skupina automorfismu následujících dvou polynomů v 7 nekomutativních proměnných.

${\ Displaystyle C_ {1} = t^{2}+u^{2}+v^{2}+w^{2}+x^{2}+y^{2}+z^{2}}$

${\ Displaystyle C_ {2} = tuv+wtx+ywu+zyt+vzw+xvy+uxz}$ (± permutace)

který pochází z octonionové algebry. Proměnné musí být nekomutativní, jinak by druhý polynom byl identicky nula.

Generátory

Sečtením reprezentace 14 generátorů s koeficienty A , ...,  N dostaneme matici:

${\ Displaystyle A \ lambda _ {1}+\ cdots+N \ lambda _ {14} = {\ begin {bmatrix} 0 & C & -B & E & -D & -G & F-M \\-C & 0 & A & F & -G+N & D-K & -EL \ \ B & -A & 0 & -N & M & L & -K \\-E & -F & N & 0 & -A+H & -B+I & C-J \\ D & G-N & -M & A-H & 0 & J & I \\ G & K-D & -L & B-I & -J & 0 & -H \\-F +M & E+L & K & -C+J & -I & H & 0 \ end {bmatrix}}}$

Je to přesně Lieova algebra skupiny

${\ Displaystyle G_ {2} = \ {g \ v SO (7): g ^{*} \ varphi = \ varphi, \ varphi = \ omega ^{123}+\ omega ^{145}+\ omega ^{ 167}+\ omega ^{246}-\ omega ^{257}-\ omega ^{347}-\ omega ^{356} \}}$

Zastoupení

Znaky konečných dimenzionálních reprezentací skutečných a složitých Lieových algeber a Lieových skupin jsou dány vzorcem Weylových znaků . Rozměry nejmenších neredukovatelných reprezentací jsou (sekvence A104599 v OEIS ):

1, 7, 14, 27, 64, 77 (dvakrát), 182, 189, 273, 286, 378, 448, 714, 729, 748, 896, 924, 1254, 1547, 1728, 1729, 2079 (dvakrát), 2261, 2926, 3003, 3289, 3542, 4096, 4914, 4928 (dvakrát), 5005, 5103, 6630, 7293, 7371, 7722, 8372, 9177, 9660, 10206, 10556, 11571, 11648, 12096, 13090…

14-dimenzionální reprezentace je reprezentace přidružená a 7-dimenzionální je působení G ₂ na imaginární octoniony.

Existují dvě neizomorfní neredukovatelné reprezentace rozměrů 77, 2079, 4928, 30107 atd. Základní reprezentace jsou ty s rozměry 14 a 7 (odpovídající dvěma uzlům v Dynkinově diagramu v takovém pořadí, že trojitá šipka ukazuje od první až druhý).

Vogan (1994) popsal (nekonečně dimenzionální) unitární neredukovatelné reprezentace rozdělené skutečné formy G ₂ .

Konečné skupiny

Skupina G ₂ ( q ) je body algebraické skupiny G ₂ nad konečným polem F _q . Tyto konečné skupiny poprvé představil Leonard Eugene Dickson v Dickson (1901) pro liché q a Dickson (1905) pro sudé q . Pořadí G ₂ ( q ) je q ⁶ ( q ⁶ - 1) ( q ² - 1) . Když q ≠ 2 , skupina je jednoduchá , a když q = 2 , má jednoduchou podskupinu indexu 2 izomorfní na ² A ₂ (3 ² ) a je to skupina automorfismu maximálního řádu oktonionů. Skupina Janko J ₁ byla nejprve konstruována jako podskupina G ₂ (11). Ree (1960) představil zkroucené Reeovy skupiny ² G ₂ ( q ) řádu q ³ ( q ³ + 1) ( q - 1) pro q = 3 ^{2 n +1} , lichá mocnina 3.

Viz také

• Kartanová matice
• Dynkinův diagram
• Výjimečná Jordanova algebra
• Zásadní reprezentace
• G ₂ -struktura
• Skupina lži
• Sedmimenzionální křížový produkt
• Prostá skupina Lie

Reference

• Adams, J. Frank (1996), Přednášky o výjimečných Lieových skupinách , Chicago Lectures in Mathematics, University of Chicago Press , ISBN 978-0-226-00526-3, MR  1428422
• Baez, John (2002), "The Octonions", Bull. Amer. Matematika. Soc. , 39 (2): 145–205, arXiv : matematika/0105155 , doi : 10,1090/S0273-0979-01-00934-X.

Viz část 4.1: G ₂ ; online verze HTML je k dispozici na adrese http://math.ucr.edu/home/baez/octonions/node14.html .

• Bryant, Robert (1987), „Metriky s výjimečnou holonomií“, Annals of Mathematics , 2, 126 (3): 525–576, doi : 10,2307/1971360 , JSTOR  1971360
• Dickson, Leonard Eugene (1901), „Theory of Linear Groups in An arbitrary Field“, Transactions of the American Mathematical Society , Providence, RI: American Mathematical Society , 2 (4): 363–394, doi : 10,1090/S0002-9947 -1901-1500573-3 , ISSN  0002-9947 , JSTOR  1986251 , Přetištěno ve svazku II jeho sebraných papírůLeonard E. Dickson hlásil skupiny typu G ₂ v oblastech lichých charakteristik.
• Dickson, LE (1905), „Nový systém jednoduchých skupin“ , Math. Ann. , 60 : 137–150, doi : 10,1007/BF01447497Leonard E. Dickson hlásil skupiny typu G ₂ v polích sudých charakteristik.
• Ree, Rimhak (1960), „Rodina jednoduchých skupin spojených s jednoduchou Lieovou algebrou typu (G ₂ )“, Bulletin of American Mathematical Society , 66 (6): 508–510, doi : 10,1090/S0002-9904 -1960-10523-X , ISSN  0002-9904 , MR  0125155
• Vogan, David A. Jr. (1994), "The unitary dual of G ₂ ", Inventiones Mathematicae , 116 (1): 677–791, Bibcode : 1994InMat.116..677V , doi : 10.1007/BF01231578 , ISSN  0020- 9910 , MR  1253210