Zákony formy -Laws of Form
Zákony formy (dále jen LoF ) je kniha G. Spencer-Browna , publikovaná v roce 1969, která překračuje hranice mezi matematikou a filozofií . LoF popisuje tři odlišné logické systémy :
- „Primární aritmetika“ (popsaná v kapitole 4 LoF ), jejíž modely zahrnují logickou aritmetiku ;
- „Primární algebra “ (kapitola 6 LoF ), jejíž modely zahrnují dvouprvkovou booleovskou algebru (dále zkráceně 2 ), logickou logiku a klasický výrokový kalkul ;
- „Rovnice druhého stupně“ (kapitola 11), jejichž interpretace zahrnují konečné automaty a omezenou rekurzivní aritmetiku (RRA) Alonzo Church .
„Boundary algebra“ je Meguireův (2011) výraz pro spojení primární algebry a primární aritmetiky. Zákony formy někdy volně odkazují na „primární algebru“ i na LoF .
Kniha
Předmluva uvádí, že dílo bylo poprvé prozkoumáno v roce 1959, a Spencer Brown uvádí Bertranda Russella jako podporu jeho úsilí. Rovněž děkuje JCP Millerovi z University College London za pomoc s korekturou a nabídku dalších pokynů. V roce 1963 byl Spencer Brown pozván Harrym Frostem , lektorem fyzikálních věd na katedře mimomurálních studií University of London, aby přednesl kurz matematiky logiky.
LoF vznikl z práce v elektronickém inženýrství, jejíž autor se věnoval kolem roku 1960, az následných přednášek o matematické logice, které uspořádal pod záštitou rozšiřujícího programu University of London . LoF se objevil v několika vydáních. Druhá série vydání se objevila v roce 1972 s „Předmluvou k prvnímu americkému vydání“, která zdůrazňovala použití sebereferenčních paradoxů. nejnovější je německý překlad z roku 1997 a nikdy nevyšel z tisku.
Matematika vyplňuje jen asi 55 procentních bodů a je poněkud základní. Ale mystická a deklamativní próza LoF a její láska k paradoxu z ní činí náročné čtení pro všechny. Spencer-Brown byl ovlivněn Wittgensteinem a RD Laingem . LoF také odráží řadu témat ze spisů Charlese Sanderse Peirce , Bertranda Russella a Alfreda North Whiteheada .
Celá kniha je napsána operativně a dává čtenáři pokyny, místo aby mu říkala, co „je“. V souladu se zájmem G. Spencer-Browna o paradoxy je jedinou větou, která činí prohlášení, že něco je, prohlášení, které říká, že žádná taková prohlášení nejsou v této knize použita. Kromě této jedné věty lze knihu považovat za příklad E-Prime .
Recepce
LoF , který byl zdánlivě dílem formální matematiky a filozofie, se stal kultovním klasikem : ocenil ho Heinz von Foerster, když jej recenzoval pro katalog Celá Země . Ti, kteří souhlasí, poukazují na to, že LoF ztělesňuje záhadnou „matematiku vědomí “, jejíž algebraická symbolika zachycuje (snad i „ten“) implicitní kořen poznání : schopnost „rozlišovat“. LoF tvrdí, že primární algebra odhaluje nápadné souvislosti mezi logikou , booleovskou algebrou a aritmetikou a filozofií jazyka a mysli .
Banaschewski (1977) tvrdí, že primární algebra není nic jiného než nová notace pro booleovskou algebru. Na dvouprvkovou booleovskou algebru 2 lze skutečně pohlížet jako na zamýšlenou interpretaci primární algebry. Přesto zápis primární algebry:
- Plně využívá dualitu charakterizující nejen booleovské algebry, ale všechny svazy ;
- Zdůrazňuje, jak syntakticky odlišné příkazy v logice a 2 mohou mít stejnou sémantiku ;
- Dramaticky zjednodušuje výpočty booleovské algebry a důkazy v sentenciální a sylogistické logice .
Kromě toho lze syntaxi primární algebry rozšířit na formální systémy jiné než 2 a sentenciální logiku, což vede k hraniční matematice (viz § Související práce níže).
LoF ovlivnil mimo jiné Heinze von Foerstera , Louise Kauffmana , Niklase Luhmanna , Humberta Maturanu , Francise Varela a Williama Brickena . Někteří z těchto autorů upravili primární algebru mnoha zajímavými způsoby.
LoF tvrdil, že některé známé velmi dlouhé matematické dohady, jako je čtyřbarevná věta , Fermatova poslední věta a Goldbachova domněnka , jsou prokazatelné pomocí rozšíření primární algebry. Spencer-Brown nakonec rozeslal domnělý důkaz věty o čtyřech barvách, ale setkal se se skepticismem.
Formulář (kapitola 1)
Symbol:
Také se jí říká „značka“ nebo „kříž“, což je základní rys zákonů formy. V nenapodobitelném a záhadném módu Spencer-Browna značka symbolizuje kořen poznání , tj. Dualistická značka označuje schopnost odlišit „toto“ od „všeho jiného než tohoto“.
V LoF označuje kříž kresbu „rozdílu“ a lze jej považovat za označení následujících, najednou:
- Akt kolem něčeho ohraničuje hranice, čímž ji odděluje od všeho ostatního;
- To, co se odlišuje od všeho tím, že kreslí hranici;
- Přechod z jedné strany hranice na druhou.
Všechny tři způsoby znamenají akci ze strany kognitivní entity (např. Osoby), která rozlišuje. Jak říká LoF :
"První příkaz:
- Rozlišujte
lze dobře vyjádřit takovými způsoby, jako jsou:
- Nechť je rozdíl,
- Najděte rozdíl,
- Vidět rozdíl,
- Popište rozdíl,
- Definujte rozdíl,
Nebo:
- Nechte rozlišovat "( LoF , poznámky ke kapitole 2)
Kontrapunktem do Marked stavu je Unmarked state, což je prostě nic, prázdnota nebo nevyslovitelný nekonečno reprezentovaný mezerou. Je to prostě absence kříže. Nerozlišuje se a nic nebylo překročeno. Označený stav a prázdnota jsou dvě primitivní hodnoty zákonů formy.
Kříž lze chápat tak, že označuje rozdíl mezi dvěma státy, jedním „považovaným za symbol“ a druhým ne považovaným. Z této skutečnosti vyvstává podivná rezonance s některými teoriemi vědomí a jazyka . Paradoxně je forma okamžitě pozorovatelem a pozorovatelem a je také tvůrčím aktem provádění pozorování. LoF (kromě zadní hmoty) se uzavírá slovy:
... první rozlišení, značka a pozorovatel jsou nejen zaměnitelné, ale ve své podobě identické.
CS Peirce dospěl k souvisejícímu vhledu v 90. letech 19. století; viz § Související práce .
Primární aritmetika (kapitola 4)
Syntax primárního aritmetiky jde takto. Existují jen dva atomové výrazy :
Existují dvě indukční pravidla:
- Kříž
 může být napsán přes jakýkoli výraz;
může být napsán přes jakýkoli výraz; - Jakékoli dva výrazy mohou být zřetězeny .
Na sémantika primárního aritmetiky jsou snad nic víc než jedinou výslovnou definicí v Lof : „Rozdíl je dokonalá zdrženlivost“.
Nechte „neoznačený stav“ být synonymem pro neplatnost. Prázdný kříž označuje „označený stav“. Kříž je přechod z jedné hodnoty, neoznačeného nebo označeného stavu, na druhou. Nyní můžeme uvést „aritmetické“ axiomy A1 a A2, které uzemňovaly primární aritmetiku (a tedy všechny formové zákony):
„A1. Zákon o volání“. Volání dvakrát ze stavu je nerozeznatelné od volání jednou. Dvakrát rozlišovat má stejný účinek jako jednou rozlišovat. Například vyslovení slova „Budiž světlo“ a následného opakování „Nechť je světlo“ je stejné, jako když to řeknete jednou. Formálně:
„A2. Zákon o křížení“. Po přechodu z neoznačeného do označeného stavu se opětovným přejetím („překřížením“) počínaje od označeného stavu vrátí jeden do neoznačeného stavu. Proto překřížení anuluje křížení. Formálně:
V A1 i A2 má výraz napravo od '=' méně symbolů než výraz nalevo od '='. To naznačuje, že každý primární aritmetický výraz lze opakovanou aplikací A1 a A2 zjednodušit na jeden ze dvou stavů: označený nebo neoznačený stav. Je tomu skutečně tak a výsledkem je „zjednodušení“ výrazu. Dva základní metatefory primárního aritmetického stavu, které:
- Každý konečný výraz má jedinečné zjednodušení. (T3 v LoF );
- Počínaje počátečním označeným nebo neoznačeným stavem nemůže „komplikování“ výrazu konečným počtem opakovaných aplikací A1 a A2 přinést výraz, jehož zjednodušení se liší od počátečního stavu. (T4 v LoF ).
Tak vztah of ekvivalence oddílů všechny základní aritmetické výrazy do dvou tříd ekvivalence : ty, které zjednodušují na kříži, a ty, které zjednodušují do prázdna.
A1 a A2 mají volné analogie ve vlastnostech sériových a paralelních elektrických obvodů a v jiných způsobech diagramovacích procesů, včetně vývojového diagramu. A1 odpovídá paralelnímu připojení a A2 sériovému připojení s tím, že rozlišování odpovídá změně způsobu připojení dvou bodů v obvodu, nikoli pouze přidání kabeláže.
Primární aritmetika je analogická s následujícími formálními jazyky z matematiky a informatiky :
- Dyck jazyk řádu 1 s nulovým abecedy;
- Nejjednodušší bezkontextový jazyk v Chomského hierarchii ;
- Přepsat systém , který je silně normalizaci a splývající .
Fráze „indikace“ v LoF je synonymem pro „primární aritmetiku“.
Pojem kánonu
Pro LoF je charakteristický koncept „kánonu“. Zatímco LoF nedefinuje kánon, následující dva výňatky z Notes to chpt. 2 jsou výstižné:
Důležitějším strukturám velení se někdy říká kánony . Jsou to způsoby, kterými se zdá, že se hlavní pokyny seskupují do konstelací, a nejsou tedy v žádném případě na sobě nezávislé. Kánon nese rozdíl v tom, že je mimo (tj. Popisuje) systém ve výstavbě, ale příkaz ke konstrukci (např. „Rozlišovat“), přestože může mít zásadní význam, není kánonem. Kánon je objednávka nebo soubor objednávek, které mají povolit nebo povolit, ale nikoli konstruovat nebo vytvářet.
... primární forma matematické komunikace není popis, ale příkaz ... Hudba je podobná umělecká forma, skladatel se ani nepokouší popsat soubor zvuků, které má na mysli, natož soubor pocitů, které skrze ně vznikají , ale zapíše si soubor příkazů, které, pokud se jich umělec řídí, mohou vést k reprodukci původní zkušenosti skladatele.
Tyto výňatky se týkají metalogického rozlišení mezi objektovým jazykem , formálním jazykem diskutovaného logického systému a metajazykem , jazykem (často přirozeným jazykem) odlišným od objektového jazyka, který se používá k vystavení a diskusi o objektovém jazyce. Zdá se, že první citát tvrdí, že kánony jsou součástí metajazyka. Zdá se, že druhý citát tvrdí, že výroky v objektovém jazyce jsou v podstatě příkazy adresované čtenáři autorem. Ani jedno tvrzení neplatí ve standardní metalogice.
Primární algebra (kapitola 6)
Syntax
Vzhledem k jakémukoli platnému primárnímu aritmetickému výrazu vložte na jedno nebo více míst libovolný počet latinských písmen nesoucích nepovinné číselné indexy; výsledkem je vzorec primární algebry . Písmena tak použitá v matematice a logice se nazývají proměnné . Proměnná primární algebry označuje místo, kde lze zapsat primitivní hodnotu ![]() nebo její doplněk
nebo její doplněk ![]() . Více instancí stejné proměnné označuje více umístění se stejnou primitivní hodnotou.
. Více instancí stejné proměnné označuje více umístění se stejnou primitivní hodnotou.
Pravidla upravující logickou ekvivalenci
Znaménko '=' může spojovat dva logicky ekvivalentní výrazy; výsledkem je rovnice . „Logicky ekvivalentní“ znamená, že oba výrazy mají stejné zjednodušení. Logická ekvivalence je relace ekvivalence nad množinou vzorců primární algebry, která se řídí pravidly R1 a R2. Nechť „C“ a „D“ jsou vzorce, z nichž každý obsahuje alespoň jednu instanci podformule A :
- R1 , Nahrazení rovných . Nahradit jednu nebo více instancí A v C od B , což vede k E . Jestliže A = B , pak C = E .
- R2 , jednotná náhrada . Nahradit všechny výskyty A v C a D, s B . C stává E a D se stává F . Pokud C = D , pak E = F . Pamatujte, že A = B není vyžadováno.
R2 se velmi často používá v demonstracích primární algebry (viz níže), téměř vždy tiše. Tato pravidla jsou běžně vyvolávána v logice a ve většině matematiky, téměř vždy nevědomky.
Primární algebry se skládá z rovnic , tedy páry obecných vzorců, které jsou spojeny infix ‚=‘. R1 a R2 umožňují transformaci jedné rovnice na druhou. Proto je primárním algebra je Ekvacionální formální systém, stejně jako mnoho algebraických struktur , včetně Booleovy algebry , které jsou odrůdy . Rovnicová logika byla běžná před Principia Mathematica (např. Peirce, 1,2,3 Johnson 1892) a má dnešní obhájce (Gries a Schneider 1993).
Konvenční matematická logika se skládá z tautologických vzorců, které signalizuje prefixovaný turniket . Chcete-li naznačit, že vzorec A primární algebry je tautologie , jednoduše napište „ A = “. Jestliže jeden nahrazuje ‚=‘ v R1 a R2 s biconditional , výsledné pravidla drží v konvenční logiky. Konvenční logika se však spoléhá hlavně na pravidlo modus ponens ; konvenční logika je tedy potenciální . Rovnostně-ponenciální dichotomie destiluje mnoho z toho, co odlišuje matematickou logiku od zbytku matematiky.
![]()
Iniciály
Počáteční je primární algebry rovnice ověřitelný prostřednictvím rozhodovacím postupem a jako takový je není axiom . LoF stanoví iniciály:
|
|
=. |
Absence čehokoli napravo od „=“ výše je úmyslná.
|
|
C | = |
|
. |
J2 je obeznámen distributivní zákon o větné logiky a Booleova algebra .
Další sada iniciál, přátelštější k výpočtům, je:
|
|
A | = | A. |
|
|
= |
|
. |
|
A |
|
= | A |
|
. |
Je to díky C2 , že primární algebra je mříž . Na základě J1a se jedná o doplněnou mříž, jejíž horní mez je ![]() . Tím, J0 ,
. Tím, J0 , ![]() je odpovídající dolní mez a element identity . J0 je také algebraická verze A2 a objasňuje smysl
je odpovídající dolní mez a element identity . J0 je také algebraická verze A2 a objasňuje smysl ![]() aliasů s prázdnou stránkou.
aliasů s prázdnou stránkou.
T13 v LoF zobecňuje C2 následovně. Libovolný vzorec B primární algebry (nebo sentenciální logiky) lze zobrazit jako uspořádaný strom s větvemi . Pak:
T13 : od A podformule lze kopírovat podle libosti do libovolné hloubce B větší než A , pokud a jeho kopie jsou ve stejné větvi B . Vzhledem k tomu, že existuje více instancí A ve stejné větvi B , jsou všechny instance kromě těch nejmělčích nadbytečné.
Zatímco důkaz T13 by vyžadoval indukci , intuice, která je jeho základem, by měla být jasná.
C2 nebo jeho ekvivalent se jmenuje:
- „Generace“ v LoF ;
- „Vyloučení“ v Johnsonovi (1892);
- „Pervaze“ v díle Williama Brickena.
Možná, že první příklad axiom nebo pravidlo o výkonu C2 byl „pravidlo (DE) iterace“, kombinující T13 a AA = A , z CS Peirce je existenční grafů .
LoF tvrdí, že zřetězení lze ve výchozím nastavení číst jako dojíždění a přidružování, a proto není nutné jej výslovně předpokládat ani demonstrovat. (Peirce učinil podobné tvrzení o svých existenčních grafech .) Nechť je období dočasným zápisem k vytvoření seskupení. Že zřetězení dojíždějící a spolupracovníci lze poté prokázat z:
- Počáteční AC.D = CD.A a důsledek AA = A (Byrne 1946). Tento výsledek platí pro všechny mřížky , protože AA = A je snadným důsledkem absorpčního zákona , který platí pro všechny mřížky;
- Iniciály AC.D = AD.C a J0 . Protože J0 platí pouze pro mřížky se spodní mezí, tato metoda platí pouze pro ohraničené mřížky (které zahrnují primární algebru a 2 ). Komutativita je triviální; stačí nastavit A =
 . Asociativita: AC.D = CA.D = CD.A = A.CD .
. Asociativita: AC.D = CA.D = CD.A = A.CD .
Po prokázání asociativity může být období zahozeno.
Iniciály v Meguire (2011) jsou AC.D = CD.A , nazvané B1 ; B2 , J0 výše; B3 , Jla výše; a B4 , C2. Podle návrhu jsou tyto iniciály velmi podobné axiómům pro abelianskou skupinu , G1-G3 níže.
Teorie důkazů
Primární algebra obsahuje tři druhy prokázaly tvrzení:
- Důsledkem je primární algebraická rovnice ověřená demonstrací . Demonstrace se skládá z posloupnosti kroků , přičemž každý krok je ospravedlněn počátečním nebo dříve prokázaným důsledkem.
- Věta je výrok v metajazyku ověřený důkazem , tj. Argumentem formulovaným v metajazyku, který je přijat vyškolenými matematiky a logiky.
- Počáteční , definováno výše. Demonstrace a důkazy vyvolávají iniciálu, jako by to byl axiom.
Rozdíl mezi důsledkem a větou platí pro všechny formální systémy, včetně matematiky a logiky, ale obvykle to není výslovné. Demonstrační nebo rozhodovací postup lze provést a ověřit počítačem. Důkaz o věta nemůže být.
Nechť A a B jsou vzorce primární algebry . Demonstrace A = B může probíhat dvěma způsoby:
- Upravujte A v krocích, dokud se nezíská B , nebo naopak;
- Zjednodušit oba
 i
i 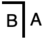 se
se  . Toto se nazývá „výpočet“.
. Toto se nazývá „výpočet“.
Jakmile je A = B předvedeno, lze A = B vyvolat k ospravedlnění kroků v následujících demonstracích. Demonstrace a výpočty primární algebry často nevyžadují více než J1a , J2 , C2 a důsledky ![]() ( C3 v LoF ),
( C3 v LoF ), ![]() ( C1 ) a AA = A ( C5 ).
( C1 ) a AA = A ( C5 ).
Důsledek 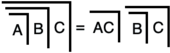 , C7 ' v LoF , umožňuje algoritmus načrtnutý v důkazu LoF s T14, který transformuje libovolný vzorec primární algebry na ekvivalentní vzorec, jehož hloubka nepřesahuje dvě. Výsledkem je normální forma , primární algebraický analog konjunktivní normální formy . LoF (T14–15) dokazuje primární algebraický analog známé booleovské věty o tom, že každý vzorec má normální formu.
, C7 ' v LoF , umožňuje algoritmus načrtnutý v důkazu LoF s T14, který transformuje libovolný vzorec primární algebry na ekvivalentní vzorec, jehož hloubka nepřesahuje dvě. Výsledkem je normální forma , primární algebraický analog konjunktivní normální formy . LoF (T14–15) dokazuje primární algebraický analog známé booleovské věty o tom, že každý vzorec má normální formu.
Nechť být podformule nějakého vzorce B . V kombinaci s C3 , J1a lze považovat za podmínky, uzavírací pro výpočty: B je tautologie právě tehdy, když a ( ) jak se objeví v hloubce 0 z B . Související podmínka se objevuje v některých verzích přirozené dedukce . Demonstrace výpočtem je často o něco více než:
- Opakované vyvolání T13 k odstranění nadbytečných podformulí;
- Vymazání všech podformulí, které mají formu
 .
.
Poslední krok výpočtu vždy vyvolá J1a .
LoF obsahuje nové elegantní důkazy o následující standardní metateorii :
- Úplnost : všechny primární důsledky algebry jsou prokazatelné z iniciál (T17).
- Nezávislost : J1 nelze prokázat z J2 a naopak (T18).
Tato sentenciální logika je úplná, se vyučuje v každém prvním kurzu univerzity v matematické logice . Ale univerzitní kurzy booleovské algebry málokdy zmiňují úplnost 2 .
Výklady
Pokud jsou stavy Marked a Unmarked čteny jako booleovské hodnoty 1 a 0 (nebo True a False ), bude primární algebra interpretovat 2 (nebo logiku sentential ). LoF ukazuje, jak může primární algebra interpretovat sylogismus . Každá z těchto interpretací je popsána v podsekci níže. Prodlužuje primární algebry , aby mohl interpretovat standardní logiku prvního řádu je třeba ještě udělat, ale Peirce ‚s beta existenciální grafy ukazují, že toto rozšíření je proveditelné.
Dvouprvková booleovská algebra 2
Primární algebry je elegantní minimalistické zápis pro Dvouprvkové booleovské algebry 2 . Nechat:
- Jeden z booleovských spojení (+) nebo meet (×) interpretuje zřetězení ;
- Doplňkem of A interpretovat
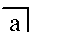
- 0 (1) interpretuje prázdnou značku, pokud join (meet) interpretuje zřetězení (protože binární operaci aplikovanou na nula operandů lze považovat za stejnou jako prvek identity této operace; nebo jinak řečeno, operand, který je chybějící může být standardně považováno za jednající jako prvek identity).
Pokud join (meet) interpretuje AC , pak meet (join) interpretuje . Proto je primární algebry a 2 jsou isomorfní, ale na jeden detail: primární algebry doplnění může být nullary, přičemž v tomto případě označuje primitivní hodnotu. Modulo tento detail, 2 je model primární algebry. Primární aritmetika navrhuje následující aritmetickou axiomatizaci 2 : 1 + 1 = 1 + 0 = 0 + 1 = 1 = ~ 0 a 0 + 0 = 0 = ~ 1.
Sada je Booleovská domény nebo nosič . V jazyce univerzální algebře je primární algebra je algebraická struktura typu . Expresivní přiměřenost na Sheffer zdvihu poukazuje na primární algebra také být algebra typu . V obou případech jsou identity J1a, J0, C2 a ACD = CDA . Protože primární algebra a 2 jsou izomorfní , lze 2 považovat za algebru typu . Tento popis 2 je jednodušší než ten běžný, jmenovitě algebra typu .
![]()
![]()
Tyto dvě možné interpretace jsou navzájem dvojí v booleovském smyslu. (V booleovské algebře získá výměna AND ↔ OR a 1 ↔ 0 v celé rovnici stejně platnou rovnici.) Identity zůstávají invariantní bez ohledu na to, která interpretace je zvolena, takže transformace nebo způsoby výpočtu zůstávají stejné; pouze interpretace každého formuláře by byla odlišná. Příklad: J1a je ![]() . Interpretace juxtapozice jako OR a
. Interpretace juxtapozice jako OR a ![]() jako 1, to znamená, že je to pravda. Interpretace juxtapozice jako AND a jako 0, to znamená, že je to také pravda (a dvojí ).
jako 1, to znamená, že je to pravda. Interpretace juxtapozice jako AND a jako 0, to znamená, že je to také pravda (a dvojí ).
![]()
Sentenční logika
Nechte prázdnou stránku označit False a nechte křížek číst jako Ne . Pak má primární aritmetika následující sentenciální čtení:
- = False
Primární algebra interpretuje větné logiku takto. Písmeno představuje jakýkoli daný sentenciální výraz. Tím pádem:
|
, |
|
jak interpretovat A právě tehdy, když B nebo A je ekvivalentní B . |
Jakýkoli výraz v sentenciální logice má tedy primární překlad algebry . Ekvivalentně primární algebra interpretuje sentenciální logiku. Vzhledem k přiřazení každé proměnné ke stavům Marked nebo Unmarked se tento primární překlad algebry redukuje na primární aritmetický výraz, který lze zjednodušit. Opakováním tohoto cvičení pro všechna možná přiřazení dvou primitivních hodnot ke každé proměnné odhalíte, zda je původní výraz tautologický nebo uspokojivý . Toto je příklad rozhodovacího postupu , který je víceméně v duchu konvenčních tabulek pravdy. Vzhledem k primárnímu algebrickému vzorci obsahujícímu N proměnných vyžaduje tento rozhodovací postup zjednodušení 2 N primárních aritmetických vzorců. Pro méně únavné rozhodovacího procesu více v duchu Quine ‚analýzy pravdivostní hodnota‘ ‚s, viz Meguire (2003).
Schwartz (1981) dokázal, že primární algebra je ekvivalentní - syntakticky , sémanticky a důkaz teoreticky - s klasickým výrokovým kalkulem . Podobně lze ukázat, že primární algebra je syntakticky ekvivalentní s výrazy vytvořenými obvyklým způsobem z klasických hodnot pravdy true a false , logických spojek NOT, OR a AND a závorek.
Interpretace neoznačeného státu jako nepravdivá je zcela svévolná; tento stav lze stejně dobře číst jako True . Vyžaduje se pouze to, aby se interpretace zřetězení změnila z OR na AND. KDYŽ A POTOM B se nyní překládá jako ![]() místo
místo ![]() . Obecněji je primární algebra „sebe- duální “, což znamená, že jakýkoli vzorec primární algebry má dvě věty nebo booleovské hodnoty, každé z nich je dvojí . Dalším důsledkem sebe-duality je irelevance zákonů De Morgana ; tyto zákony jsou od začátku zabudovány do syntaxe primární algebry .
. Obecněji je primární algebra „sebe- duální “, což znamená, že jakýkoli vzorec primární algebry má dvě věty nebo booleovské hodnoty, každé z nich je dvojí . Dalším důsledkem sebe-duality je irelevance zákonů De Morgana ; tyto zákony jsou od začátku zabudovány do syntaxe primární algebry .
Nyní se ukazuje skutečná podstata rozdílu mezi primární algebrou na jedné straně a 2 a sentenciální logikou na straně druhé. V posledních formalizmech není komplementace / negace fungující na „ničem“ dobře utvářena. Prázdný kříž je ale dobře vytvořený výraz primární algebry , označující označený stav, primitivní hodnotu. Neprázdný kříž je tedy operátor , zatímco prázdný kříž je operand, protože označuje primitivní hodnotu. Tak primární algebry ukazuje, že až dosud různé matematické pojmy provozovatele a operandů jsou ve skutečnosti pouze různé aspekty jedné základní akce, Zhotovení rozdílu.
Sylogismy
Příloha 2 LoF ukazuje, jak převést tradiční sylogismy a sority do primární algebry . Platný sylogismus je jednoduše ten, jehož primární překlad algebry se zjednoduší na prázdný kříž. Nechť A * označuje doslovný , tj. Buď A nebo , lhostejně. Pak každý sylogismus, který nevyžaduje, aby jeden nebo více výrazů bylo považováno za neprázdný, je jednou z 24 možných permutací zobecnění Barbary, jejíž primární ekvivalent algebry je . Těchto 24 možných permutací zahrnuje 19 sylogistických forem považovaných za platné v aristotelské a středověké logice . Tento primární překlad algebry sylogistické logiky také naznačuje, že primární algebra může interpretovat monadickou a termínovou logiku a že primární algebra má spřízněnost s booleovským termínovým schématem Quina (1982: Část II).
Příklad výpočtu
Následující výpočet Leibnizovy netriviální Praeclarumovy věty ilustruje demonstrativní sílu primární algebry . Nechť C1 je = A , C2 je , C3 je , J1a je a nechme OI znamenat, že proměnné a podformule byly přeuspořádány způsobem, který umožňuje komutativita a asociativita.
| [( P → R ) ∧ ( Q → S )] → [( P ∧ Q ) → ( R ∧ S )]. | Věta Praeclarum . | ||||||||||||||||||||||
|
primární překlad algebry | ||||||||||||||||||||||
|
C1. | ||||||||||||||||||||||
|
C1. | ||||||||||||||||||||||
|
OI. | ||||||||||||||||||||||
|
C2. | ||||||||||||||||||||||
|
OI. | ||||||||||||||||||||||
|
C2. | ||||||||||||||||||||||
|
OI. | ||||||||||||||||||||||
|
C2. | ||||||||||||||||||||||
|
C1. | ||||||||||||||||||||||
|
OI. | ||||||||||||||||||||||
|
J1a. | ||||||||||||||||||||||
|
OI. | ||||||||||||||||||||||
|
C3. |
Vztah k magmatům
Primární algebry ztělesňuje bod upozornění pro Huntington v roce 1933: Booleovská algebra vyžaduje, kromě jedné unární operaci , jeden, a ne dva, binární operace . Proto je zřídka známá skutečnost, že booleovské algebry jsou magma . (Magmatům se říkalo grupoidy, dokud si druhý termín nepřivlastnil teorie kategorií .) Chcete-li to vidět, všimněte si, že primární algebra je komutativní :
- Poloskupina, protože juxtapozice primární algebry dojíždí a sdružuje se ;
-
Monoid s prvkem identity
 na základě J0 .
na základě J0 .
Skupiny také vyžadují unární operaci nazvanou inverzní , protějšek skupiny booleovské komplementace . Dovolit ![]() značí inverzní . Nechť značí skupinu identity prvek . Skupiny a primární algebra pak mají stejné podpisy , jmenovitě jsou to obě algebry typu 〈2,1,0〉. Proto je primární algebry je hranice algebry . Axiomy pro abelianskou skupinu v hraniční notaci jsou:
značí inverzní . Nechť značí skupinu identity prvek . Skupiny a primární algebra pak mají stejné podpisy , jmenovitě jsou to obě algebry typu 〈2,1,0〉. Proto je primární algebry je hranice algebry . Axiomy pro abelianskou skupinu v hraniční notaci jsou:
![]()
Z G1 a G2 lze odvodit komutativitu a asociativitu zřetězení, jak je uvedeno výše. Všimněte si, že G3 a J1a jsou identické. G2 a J0 by byly identické, kdyby ![]() =
= ![]() nahradil A2 . Toto je definující aritmetická identita teorie grup v hraniční notaci.
nahradil A2 . Toto je definující aritmetická identita teorie grup v hraniční notaci.
Primární algebry liší od abelian skupiny dvěma způsoby:
- Z A2 vyplývá, že
 ≠
≠  . Pokud by primární algebra byla skupina ,
. Pokud by primární algebra byla skupina ,  =
=  by platilo a jedna z a = nebo a = a by musela být důsledkem primární algebry . Všimněte si, že a jsou vzájemné primární algebry doplňují, jak to vyžaduje teorie skupin, takže to platí jak pro teorii skupin, tak pro primární algebru ;
by platilo a jedna z a = nebo a = a by musela být důsledkem primární algebry . Všimněte si, že a jsou vzájemné primární algebry doplňují, jak to vyžaduje teorie skupin, takže to platí jak pro teorii skupin, tak pro primární algebru ;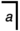




- C2 nejjasněji vymezuje primární algebru od ostatních magmat, protože C2 umožňuje demonstrovat absorpční zákon, který definuje mřížky , a distribuční zákon centrální vůči booleovské algebře .
Jak A2, tak C2 vyplývají z toho, že B je objednaná množina .
Rovnice druhého stupně (kapitola 11)
Kapitola 11 LoF zavádí rovnice druhého stupně , složené z rekurzivních vzorců, které lze považovat za „nekonečnou“ hloubku. Některé rekurzivní vzorce se zjednodušují do označeného nebo neoznačeného stavu. Jiní mezi těmito dvěma stavy „oscilují“ neomezeně podle toho, zda je daná hloubka sudá nebo lichá. Konkrétně určité rekurzivní vzorce lze interpretovat jako oscilaci mezi pravdou a nepravdou v po sobě jdoucích časových intervalech, v takovém případě se má za to, že vzorec má „imaginární“ hodnotu pravdy. Tok času tak může být zaveden do primární algebry .
Turney (1986) ukazuje, jak lze tyto rekurzivní vzorce interpretovat pomocí omezené rekurzivní aritmetiky (RRA) Alonzo Church . Church představil RRA v roce 1955 jako axiomatickou formalizaci konečných automatů . Turney (1986) představuje obecnou metodu převodu rovnic druhého stupně do Church's RRA, ilustrující jeho metodu pomocí vzorců E1 , E2 a E4 v kapitole 11 LoF . Tento překlad do RRA osvětluje jména, která dal Spencer-Brown E1 a E4 , jmenovitě „paměť“ a „počitadlo“. RRA tedy formalizuje a objasňuje pojem LoF o imaginární hodnotě pravdy.
Související práce
Gottfried Leibniz , v memorandech, která nebyla zveřejněna před koncem 19. a začátkem 20. století, vynalezl logickou logiku . Jeho zápis byl isomorphic k tomu Lof : zřetězení číst jako spojení , a „ne ( X )“ číst jako doplněk z X . Uznání průkopnické role Leibnize v algebraické logice předznamenali Lewis (1918) a Rescher (1954). Úplné zhodnocení Leibnizových úspěchů však muselo čekat na dílo Wolfganga Lenzena, publikované v 80. letech a přezkoumané v Lenzen (2004).
Charles Sanders Peirce (1839–1914) očekával primární algebru ve třech pracovních žilách:
- Dva dokumenty, které napsal v roce 1886, navrhly logickou algebru využívající pouze jeden symbol, streamer , téměř totožný s křížem LoF . Sémantika streameru je totožná se sémantikou kříže, až na to, že Peirce nikdy nenapsal streamer, pod kterým by nic nebylo. Výňatek z jednoho z těchto článků byl publikován v roce 1976, ale v plném rozsahu byly publikovány až v roce 1993.
- V článku encyklopedie z roku 1902 Peirce notoval booleovskou algebru a sentenciální logiku způsobem tohoto záznamu, kromě toho, že používal dva styly závorek, přepínající mezi „(',') 'a' [','] 's každým přírůstkem v hloubka vzorce.
- Syntax jeho alfa existenčních grafů je jen zřetězení , číst jako spojení a skříni ovály, číst jako negaci . Pokud se zřetězení primární algebry čte jako konjunkce , pak jsou tyto grafy izomorfní s primární algebrou (Kauffman 2001).
Je ironií, že LoF cituje sv. 4 Peirce's Collected Papers, zdroj pro formalizmy v (2) a (3) výše. (1) - (3) byly prakticky neznámé v době, kdy (šedesátá léta) a na místě, kde byla napsána (UK) LoF . Peirceova semiotika , o které LoF mlčí, může ještě osvětlit filozofické aspekty LoF .
Kauffman (2001) pojednává o dalším zápisu podobném zápisu LoF , o článku z roku 1917 Jeana Nicoda , který byl žákem Bertranda Russella .
Výše uvedené formalizmy jsou, stejně jako primární algebra , všechny případy hraniční matematiky , tj. Matematiky, jejíž syntaxe je omezena na písmena a závorky (uzavírací zařízení). Minimalistická syntaxe této povahy je „hraniční notace“. Hraniční notace neobsahuje operátorské symboly infix , prefix nebo postfix . Velmi dobře známé složené závorky ('{', '}') teorie množin lze považovat za hraniční notaci.
Práce Leibnize, Peirce a Nicoda je nevinná v metateorii, jak psali před mezníkem z roku 1920 Emila Posta (který LoF uvádí), což dokazuje, že sentenciální logika je úplná, a než Hilbert a Łukasiewicz ukázali, jak dokázat nezávislost axiomu pomocí modely .
Craig (1979) tvrdil, že svět a způsob, jakým lidé tento svět vnímají a ovlivňují, má bohatou booleovskou strukturu. Craig byl ortodoxní logik a autor algebraické logiky .
Kognitivní věda druhé generace se objevila v 70. letech, po napsání LoF . O kognitivní vědě a jejím významu pro booleovskou algebru, logiku a teorii množin viz Lakoff (1987) (viz položky rejstříku v části „Příklady schématu obrazu: kontejner“) a Lakoff a Núñez (2001). Ani jedna kniha neuvádí LoF .
Biologové a kognitivní vědci Humberto Maturana a jeho student Francisco Varela diskutují o LoF ve svých spisech, které označují „rozdíl“ jako základní kognitivní akt. Psychologka a kognitivní vědkyně z Berkeley Eleanor Rosch rozsáhle psala o úzce souvisejícím pojmu kategorizace.
Mezi další formální systémy s možnou afinitou k primární algebře patří:
- Mereologie, která má obvykle mřížkovou strukturu velmi podobnou booleovské algebře. Po dobu několika autorů, mereologie je prostě modelem z Booleovy algebry a tedy primární algebry stejně.
- Mereotopologie , která je ze své podstaty bohatší než booleovská algebra;
- Systém Whiteheada (1934), jehož základním primitivem je „indikace“.
Primární aritmetika a algebra jsou minimalistický formalismus pro sentenciální logiku a booleovskou algebru. Jiné minimalistické formalizmy, které mají sílu teorie množin, zahrnují:
- Lambda počet ;
- Kombinační logika se dvěma ( S a K ) nebo dokonce jedním ( X ) primitivním kombinátorem;
- Matematická logika vytvořená pouze se třemi primitivními pojmy: jeden pojivový, NAND (jehož primární překlad algebry je nebo, dvojím způsobem ), univerzální kvantifikace a jeden binární atomový vzorec označující členství v množině . Toto je systém Quine (1951).
- K beta existenciální grafy , s jediným binárním predikátu označujícího set členů. To je ještě třeba prozkoumat. Tyto alfa grafy uvedené výše jsou zvláštní případ z beta grafů.
Viz také
- Booleova algebra (jednoduchá anglická Wikipedia)
- Booleova algebra (úvod)
- Booleova algebra (logika)
- Booleova algebra (struktura)
- Booleovské algebry kanonicky definovány
- Logická logika
- Entitativní graf
- Existenciální graf
- Seznam témat booleovské algebry
- Výrokový počet
- Dvouprvková booleovská algebra
Poznámky
Reference
- Vydání zákonů formy :
- 1969. London: Allen & Unwin, vázaná kniha.
- 1972. Crown Publishers, vázaná kniha: ISBN 0-517-52776-6
- 1973. Knihy Bantam, brožovaná kniha. ISBN 0-553-07782-1
- 1979. EP Dutton, brož. ISBN 0-525-47544-3
- 1994. Portland OR: Cognizer Company, brožovaná kniha. ISBN 0-9639899-0-1
- 1997 německý překlad s názvem Gesetze der Form . Lübeck: Bohmeier Verlag. ISBN 3-89094-321-7
- 2008 Bohmeier Verlag, Lipsko, 5. mezinárodní vydání. ISBN 978-3-89094-580-4
- Bostock, David, 1997. Intermediate Logic . Oxford Univ. Lis.
- Byrne, Lee, 1946, „Dvě formulace booleovské algebry“, Bulletin Americké matematické společnosti : 268–71.
- Craig, William (1979). "Logická logika a každodenní fyzický svět". Sborník a adresy Americké filozofické asociace . 52 (6): 751–78. doi : 10,2307 / 3131383 . JSTOR 3131383 .
- David Gries a Schneider, FB, 1993. Logický přístup k diskrétní matematice . Springer-Verlag.
- William Ernest Johnson , 1892, „Logický počet“, 1. mysl (ns): 3–30.
- Louis H. Kauffman , 2001, „ The Mathematics of CS Peirce “, Cybernetics and Human Knowing 8: 79–110.
- ------, 2006, „ Reformulace věty o barevné mapě “.
- ------, 2006a. „ Zákony formy - průzkum v matematice a nadacích. “ Návrh knihy (tedy velký).
- Lenzen, Wolfgang, 2004, „ Leibnizova logika “ v publikaci Gabbay, D., a Woods, J., ed., The Rise of Modern Logic: From Leibniz to Frege (Handbook of the History of Logic - Vol. 3) . Amsterdam: Elsevier, 1–83.
- Lakoff, George , 1987. Ženy, oheň a nebezpečné věci . University of Chicago Press.
- -------- a Rafael E. Núñez , 2001. Odkud pochází matematika : Jak vtělená mysl přináší matematiku do bytí . Základní knihy.
- Meguire, PG (2003). „Objevování hraniční algebry: zjednodušená notace pro booleovskou algebru a funktory pravdy“. International Journal of General Systems . 32 : 25–87. CiteSeerX 10.1.1.106.634 . doi : 10.1080 / 0308107031000075690 . S2CID 9460101 .
- --------, 2011. Hraniční algebra: jednodušší přístup k základní logice a booleovské algebře . VDM Publishing Ltd. ISBN 978-3639367492 . Zdroj pro většinu této položky, včetně notace, která uzavírá v závorkách, co LoF umístí pod kříž. Vyhýbá se spekulativnějším aspektům LoF .
- Willard Quine , 1951. Mathematical Logic , 2. vyd. Harvard University Press.
- --------, 1982. Methods of Logic , 4. vyd. Harvard University Press.
- Rescher, Nicholas (1954). „Leibnizova interpretace jeho logických kalkulů“ . Journal of Symbolic Logic . 18 (1): 1–13. doi : 10,2307 / 2267644 . JSTOR 2267644 . S2CID 689315 .
- Schwartz, Daniel G. (1981). „Isomorphisms of G. Spencer-Brown's of Laws of Form and F. Varela's Calculus for Self-Reference“. International Journal of General Systems . 6 (4): 239–55. doi : 10.1080 / 03081078108934802 .
- Turney, PD (1986). " Zákony formy a konečné automaty". International Journal of General Systems . 12 (4): 307–18. doi : 10,1080 / 03081078608934939 .
- AN Whitehead , 1934, „Indikace, třídy, počet, ověření“, Mysl 43 (ns): 281–97, 543. Opravy na str. 543 jsou četné a důležité a pozdější dotisky tohoto článku je nezahrnují.
- Dirk Baecker (ed.) (1993), Kalkül der Form. Suhrkamp; Dirk Baecker (ed.), Probleme der Form . Suhrkamp.
- Dirk Baecker (ed.) (1999), Problémy formy , Stanford University Press.
- Dirk Baecker (ed.) (2013), A Mathematics of Form, A Sociology of Observers , Cybernetics & Human Knowing, sv. 20, č. 3-4 .
externí odkazy
- Zákony formy , archiv webových stránek Richarda Shoupa.
- Spencer-Brownovy přednášky v Esalenu, 1973. Samoreferenční formy jsou představeny v části s názvem „Stupeň rovnic a teorie typů“.
- Louis H. Kauffman , „ Box Algebra, hraniční matematika, logika a zákony formy. “
- Kissel, Matthias, „ Nesystematický, ale snadno srozumitelný úvod do zákonů formy . “
- Fórum zákonů o formulářích , kde se od roku 2002 diskutuje o primární algebře a souvisejících formalizmech.
- Setkání s GSB od Moshe Kleina
- Značka Markable , snadný úvod do myšlenek zákonů formy
- BF kalkul a druhá odmocnina negace Louis Kauffman a Arthur Collings; rozšiřuje zákony formy přidáním imaginární logické hodnoty. (Imaginární logické hodnoty jsou uvedeny v kapitole 11 knihy Zákony formy .)
- Kurz zákonů formy - bezplatný online kurz, který provede lidi hlavní částí textu zákonů formy od Leon Conrada, posledního studenta Spencer-Browna, který studoval práci s autorem.

























