Diferenciální geometrie ploch - Differential geometry of surfaces

V matematiky je diferenciální geometrie ploch se zabývá diferenciální geometrie z hladkých povrchů s různými dalšími strukturami, nejčastěji, je Riemannian metrický . Povrchy byly rozsáhle studovány z různých perspektiv: vnější , vztahující se k jejich vložení do euklidovského prostoru a vnitřně , odrážející jejich vlastnosti určené výhradně vzdáleností v povrchu měřenou podél křivek na povrchu. Jedním ze zkoumaných základních konceptů je Gaussovo zakřivení , které nejprve podrobně studoval Carl Friedrich Gauss , který ukázal, že zakřivení je vnitřní vlastností povrchu, nezávislého na jeho izometrickém zakotvení v euklidovském prostoru.
Povrchy přirozeně vznikají grafů z funkcí dvojice proměnných , a někdy se objeví v parametrickém formě nebo jako lokusů spojených s prostorové křivky . Důležitou roli ve své studii byl hrán skupiny lži (v duchu programu Erlangen ), a sice skupin symetrie v euklidovské rovině , na koule a hyperbolického letadla . Tyto Lieovy skupiny lze použít k popisu povrchů konstantního Gaussova zakřivení; poskytují také základní složku moderního přístupu k vlastní diferenciální geometrii prostřednictvím spojení . Na druhé straně byly také rozsáhle studovány vnější vlastnosti závislé na vložení povrchu do euklidovského prostoru. Dobře to ilustrují nelineární Euler-Lagrangeovy rovnice v variačním počtu : ačkoli Euler vyvinul rovnice jedné proměnné, aby porozuměl geodetice , definované nezávisle na vkládání, jedna z Lagrangeových hlavních aplikací těchto dvou proměnných rovnic byla na minimálních plochách , koncept, který lze definovat pouze z hlediska vložení.
Dějiny

Objemy některé povrchy quadric z revoluce byly vypočteny Archimedes . Rozvoj počtu v sedmnáctém století poskytl systematičtější způsob jejich výpočtu. Zakřivení obecných povrchů poprvé studoval Euler . V roce 1760 prokázal vzorec pro zakřivení rovinného řezu povrchu a v roce 1771 uvažoval povrchy reprezentované v parametrické formě. Monge položil základy své teorie ve své klasické monografii L'application de l'analyse à la géometrie, která se objevila v roce 1795. Definující příspěvek k teorii povrchů vytvořil Gauss ve dvou pozoruhodných dokumentech napsaných v letech 1825 a 1827. Tento znamenal nový odklon od tradice, protože Gauss poprvé zvažoval vnitřní geometrii povrchu, vlastnosti, které jsou určeny pouze geodetickými vzdálenostmi mezi body na povrchu nezávisle na konkrétním způsobu, jakým se povrch nachází v okolním euklidovském prostředí prostor. Korunní výsledek, Theorema Egregium of Gauss, prokázal, že Gaussovo zakřivení je vnitřní invariant, tj. Neměnný v místních izometriích . Tento názor byl rozšířen na vícerozměrných prostorech by Riemann a vedl k tomu, co je dnes známý jako Riemannian geometrie . Devatenácté století bylo zlatým věkem teorie povrchů, a to jak z topologického, tak z diferenciálně-geometrického hlediska, přičemž většina předních geometrů se věnovala jejich studiu. Darboux shromáždil mnoho výsledků ve svém čtyřdílném pojednání Théorie des povrchy (1887–1896).
Přehled
Je intuitivně docela známé tvrdit, že list rostliny, povrch skla nebo tvar obličeje jsou určitým způsobem zakřivené a že všechny tyto tvary, i když ignorují jakékoli rozlišovací znaky, mají určitou geometrickou strukturu. funkce, které je odlišují. Diferenciální geometrie povrchů se zabývá matematickým chápáním takových jevů. Studium tohoto oboru, které bylo zahájeno v jeho moderní podobě v 17. století, vedlo k vývoji vyšší dimenzionální a abstraktní geometrie, jako je riemannianská geometrie a obecná relativita .
Základním matematickým objektem je pravidelný povrch. Ačkoli se konvence liší v jejich přesné definici, tvoří obecnou třídu podmnožin trojrozměrného euklidovského prostoru ( ℝ 3 ), které zachycují část známého pojmu „povrch“. Analýzou třídy křivek, které leží na takovém povrchu, a míry, do jaké je povrchy nutí křivit v ℝ 3 , lze ke každému bodu povrchu přiřadit dvě čísla, nazývaná hlavní zakřivení. Jejich průměr se nazývá průměrné zakřivení povrchu a jejich součin se nazývá Gaussovo zakřivení.
Existuje mnoho klasických příkladů pravidelných povrchů, včetně:
- známé příklady, jako jsou letadla, válce a koule
- minimální povrchy , které jsou definovány vlastností, že jejich průměrné zakřivení je v každém bodě nulové. Nejznámějším příkladem jsou catenoids a šroubové plochy , i když mnohé další byly objeveny. Minimální povrchy lze také definovat vlastnostmi souvisejícími s povrchem , což má za následek, že poskytují matematický model pro tvar mýdlových filmů, když jsou nataženy přes drátěný rám
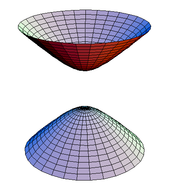
- vládnuté povrchy , což jsou povrchy, které procházejí každým bodem alespoň jednou přímkou; příklady zahrnují válec a hyperboloid jednoho listu.
Překvapivý výsledek Carla Friedricha Gausse , známého jako theorema egregium , ukázal, že Gaussovo zakřivení povrchu, které podle své definice souvisí s tím, jak křivky na povrchu mění směry v trojrozměrném prostoru, lze ve skutečnosti měřit délkami křivek ležících na plochách společně s úhly vytvořenými při protnutí dvou křivek na povrchu. Terminologicky to říká, že Gaussovo zakřivení lze vypočítat z první základní formy (nazývané také metrický tenzor ) povrchu. Druhá základní forma , naopak, je objekt, který kóduje, jak se délky a úhly křivek na povrchu zkreslený, když jsou křivky odrazil povrchu.
Navzdory měření různých aspektů délky a úhlu nejsou první a druhá základní forma na sobě navzájem nezávislé a splňují určitá omezení nazývaná Gauss-Codazziho rovnice . Hlavní věta, často nazývaná základní věta diferenciální geometrie povrchů, tvrdí, že kdykoli dva objekty splní Gaussovo-Codazziho omezení, vzniknou jako první a druhá základní forma pravidelného povrchu.
Pomocí první základní formy je možné definovat nové objekty na pravidelném povrchu. Geodetika jsou křivky na povrchu, které splňují určitou obyčejnou diferenciální rovnici druhého řádu, která je specifikována první základní formou. Jsou velmi přímo spojeny se studiem délek křivek; dostatečně krátkou geodetikou bude vždy křivka nejkratší délky na povrchu, která spojuje její dva koncové body. Geodetika je tedy zásadní pro problém optimalizace určení nejkratší cesty mezi dvěma danými body na pravidelném povrchu.
Lze také definovat paralelní transport podél libovolné dané křivky, což dává předpis, jak deformovat tečný vektor k povrchu v jednom bodě křivky na tečné vektory ve všech ostatních bodech křivky. Předpis je určen obyčejnou diferenciální rovnicí prvního řádu, která je specifikována první základní formou.
Výše uvedené koncepty mají v zásadě vše společného s více proměnným kalkulem. Gauss-Bonnet teorém je větší celkový výsledek, který se týká Gaussian zakřivení povrchu spolu s topologickou typu. Tvrdí, že průměrná hodnota Gaussova zakřivení je zcela určena Eulerovou charakteristikou povrchu spolu s jeho povrchovou plochou.
Pojem Riemannova potrubí a Riemannova povrchu jsou dvě zobecnění pravidelných povrchů diskutovaných výše. Zejména v podstatě všechna zde diskutovaná teorie pravidelných povrchů má zobecnění v teorii riemannianských variet. To neplatí pro povrchy Riemann, ačkoli každý pravidelný povrch uvádí příklad Riemannova povrchu.
Pravidelné povrchy v euklidovském prostoru
Definice
Je intuitivně jasné, že koule je hladká, zatímco kužel nebo pyramida, vzhledem k jejich vrcholům nebo hranám, nejsou. Pojem „pravidelný povrch“ je formalizací pojmu hladkého povrchu. Definice využívá místní reprezentaci povrchu prostřednictvím map mezi euklidovskými prostory . Pro takové mapy existuje standardní představa hladkosti; mapa mezi dvěma otevřenými podmnožinami euklidovského prostoru je hladká, pokud v každém bodě domény existují její dílčí derivace každého řádu.
Následující text uvádí tři ekvivalentní způsoby prezentace definice; střední definice je možná nejvíce vizuálně intuitivní, protože v podstatě říká, že pravidelný povrch je podmnožinou ℝ 3, což je lokálně graf hladké funkce (ať už přes oblast v rovině yz, rovině xz nebo xy letadlo).
| Objekty použité v definici | Pravidelný povrch euklidovské prostor ℝ 3 je podmnožina S of ℝ 3 taková, že každý bod S má ... |
|---|---|
| Místní parametrizace | ... otevřené sousedství U ⊂ S, pro které existuje otevřená podmnožina V o ℝ 2 a homeomorfismus f : V → U takový, že
|
| Mongeovy záplaty | ... otevřené části U ⊂ ℝ 3 , pro které je otevřená podmnožina V z ℝ 2 a hladké funkce h : V → ℝ tak, že jedna z následujících platí:
|
| Implicitní funkce | ... otevřené sousedství U ⊂ ℝ 3, pro které existuje hladká funkce F : U → ℝ s:
|
Tyto homeomorfismy vyskytující se v první definicí jsou známy jako místní parametrizace nebo místními souřadnicových systémů nebo místních grafy na S . Ekvivalence prvních dvou definic tvrdí, že kolem jakéhokoli bodu na pravidelném povrchu vždy existují lokální parametrizace tvaru ( u , v ) ↦ ( h ( u , v ), u , v ) , ( u , v ) ↦ ( u , h ( u , v ), v ) nebo ( u , v ) ↦ ( u , v , h ( u , v )) , známé jako Mongeovy patche. Funkce F jako ve třetí definici se nazývají lokální definující funkce . Ekvivalence všech tří definic vyplývá z věty o implicitní funkci .
Vzhledem k jakýmkoli dvěma lokálním parametrizacím f : V → U a f ′: V ′ → U ′ pravidelného povrchu je kompozice f −1 ∘ f ′ nutně hladká jako mapa mezi otevřenými podmnožinami ℝ 2 . To ukazuje, že jakýkoli pravidelný povrch má přirozeně strukturu hladkého potrubí , přičemž hladký atlas je dán inverzemi místních parametrizací.
V klasické teorii diferenciální geometrie se povrchy obvykle studují pouze v pravidelném případě. Je však také běžné studovat nepravidelné povrchy, ve kterých dvě parciální derivace ∂ u f a ∂ v f lokální parametrizace nemusí být lineárně nezávislé . V tomto případě může mít S singularity, jako jsou cuspidální okraje . Takové povrchy jsou obvykle studovány v teorii singularity . Jiné oslabené formy pravidelných povrchů se vyskytují v počítačově podporovaném designu , kde je povrch rozdělen na nesouvislé kusy, přičemž deriváty místních parametrizací dokonce nejsou spojité podél hranic.
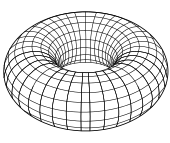
Jednoduché příklady. Jednoduchý příklad pravidelného povrchu udává 2-koule {( x , y , z ) | x 2 + y 2 + z 2 = 1 }; tento povrch lze pokrýt šesti Mongeovými záplatami (dvěma z každého ze tří výše uvedených typů), přičemž h ( u , v ) = ± (1 - u 2 - v 2 ) 1/2 . Lze jej také pokrýt dvěma lokálními parametrizacemi pomocí stereografické projekce . Množina {( x , y , z ): (( x 2 + y 2 ) 1/2 - R ) 2 + z 2 = R 2 } je torus revoluce s poloměry R a R . Je to pravidelný povrch; z formuláře lze zadat místní parametrizaci
Hyperboloid na dva listy {( x , y , z, ): z, 2 = 1 + x 2 + y 2 } je pravidelný povrch; lze jej překrýt dvěma Mongeovými záplatami, přičemž h ( u , v ) = ± (1 + u 2 + v 2 ) 1/2 . Spirálové objeví v teorii minimální povrchů . Je pokryta jedinou lokální parametrizací, f ( u , v ) = ( u sin v , u cos v , v ) .
Tečné vektory a normální vektory
Nechť S být pravidelný povrch ℝ 3 , a nechat p být prvek S . Pomocí jakékoli z výše uvedených definic lze určit určité vektory v ℝ 3 jako tečné k S v p a určité vektory v ℝ 3 jako ortogonální k S v p .
| Objekty použité v definici | Vektor X v ℝ 3 je tečný k S v p, pokud ... | Vektor n v ℝ 3 je normální k S při p, pokud ... |
|---|---|---|
| Místní parametrizace | ... vzhledem k jakékoli lokální parametrizaci f : V → S s p ∈ f ( V ) je X lineární kombinací a | ... je kolmý na každý tečný vektor k S v p |
| Mongeovy záplaty | ... pro jakýkoli patch Monge ( u , v ) ↦ ( u , v , h ( u , v )), jehož rozsah zahrnuje p , jeden má
s parciálními derivacemi vyhodnocenými v bodě ( p 1 , p 2 ) . Analogická definice platí v případě Mongeových záplat ostatních dvou forem. |
... pro jakýkoli patch Monge ( u , v ) ↦ ( u , v , h ( u , v )), jehož rozsah zahrnuje p , n je násobkem ( ∂ h/∂ u, ∂ h/∂ v, −1) podle vyhodnocení v bodě ( p 1 , p 2 ) . Analogická definice platí v případě Mongeových záplat ostatních dvou forem. |
| Implicitní funkce | ... pro libovolnou lokální definující funkci F, jejíž doména obsahuje p , je X ortogonální k ∇ F ( p ) | ... pro libovolnou lokální definující funkci F, jejíž doména obsahuje p , n je násobkem ∇ F ( p ) |
Je vidět, že tečný prostor nebo tečná rovina k S v p , která je definována tak, že se skládá ze všech tečných vektorů k S v p , je dvourozměrný lineární podprostor ℝ 3 ; to je často označován T p S . Normální prostor na S v p , která je definována tak, že se skládají ze všech běžných vektorů na S v p , je jednorozměrný lineární podprostor ℝ 3, který je kolmý na tečnu prostoru T p S . Jako takový, v každém bodě P z S , existují dva normální vektory jednotku délky, nazývané jednotkové normální vektory. Je užitečné poznamenat, že jednotkové normální vektory na p mohou být dány z hlediska místních parametrizací, Mongeových záplat nebo lokálních definujících funkcí prostřednictvím vzorců
podle stejných zápisů jako v předchozích definicích.
Je také užitečné si všimnout „vnitřní“ definice tečných vektorů, která je typická pro zobecnění teorie pravidelných povrchů na nastavení hladkých variet . Definuje tečný prostor jako abstraktní dvourozměrný skutečný vektorový prostor, nikoli jako lineární podprostor ℝ 3 . V této definici se říká, že tečný vektor k S v p je přiřazení každé lokální parametrizace f : V → S s p ∈ f ( V ) dvou čísel X 1 a X 2 , takže pro jakékoli jiné lokální parametrizace f ′: V → S s p ∈ f ( V ) (a s odpovídajícími čísly ( X ′) 1 a ( X ′) 2 ) má
kde A f ′ ( p ) je jakobijská matice mapování f −1 ∘ f ′ , vyhodnocená v bodě f ′ ( p ) . Sbírka tečných vektorů k S v p má přirozeně strukturu dvojrozměrného vektorového prostoru. Tečný vektor v tomto smyslu odpovídá tečnému vektoru v předchozím smyslu uvažováním vektoru
v ℝ 3 . Jakobijská podmínka na X 1 a X 2 zajišťuje podle řetězového pravidla , že tento vektor nezávisí na f .
Pro hladké funkce na povrchu mají vektorová pole (tj. Tečná vektorová pole) důležitou interpretaci jako operátory prvního řádu nebo derivace. Nechť je pravidelný povrch, otevřená podmnožina roviny a souřadnicový graf. Pokud je prostor identifikován pomocí . Podobně identifikuje vektorová pole zapnutá s vektorovými poli zapnutá . Užívání standardních proměnných U a V , vektorové pole má tvar , s a b hladkých funkcí. Pokud je vektorové pole a je hladká funkce, pak je také hladká funkce. Diferenciální operátor prvního řádu je derivace , tj. Splňuje Leibnizovo pravidlo
U vektorových polí X a Y je snadné zkontrolovat, že operátorem je derivace odpovídající vektorovému poli. Říká se tomu Lieova závorka . Je šikmo symetrický a splňuje Jacobiho identitu:
Souhrnně lze říci, že vektorová pole na nebo tvoří algebru Lie pod závorkou Lie.
První a druhá základní forma, operátor tvaru a zakřivení
Nechť S je pravidelný povrch v ℝ 3 . Vzhledem k tomu, místní parametrizace f : V → S a jednotkovou normální vektorové pole n pro f ( V ) , jeden definuje následující předměty, jako jsou reálné hodnotami nebo matrice s hodnotou funkce na V . První základní forma závisí pouze na f , a ne na n . Čtvrtý sloupec zaznamenává způsob, jakým tyto funkce závisí na f , vztažením funkcí E ', F ', G ', L ' atd., Které vyplývají z jiné volby lokální parametrizace, f ': V ' → S , těm, které vznikají pro f . Zde označuje Jakobián matice z f -1 ∘ f ' . Klíčový vztah při vytváření vzorců čtvrtého sloupce je pak
jak následuje řetězové pravidlo .
| Terminologie | Zápis | Definice | Závislost na lokální parametrizaci |
|---|---|---|---|
| První základní forma | E | ||
| F | |||
| G | |||
| Druhá základní forma | L | ||
| M | |||
| N. | |||
| Operátor tvaru | P | ||
| Gaussovo zakřivení | K | ||
| Střední zakřivení | H | ||
| Hlavní zakřivení |
Přímým výpočtem s maticí definující operátor tvaru lze ověřit, že Gaussovo zakřivení je určující pro tvarový operátor, střední zakřivení je stopa operátoru tvaru a hlavní zakřivení jsou vlastní hodnoty operátoru tvaru. ; navíc Gaussovo zakřivení je součinem hlavních zakřivení a střední zakřivení je jejich součtem. Tato pozorování lze také formulovat jako definice těchto objektů. Tato pozorování také jasně ukazují, že poslední tři řádky čtvrtého sloupce bezprostředně navazují na předchozí řádek, protože podobné matice mají identické determinanty, stopy a vlastní čísla. Je důležité poznamenat, že E , G a EG - F 2 jsou nutně pozitivní. Tím je zajištěno, že matice inverzní v definici operátoru tvaru je dobře definována a že hlavní křivky jsou reálná čísla.
Všimněte si také, že negace výběru jednotkového normálního vektorového pole neguje druhou základní formu, operátor tvaru, střední zakřivení a hlavní zakřivení, ale ponechá Gaussovo zakřivení beze změny. V souhrnu to ukázalo, že vzhledem k pravidelnému povrchu S lze Gaussovo zakřivení S považovat za funkci s reálnou hodnotou na S ; vzhledem k volbě jednotkového normálního vektorového pole na všech S jsou dvě hlavní zakřivení a průměrné zakřivení také na S skutečnými funkcemi .
Geometricky, první a druhá základní formy mohou být považovány za poskytování informací o tom, jak f ( u , v ), se pohybuje kolem v ℝ 3 jako ( u , v ), se pohybuje kolem v V . Zejména první základní forma kóduje, jak rychle se f pohybuje, zatímco druhá základní forma kóduje, do jaké míry je její pohyb ve směru normálního vektoru n . Jinými slovy, druhá základní forma v bodě p kóduje délku ortogonálního průmětu od S do tečné roviny k S v p ; zejména dává kvadratickou funkci, která nejlépe odpovídá této délce. Toto myšlení lze upřesnit pomocí vzorců
jak vyplývá přímo z definic základních forem a Taylorovy věty ve dvou dimenzích. Hlavní křivky lze zobrazit následujícím způsobem. V daném bodě P z S , za shromažďování všech rovinách, které obsahují kolmý k linii S . Každá taková rovina má křivku průsečíku se S , kterou lze považovat za křivku roviny uvnitř samotné roviny. Dvě hlavní zakřivení v bodě p jsou maximální a minimální možné hodnoty zakřivení této rovinné křivky v bodě p , protože uvažovaná rovina se otáčí kolem normální čáry.
Následující text shrnuje výpočet výše uvedených veličin vzhledem k Mongeově náplasti f ( u , v ) = ( u , v , h ( u , v )) . Zde h u a h v označují dva parciální deriváty h , s analogickým zápisem pro druhé parciální derivace. Druhá základní forma a všechny následující veličiny se vypočítají relativně k dané volbě jednotkového normálního vektorového pole.
| Množství | Vzorec |
|---|---|
| Jednotkové normální vektorové pole | |
| První základní forma | |
| Druhá základní forma | |
| Operátor tvaru | |
| Gaussovo zakřivení | |
| Střední zakřivení |
Christoffelovy symboly, Gauss -Codazziho rovnice a Theorema Egregium
Nechť S je pravidelný povrch v ℝ 3 . Christoffel symboly přiřazení, aby každé místní nastavení jeho parametrů f : V → S , osm funkce na V , definované
Mohou být také definovány následujícími vzorci, ve kterých n je jednotkové normální vektorové pole podél f ( V ) a L , M , N jsou odpovídajícími složkami druhé základní formy:
Klíčem k této definici je, že ∂ f/∂ u, ∂ f/∂ v, a n tvoří základ ℝ 3 v každém bodě, vzhledem ke kterému každá ze tří rovnic jednoznačně specifikuje Christoffelovy symboly jako souřadnice druhých parciálních derivací f . Volba jednotkové normály nemá žádný vliv na Christoffelovy symboly, protože pokud je n vyměněno za její negaci, pak jsou složky druhé základní formy také negovány, a tak jsou znaky Ln , Mn , Nn ponechány beze změny.
Druhá definice ukazuje v kontextu místních parametrizací, že Christoffelovy symboly jsou geometricky přirozené. Ačkoli vzorce v první definici vypadají méně přirozeně, mají důležitost ukázat, že Christoffelovy symboly lze vypočítat z první základní formy, což z druhé definice není hned patrné. Ekvivalence definic mohou být kontrolovány přímým nahrazením první definici do druhé, a za použití definice E , F , G .
Codazzi rovnice tvrdí, že
Tyto rovnice lze přímo odvodit z výše uvedené druhé definice Christoffelových symbolů; například první Codazziho rovnice se získá diferenciací první rovnice s ohledem na v , druhé rovnice s ohledem na u , odečtením dvou a součtem bodového součinu s n . Gauss rovnice tvrdí, že
Ty mohou být podobně odvozeny jako Codazziho rovnice, přičemž jedna místo Weingartenových rovnic místo toho, aby se bodový součin vzal n . Ačkoli jsou tyto zapsány jako tři samostatné rovnice, jsou totožné, když jsou nahrazeny definice Christoffelových symbolů, pokud jde o první základní formu. Existuje mnoho způsobů, jak zapsat výsledný výraz, jeden z nich odvozený v roce 1852 Brioschi pomocí šikovného použití determinantů:
Když jsou Christoffelovy symboly považovány za definované první základní formou, Gaussova a Codazziho rovnice představují určitá omezení mezi první a druhou základní formou. Zvláště pozoruhodná je Gaussova rovnice, která ukazuje, že Gaussovo zakřivení lze vypočítat přímo z první základní formy, bez potřeby dalších informací; ekvivalentně to říká, že LN - M 2 lze ve skutečnosti zapsat jako funkci E , F , G , i když jednotlivé složky L , M , N nemohou. Toto je známé jako theorema egregium a byl to hlavní objev Carla Friedricha Gausse . Je to zvláště pozoruhodné, když si vzpomeneme na geometrickou definici Gaussova zakřivení S, jak je definována maximálním a minimálním poloměrem oscilujících kruhů; zdá se, že jsou zásadně definovány geometrií toho, jak se S ohýbá do ℝ 3 . Věta nicméně ukazuje, že jejich produkt lze určit z „vnitřní“ geometrie S , která má co do činění pouze s délkami křivek podél S a úhly vytvořenými v jejich průsečících. Jak řekl Marcel Berger :
Tato věta je matoucí. [...] Je to ten typ věty, který mohl čekat desítky let déle, než byl objeven jiným matematikem, protože na rozdíl od mnoha intelektuálních dějin nebyl absolutně ve vzduchu. [...] Podle našich znalostí dnes neexistuje jednoduchý geometrický důkaz theorema egregium.
Rovnice Gauss-Codazzi lze také stručně vyjádřit a odvodit v jazyce spojovacích forem díky Élie Cartanovi . V jazyce tenzorového počtu , využívajícího přirozené metriky a spojení na tenzorových svazcích , lze Gaussovu rovnici zapsat jako H 2 - | h | 2 = R a dvě Codazziho rovnice lze zapsat jako ∇ 1 h 12 = ∇ 2 h 11 a ∇ 1 h 22 = ∇ 2 h 12 ; Komplikované výrazy dělat s Christoffelovy symboly a první základní forma se úplně absorbován do definicích kovariantní tensor derivátu ∇ h a skalární zakřivení R . Pierre Bonnet dokázal, že dvě kvadratické formy splňující Gauss-Codazziho rovnice vždy jednoznačně určují vložený povrch lokálně. Z tohoto důvodu jsou Gauss-Codazziho rovnice často nazývány základními rovnicemi pro vložené povrchy, přičemž přesně identifikují, odkud pocházejí vnitřní a vnější zakřivení. Přiznávají zobecnění povrchů vložených do obecnějších riemannianských variet .
Izometrie
Difeomorfismus mezi otevřenými množinami a na pravidelném povrchu je považován za izometrii, pokud zachovává metriku, tj. První základní formu. Proto je pro každý bod v a tečných vektorů v existují rovnosti
Pokud jde o vnitřní produkt pocházející z první základní formy, lze jej přepsat jako
- .
Na druhé straně lze délku parametrizované křivky vypočítat jako
a pokud křivka leží v , pravidla pro změnu proměnných to ukazují
Naopak pokud zachovává délky všech parametrizovaných v křivkách, je to izometrie. Opravdu, pro vhodnou volbu , tečné vektory a dávat libovolné tečné vektory a . Rovnosti musí platit pro veškerý výběr tečných vektorů a také pro a , takže .
Jednoduchý příklad izometrie poskytují dvě parametrizace a otevřená množina do pravidelných ploch a . Pokud , a , pak je izometrie na .
Válec a rovina uvádějí příklady povrchů, které jsou lokálně izometrické, ale které nelze z topologických důvodů rozšířit na izometrii. Jako další příklad, catenoid a spirálové jsou lokálně izometrické.
Kovarianční deriváty
Tangenciální vektorové pole X na S nabyvatele, do každé p v S , s tangenciálním vektorem X P na S v p . Podle výše uvedené „vnitřní“ definice tečných vektorů pak tangenciální vektorové pole X přiřadí každé lokální parametrizaci f : V → S dvě funkce s reálnou hodnotou X 1 a X 2 na V , takže
pro každý p v S . Jeden říká, že X je hladké, pokud jsou funkce X 1 a X 2 hladké, pro libovolný výběr f . Podle dalších výše uvedených definic tečných vektorů lze také považovat tangenciální vektorové pole X na S za mapu X : S → ℝ 3 tak, že X ( p ) je obsaženo v tangenciálním prostoru T p S ⊂ ℝ 3 pro každé p v S . Jak je to běžné v obecnějším situaci hladkých varietách , tangenciální vektorová pole lze také definovat jako určité diferenciální operátory na prostoru hladkých funkcí na S .
Tyto kovariantní deriváty (nazývané také „tangenciální deriváty“) z Tullio Levi-Civita a Gregorio Ricci-Curbastro poskytují prostředky pro rozlišování hladké tangenciální vektorová pole. Vzhledem k tangenciálnímu vektorovému poli X a tečnému vektoru Y až S na p je kovariantní derivace ∇ Y X určitým tečným vektorem k S v p . Pokud jsou tedy X a Y tangenciální vektorová pole, pak ∇ Y X lze také považovat za tangenciální vektorové pole; iterativně, pokud X , Y a Z jsou tangenciální vektorová pole, lze vypočítat ∇ Z ∇ Y X , což bude další tangenciální vektorové pole. Existuje několik způsobů, jak definovat kovariantní derivát; první níže používá Christoffelovy symboly a „vnitřní“ definici tečných vektorů a druhý je zjevněji geometrický.
Vzhledem k tangenciálnímu vektorovému poli X a tečnému vektoru Y až S na p definujeme ∇ Y X jako tečný vektor k p, který přiřadí lokální parametrizaci f : V → S dvě čísla
kde D ( Y 1 , Y 2 ) je směrový derivát . Toto je často zkráceno v méně těžkopádné formě (∇ Y X ) k = ∂ Y ( X k ) + Y i Γ k
ijX j , využívající Einsteinovu notaci a s umístěním vyhodnocení funkce, které je implicitně chápáno. Vyplývá to ze standardního předpisu v Riemannově geometrii pro získání spojení z Riemannovy metriky . Je zásadním faktem, že vektor
v ℝ 3 je nezávislá na volbě lokální parametrizace f , i když je to poněkud únavné kontrolovat.
Lze také definovat kovariantní derivát následujícím geometrickým přístupem, který nevyužívá Christoffelovy symboly ani lokální parametrizace. Nechť X je vektorové pole na S , vnímané jako funkce S → ℝ 3 . Vzhledem k jakékoli křivce c : ( a , b ) → S lze uvažovat o složení X ∘ c : ( a , b ) → ℝ 3 . Jako mapě mezi euklidovských prostorů, že mohou být rozlišeny na jakékoliv vstupní hodnoty získat prvek ( X ∘ c ) "( t ) z ℝ 3 . Kolmý průmět tohoto vektoru na T c ( t ) S definuje kovariantní derivace ∇ c '( t ) X . Přestože se jedná o velmi geometricky čistou definici, je nutné ukázat, že výsledek závisí pouze na c ′ ( t ) a X , a nikoli na c a X ; pro tento malý technický argument lze použít místní parametrizace.
Z druhé definice není hned zřejmé, že kovariantní diferenciace závisí pouze na první základní formě S ; toto je však bezprostřední z první definice, protože Christoffelovy symboly lze definovat přímo z první základní formy. Je snadné zkontrolovat, zda jsou tyto dvě definice ekvivalentní. Klíčem je, že pokud jde o X 1∂ f/∂ u+ X 2∂ f/∂ vjako ℝ 3 -hodnocená funkce, její diferenciace podél křivky má za následek druhé parciální derivace ∂ 2 f ; Christoffelovy symboly vstupují s ortogonální projekcí do tečného prostoru díky formulaci Christoffelových symbolů jako tangenciálních složek druhých derivací f vzhledem k základu∂ f/∂ u, ∂ f/∂ v, n . Toto je popsáno ve výše uvedené části.
Pravou stranu tří Gaussových rovnic lze vyjádřit pomocí kovariantní diferenciace. Například na pravé straně
lze rozpoznat jako druhou souřadnici
vzhledem k základu ∂ f/∂ u, ∂ f/∂ v, jak lze přímo ověřit pomocí definice kovariantní diferenciace pomocí Christoffelových symbolů. V jazyce Riemannovy geometrie lze toto pozorování také formulovat tak, že říká, že pravé strany Gaussových rovnic jsou různými složkami Ricciho zakřivení spojení Levi-Civita prvního základního tvaru, když je interpretováno jako Riemannova metrika .
Příklady
Revoluční povrchy
Rotační plocha se získá otáčením křivky v rovině xz kolem osy z . Mezi takové povrchy patří koule, válce, kužely, tori a katenoidy . Obecné elipsoidy , hyperboloidy a paraboloidy nejsou. Předpokládejme, že je křivka parametrizována
s s kresleno z intervalu ( a , b ) . Pokud c 1 není nikdy nula, pokud c 1 ′ a c 2 ′ nejsou nikdy obě rovny nule a pokud c 1 a c 2 jsou obě hladké, pak odpovídající plocha otáčení
bude pravidelný povrch v ℝ 3 . Místní parametrizace f : ( a , b ) × (0, 2π) → S je dána vztahem
V poměru k této parametrizaci jsou geometrická data:
| Množství | Vzorec |
|---|---|
| Jednotkové normální vektorové pole | |
| První základní forma | |
| Druhá základní forma | |
| Hlavní zakřivení | |
| Gaussovo zakřivení | |
| Střední zakřivení |
Ve zvláštním případě, kdy je původní křivka parametrizována délkou oblouku, tj. ( C 1 ′ ( s )) 2 + ( c 1 ′ ( s )) 2 = 1 , lze rozlišit a najít c 1 ′ ( s ) c 1 ′ ′ ( S ) + c 2 ′ ( s ) c 2 ′ ′ ( s ) = 0 . Při substituci do Gaussova zakřivení to má člověk zjednodušené
Díky jednoduchosti tohoto vzorce je obzvláště snadné studovat třídu rotačně symetrických ploch s konstantním Gaussovým zakřivením. Redukcí na alternativní případ, že c 2 (s) = s , lze studovat rotačně symetrické minimální povrchy, což má za následek, že jakýkoli takový povrch je součástí roviny nebo zmenšeného katenoidu.
Každá křivka konstantní t na S může být parametrizována jako geodetická; co by konstantního s křivka na S lze parametrizovat jako přímou linií, jestliže a pouze v případě, c 1 '(s) je rovna nule. Geodetika na S se obecně řídí vztahem Clairaut .

Kvadrické povrchy
Zvažte kvadrický povrch definovaný
Tento povrch připouští parametrizaci
Gaussovo zakřivení a střední zakřivení jsou dány vztahem

Regulované povrchy
Vládnutý povrch je takový, který může být generován pohybem přímky v E 3 . Volba přímky na povrchu, tj. Hladká křivka jednotkové rychlosti c ( t ) kolmá k přímkám, a poté výběrem u ( t ) jako jednotkových vektorů podél křivky ve směru přímek, vektor rychlosti v = c t a u uspokojit
Povrch se skládá z bodů
jak se s a t liší.
Pak, pokud
Gaussovské a střední zakřivení jsou dány vztahem
Gaussovo zakřivení ovládaného povrchu zmizí právě tehdy, jsou -li u t a v proporcionální. Tato podmínka je ekvivalentní tomu, že povrch je obalem rovin podél křivky obsahující tečný vektor v a ortogonální vektor u , tj. K povrchu je rozvinutelné podél křivky. Obecněji má povrch v E 3 mizející gaussovské zakřivení v blízkosti bodu právě tehdy, je -li v tomto bodě vyvíjitelný. (V metrice je níže uvedena ekvivalentní podmínka.)
Minimální povrchy
V roce 1760 Lagrange rozšířil Eulerovy výsledky o variačním počtu zahrnujícím integrály v jedné proměnné na dvě proměnné. Měl na mysli následující problém:
Vzhledem k uzavřené křivce v E 3 najděte povrch s křivkou jako hranicí s minimální plochou.
Takový povrch se nazývá minimální povrch .
V roce 1776 Jean Baptiste Meusnier ukázal, že diferenciální rovnice odvozená Lagrangeovým ekvivalentem mizí průměrného zakřivení povrchu:
Povrch je minimální právě tehdy, když zmizí jeho průměrné zakřivení.
Minimální povrchy mají v reálném životě jednoduchou interpretaci: jsou to tvary, které mýdlový film převezme, pokud se drátěný rám ve tvaru křivky ponoří do mýdlového roztoku a poté opatrně nadzvedne. Otázka, zda existuje minimální povrch s danou hranicí, se nazývá Plateauův problém podle belgického fyzika Josepha Plateaua, který v polovině devatenáctého století prováděl experimenty na mýdlových filmech. V roce 1930 dali Jesse Douglas a Tibor Radó kladnou odpověď na Plateauův problém (Douglas získal za tuto práci v roce 1936 jednu z prvních Fieldsových medailí ).
Mnoho explicitní příklady minimálním povrchu jsou známy výslovně, jako je catenoid , do spirálové , na Scherk povrchem a povrchem Enneper . V této oblasti proběhl rozsáhlý výzkum, shrnutý v Osserman (2002) . Zejména výsledek Ossermana ukazuje, že pokud je minimální povrch nerovinný, pak je jeho obraz pod Gaussovou mapou v S 2 hustý .
Povrchy konstantního Gaussova zakřivení

Pokud má povrch konstantní Gaussovo zakřivení, nazývá se to povrch s konstantním zakřivením .
- Jednotková sféra v E 3 má konstantní Gaussovo zakřivení +1.
- Euklidovská rovina i válec mají konstantní Gaussovo zakřivení 0.
- Plochy otáčení s φ tt = φ mají konstantní Gaussovo zakřivení –1. Zvláštní případy se získají tak, že φ ( t ) = C cosh t , C sinh t a C e t . Druhý případ je klasická pseudosféra generovaná otáčením traktrixu kolem centrální osy. V roce 1868 Eugenio Beltrami ukázal, že geometrie pseudosféry přímo souvisí s hyperbolickou rovinou , kterou nezávisle objevili Lobachevsky (1830) a Bolyai (1832). Již v roce 1840 získal F. Minding, Gaussův žák, goniometrické vzorce pro pseudosféru shodné s těmi pro hyperbolickou rovinu. Vnitřní geometrie tohoto povrchu je nyní lépe pochopitelná z hlediska Poincarého metriky na horní poloviční rovině nebo jednotkovém disku a byla popsána jinými modely, jako je Kleinův model nebo hyperboloidní model , získaný uvažováním dvouvrstvého hyperboloid q ( x , y , z ) = −1 v trojrozměrném Minkowského prostoru , kde q ( x , y , z ) = x 2 + y 2 - z 2 .
Každý z těchto povrchů s konstantním zakřivením má tranzitivní Lieovu skupinu symetrií. Tato skupina teoretická skutečnost má dalekosáhlé důsledky, a to tím spíše pozoruhodné vzhledem k ústřední úloze těchto speciálních povrchů hrají v geometrii ploch, vzhledem k Poincaré ‚s uniformization věta (viz níže).
Mezi další příklady povrchů s Gaussovým zakřivením 0 patří kužely , tečné rozvinutelné a obecněji všechny rozvinutelné povrchy.
Lokální metrická struktura
Pro jakýkoli povrch zasazený do euklidovského prostoru dimenze 3 nebo vyšší je možné změřit délku křivky na povrchu, úhel mezi dvěma křivkami a oblast oblasti na povrchu. Tato struktura je nekonečně zakódována v Riemannově metrice na povrchu prostřednictvím liniových a plošných prvků . Klasicky v devatenáctém a na počátku dvacátého století byly brány v úvahu pouze povrchy vložené do R 3 a metrika byla dána jako 2 × 2 pozitivní definitivní matice, která se plynule mění od bodu k bodu v lokální parametrizaci povrchu. Myšlenka lokální parametrizace a změny souřadnic byla později formalizována prostřednictvím současného abstraktního pojmu potrubí , topologického prostoru, kde je hladká struktura dána lokálními grafy na potrubí, přesně tak, jak je dnes planeta Země mapována atlasy . Změny souřadnic mezi různými grafy stejné oblasti musí být plynulé. Stejně jako vrstevnice na mapách v reálném životě kódují změny nadmořské výšky, přičemž se při výpočtu skutečných vzdáleností berou v úvahu lokální zkreslení zemského povrchu, tak riemannianská metrika popisuje vzdálenosti a oblasti „v malém“ v každém místním grafu. V každém lokálním grafu je Riemannova metrika dána hladkým přiřazením 2 × 2 kladné určité matice ke každému bodu; když se vezme jiný graf, matice se transformuje podle jakobijské matice změny souřadnic. Rozdělovač pak má strukturu 2-dimenzionálního riemannianského rozdělovače .
Operátor tvaru
Rozdíl dn o Gauss Pro n může být použita pro definování typu vnějšího zakřivení, známý jako operátor tvar nebo Weingarten mapy. Tento operátor se poprvé objevil implicitně v díle Wilhelma Blaschkeho a později výslovně v pojednání Burali-Fortiho a Burgatiho. Protože v každém bodě x plochy je tečný prostor vnitřním součinovým prostorem , lze tvarový operátor S x definovat jako lineární operátor v tomto prostoru podle vzorce
pro tečné vektory v , w (vnitřní součin dává smysl, protože dn ( v ) a w oba leží v E 3 ). Pravá strana je symetrická ve v a w , takže operátor tvaru je v tangenciálním prostoru samočinný . Vlastní čísla S x jsou pouze hlavní křivky k 1 a k 2 v x . Zejména determinantem tvarového operátoru v bodě je Gaussovo zakřivení, ale obsahuje také další informace, protože průměrné zakřivení je polovinou stopy operátoru tvaru. Střední zakřivení je vnější invariant. Ve vnitřní geometrii je válec vyvíjitelný, což znamená, že každý jeho kus je vnitřně nerozeznatelný od kusu letadla, protože jeho Gaussovo zakřivení zmizí stejně. Jeho průměrné zakřivení však není nulové; z vnějšku se tedy liší od letadla.
Ekvivalentně obsluha tvar může být definován jako lineární operátor na tečných prostorech, S p : T p M → T p M . Pokud n je jednotkové normální pole k M a v je tečný vektor, pak
(neexistuje standardní dohoda, zda v definici použít + nebo -).
Obecně platí, že vlastní vektory a vlastní hodnoty tvarového operátoru v každém bodě určují směry, ve kterých se povrch v každém bodě ohýbá. Vlastní čísla odpovídají hlavním zakřivením povrchu a vlastní vektory jsou odpovídajícími hlavními směry. Hlavní směry určují směry, kterými musí křivka vložená do povrchu cestovat, aby měla maximální a minimální zakřivení, přičemž tyto jsou dány hlavními zakřiveními.
Geodetické křivky na povrchu
Křivky na povrchu, které minimalizují délku mezi koncovými body, se nazývají geodetika ; jsou tvarem, který by měl pružný pás natažený mezi dvěma body. Matematicky jsou popsány pomocí obyčejných diferenciálních rovnic a variačního počtu . Diferenciální geometrie povrchů se točí kolem studia geodetiky. Je stále otevřenou otázkou, zda každá riemannovská metrika na 2-dimenzionálním lokálním grafu pochází z vložení do 3-dimenzionálního euklidovského prostoru: geologická teorie byla použita k prokázání, že to platí v důležitém případě, kdy komponenty metriky jsou analytičtí .
Geodetika
Je -li v grafu pro t v [ a , b ] kusová hladká cesta c ( t ) = ( x ( t ), y ( t )) , je její délka definována
a energii tím
Délka je nezávislá na parametrizaci cesty. Podle Euler -Lagrangeových rovnic , pokud c ( t ) je cesta minimalizující délku, parametrizovaná délkou oblouku , musí splňovat Eulerovy rovnice
kde symboly Christoffel Γk
ij jsou dány
kde g 11 = E , g 12 = F , g 22 = G a g ij je inverzní matice k g ij . Dráha splňující Eulerovy rovnice se nazývá geodetická . Podle Cauchy -Schwarzovy nerovnosti je cesta minimalizující energii jen geodetickou parametrizací délkou oblouku; a pro jakoukoli geodetiku je parametr t úměrný délce oblouku.
Geodetické zakřivení
Geodetické zakřivení k g v bodě křivky c ( t ) , parametrizovány podle délky oblouku, na orientovaném povrchu je definována tak, aby se
kde n ( t ) je „hlavní“ jednotka kolmá ke křivce na povrchu, sestrojená otáčením vektoru tangenty jednotky ċ ( t ) o úhel +90 °.
- Geodetické zakřivení v bodě je vnitřní invariant závislý pouze na metrice poblíž bodu.
- Křivka jednotkové rychlosti na povrchu je geodetická právě tehdy, když její geodetické zakřivení zmizí ve všech bodech křivky.
- Křivka jednotkové rychlosti c ( t ) ve vloženém povrchu je geodetická právě tehdy, je -li její vektor zrychlení c̈ ( t ) k povrchu kolmý.
Geodetické zakřivení přesně měří, jak daleko je křivka na povrchu od geodetické.
Ortogonální souřadnice
Když F = 0 v souřadnicovém grafu, například s geodetickými polárními souřadnicemi diskutovanými níže, obrazy čar rovnoběžných s osami x - a y jsou ortogonální a poskytují ortogonální souřadnice . Pokud H = ( EG ) 1 ⁄ 2 , pak je Gaussovo zakřivení dáno vztahem
Je -li navíc E = 1 , takže H = G 1 ⁄ 2 , pak úhel φ v průsečíku mezi geodetickými ( x ( t ), y ( t )) a přímkou y = konstantní je dán rovnicí
Derivace φ je dána klasickým Gaussovým derivačním vzorcem:
Geodetické polární souřadnice

Jakmile je na povrchu zadána metrika a pevný bod je fixován, existuje unikátní geodetika spojující základní bod s každým dostatečně blízkým bodem. Směr geodetiky v základním bodě a vzdálenost jednoznačně určují druhý koncový bod. Tyto dva bity dat, směr a velikost, tedy určují tečný vektor v základním bodě. Mapa od tečných vektorů ke koncovým bodům plynule zametá sousedství základního bodu a definuje to, co se nazývá „exponenciální mapa“, definující lokální souřadnicový graf v tomto základním bodě. Vymetené sousedství má podobné vlastnosti jako koule v euklidovském prostoru, konkrétně jakékoli dva body v něm jsou spojeny jedinečnou geodetikou. Tato vlastnost se nazývá „geodetická konvexita“ a souřadnice se nazývají „normální souřadnice“. Explicitní výpočet normálních souřadnic lze provést zvážením diferenciální rovnice, kterou geodetika splňuje. Konvexní vlastnosti jsou důsledkem Gaussova lemmatu a jeho zobecnění. Zhruba řečeno, toto lemma říká, že geodetika začínající v základním bodě musí řezat koule s pevným poloměrem se středem na základním bodě v pravých úhlech. Geodetické polární souřadnice se získají kombinací exponenciální mapy s polárními souřadnicemi na tečných vektorech v základním bodě. Gaussovské zakřivení povrchu je pak dáno odchylkou druhého řádu metriky v bodě od euklidovské metriky. Zejména Gaussovo zakřivení je invariantem metriky, Gaussova oslavovaného Theorema Egregium . Pohodlný způsob, jak porozumět zakřivení, pochází z obyčejné diferenciální rovnice, nejprve uvažované Gaussem a později zobecněné Jacobi, vyplývající ze změny normálních souřadnic o dvou různých bodech. Gaussova -Jacobiho rovnice poskytuje další způsob výpočtu Gaussova zakřivení. Geometricky to vysvětluje, co se stane s geodetikou z pevného základního bodu, protože koncový bod se mění podél segmentu malé křivky prostřednictvím dat zaznamenaných v poli Jacobi , vektorovém poli podél geodetiky. Jedno a čtvrt století po Gaussovi a Jacobim Marston Morse poskytl koncepčnější interpretaci Jacobiho pole, pokud jde o druhé derivace energetické funkce na nekonečně dimenzionálním Hilbertově řadě cest.
Exponenciální mapa
Teorie obyčejných diferenciálních rovnic ukazuje, že pokud f ( t , v ) je hladká, pak diferenciální rovnicedv/dt= f ( t , v ) s počáteční podmínkou v (0) = v 0 má jedinečné řešení pro | t | dostatečně malý a řešení hladce závisí na t a v 0 . To znamená, že pro dostatečně malé tečné vektory v daném bodě p = ( x 0 , y 0 ) existuje geodetické c v ( t ) definované na (−2, 2) s c v (0) = ( x 0 , y 0 ) a ċ v (0) = v . Navíc pokud | s | ≤ 1 , pak c sv = c v ( st ) . Exponenciální mapa je definován
- exp p ( v ) = c v (1)
a dává diffeomorfismus mezi diskem ‖ v ‖ < δ a sousedstvím p ; obecněji odeslání mapy ( p , v ) do exp p ( v ) dává místní diffeomorphism na sousedství ( p , p ) . Exponenciální mapa udává normální geodetické souřadnice blízko p .
Výpočet normálních souřadnic
Existuje standardní technika (viz například Berger (2004) ) pro výpočet změny proměnných na normální souřadnice u , v v bodě jako formální rozšíření Taylorovy řady. Pokud jsou souřadnice x , y v místě (0,0) lokálně ortogonální, napište
- x ( u , v ) = αu + L ( u , v ) + λ ( u , v ) +…
- y ( u , v ) = βv + M ( u , v ) + μ ( u , v ) +…
kde L , M jsou kvadratické a λ , μ kubické homogenní polynomy v u a v . Pokud jsou u a v pevné, x ( t ) = x ( tu , tv ) a y ( t ) = y ( tu , tv ) lze považovat za formální řešení řady Eulerových rovnic: toto jednoznačně určuje α , β , L , M , λ a μ .
Gaussovo lemma

V těchto souřadnicích matice g ( x ) splňuje g (0) = I a přímky t ↦ tv jsou geodetické přes 0. Eulerovy rovnice znamenají maticovou rovnici
- g ( v ) v = v ,
klíčový výsledek, obvykle nazývaný Gaussovo lemma . Geometricky to uvádí
geodetika přes 0 prořízla kruhy se středem 0 ortogonálně .
Když vezmeme polární souřadnice ( r , θ ) , vyplývá, že metrika má tvar
- ds 2 = dr 2 + G ( r , θ ) dθ 2 .
V geodetických souřadnicích je snadné zkontrolovat, zda geodetika nulou minimalizuje délku. Topologie na riemannianském rozdělovači je pak dána distanční funkcí d ( p , q ) , konkrétně infimum délek po částech hladkých drah mezi p a q . Tato vzdálenost je lokálně realizována geodetikou, takže v normálních souřadnicích d (0, v ) = ‖ v ‖ . Pokud je poloměr δ dostatečně malý, mírné doostření Gaussova lemmatu ukazuje, že obraz U disku ‖ v ‖ < δ pod exponenciální mapou je geodeticky konvexní , tj. Jakékoli dva body v U jsou spojeny jedinečným geodetickým ležícím zcela uvnitř U .
Theorema Egregium
Gaussova věta Egregium , „Pozoruhodná věta“, ukazuje, že Gaussovo zakřivení povrchu lze vypočítat pouze z hlediska metriky, a je tedy vnitřní invariantem povrchu, nezávislého na jakémkoli izometrickém vložení do E 3 a nezměněné při transformaci souřadnic . Zejména izometrie povrchů zachovávají Gaussovo zakřivení.
Tato věta může být vyjádřena jako expanze výkonové řady metriky, ds , je dána v normálních souřadnicích ( u , v ) jako
- ds 2 = du 2 + dv 2 - K ( u dv - v du ) 2 /12 + ... .
Gaussova -Jacobiho rovnice
Pořízení změnou souřadnic z normálních souřadnic na str normálních souřadnic v blízké bodu q , se získá rovnice Sturm-Liouvilleova splněn H ( r , t Vstup ) = G ( r , t Vstup ) 1 / 2 , objevil Gauss a později generalizované od Jacobi ,
H rr = - KH
Jakobián této změny souřadnic na q je rovno H r . To dává další způsob, jak stanovit vnitřní povahu Gaussova zakřivení. Protože H ( r , θ ) lze interpretovat jako délku čárového prvku ve směru θ , Gaussova -Jacobiho rovnice ukazuje, že Gaussovo zakřivení měří šíření geodetiky na geometrickém povrchu, když se vzdalují od bodu.
Operátor Laplace – Beltrami
Na povrchu s lokální metrikou
kde H 2 = EG - F 2 , Gaussovo zakřivení v bodě je dáno vzorcem
kde r označuje geodetickou vzdálenost od bodu.
V izotermických souřadnicích , nejprve zvažovaných Gaussem, musí být metrika zvláštního tvaru
V tomto případě je operátor Laplace – Beltrami dán
a φ splňuje Liouvilleovu rovnici
Je známo, že izotermické souřadnice existují v sousedství jakéhokoli bodu na povrchu, i když všechny dosavadní důkazy se opírají o netriviální výsledky parciálních diferenciálních rovnic . Pro minimální povrchy existuje elementární důkaz.
Gaussova – Bonnetova věta

Na kouli nebo hyperboloidu je plocha geodetického trojúhelníku , tj. Trojúhelníku, jehož všechny strany jsou geodetické, úměrná rozdílu součtu vnitřních úhlů a π . Konstanta proporcionality je jen Gaussovo zakřivení, konstanta pro tyto povrchy. U torusu je rozdíl nulový, což odráží skutečnost, že jeho Gaussovo zakřivení je nulové. Toto jsou standardní výsledky v sférické, hyperbolické a středoškolské trigonometrii (viz níže). Gauss zobecnil tyto výsledky na libovolný povrch tím, že ukázal, že integrál Gaussova zakřivení uvnitř geodetického trojúhelníku je roven tomuto rozdílu nebo přebytku úhlu. Jeho vzorec ukázal, že Gaussovo zakřivení lze vypočítat v blízkosti bodu jako mez přebytku plochy nad úhlem pro geodetické trojúhelníky smršťující se do bodu. Protože jakýkoli uzavřený povrch lze rozložit na geodetické trojúhelníky, vzorec by mohl být také použit k výpočtu integrálu zakřivení po celém povrchu. Jako zvláštní případ toho, čemu se dnes říká Gaussova – Bonnetova věta , Gauss dokázal, že tento integrál byl pozoruhodně vždy 2π krát celé číslo, topologický invariant povrchu nazývaný Eulerova charakteristika . Tento invariant lze snadno vypočítat kombinatoricky, pokud jde o počet vrcholů, hran a ploch trojúhelníků při rozkladu, nazývaných také triangulace . Tato interakce mezi analýzou a topologií byla předchůdcem mnoha pozdějších výsledků v geometrii, které vyvrcholily Atiyah-Singerovou indexovou větou . Zejména vlastnosti zakřivení omezují topologii povrchu.
Geodetické trojúhelníky
Gauss dokázal, že pokud Δ je geodetický trojúhelník na povrchu s úhly α , β a γ ve vrcholech A , B a C , pak
Ve skutečnosti vezmeme -li geodetické polární souřadnice s počátky A a AB , AC poloměry v polárních úhlech 0 a α :
kde druhá rovnost vyplývá z Gauss – Jacobiho rovnice a čtvrtá z Gaussova derivačního vzorce v ortogonálních souřadnicích ( r , θ ) .
Gaussův vzorec ukazuje, že zakřivení v bodě lze vypočítat jako mez přebytku úhlu α + β + γ - π nad plochou pro postupně menší geodetické trojúhelníky poblíž bodu. Kvalitativně je povrch kladně nebo záporně zakřiven podle znaménka přebytku úhlu pro libovolně malé geodetické trojúhelníky.
Gaussova – Bonnetova věta
Protože každý kompaktně orientovaný 2-variátor M může být triangulován malými geodetickými trojúhelníky, vyplývá z toho
kde χ ( M ) označuje Eulerovu charakteristiku povrchu.
Ve skutečnosti, pokud existují F plochy, E hrany a V vrcholy, pak 3 F = 2 E a levá strana se rovná 2π V - π F = 2π ( V - E + F ) = 2π χ ( M ) .
Toto je oslavovaná Gaussova – Bonnetova věta : ukazuje, že integrál Gaussova zakřivení je topologickým invariantem rozmanitosti, konkrétně Eulerovy charakteristiky. Tuto větu lze interpretovat mnoha způsoby; možná jeden z nejdálnějšího dosahu byl indexový teorém pro eliptický diferenciální operátor na M , jeden z nejjednodušších případů Atiyah-Singerova indexového teorému . Dalším souvisejícím výsledkem, který lze prokázat Gaussovou-Bonnetovou větou, je Poincaré-Hopfova věta o indexu pro vektorová pole na M, která mizí pouze v konečném počtu bodů: součet indexů v těchto bodech se rovná Eulerově charakteristice, kde index bodu je definován následovně: na malém kruhu kolem každé izolované nuly definuje vektorové pole mapu do jednotkové kružnice; index je pouze navíjecí číslo této mapy.)
Zakřivení a vložení
Pokud je Gaussovo zakřivení povrchu M všude kladné, pak je Eulerova charakteristika kladná, takže M je homeomorfní (a tedy diffeomorfní) až S 2 . Pokud je navíc povrch izometricky vložen do E 3 , Gaussova mapa poskytuje explicitní diffeomorfismus. Jak Hadamard poznamenal, v tomto případě je povrch konvexní ; toto kritérium pro konvexitu lze považovat za 2-dimenzionální zobecnění známého druhého derivačního kritéria pro konvexitu rovinných křivek. Hilbert dokázal, že každý izometricky vložený uzavřený povrch musí mít bod pozitivního zakřivení. Uzavřený riemannovský 2-varieta pozitivního zakřivení tedy nikdy nemůže být vložen izometricky do E 3 ; jak však ukázal Adriano Garsia pomocí Beltramiho rovnice pro kvazokonformní mapování , je to vždy možné pro nějakou konformně ekvivalentní metriku.
Povrchy konstantního zakřivení
Tyto jednoduše spojené plochy konstantní zakřivení 0, +1 a -1 jsou euklidovská rovina, koule jednotky v E 3 , a hyperbolické letadlo . Každý z nich má tranzitivní trojrozměrnou Lieovu skupinu izometrií G zachovávajících orientaci , které lze použít ke studiu jejich geometrie. Každá z těchto dvou ne-kompaktní plochy mohou být identifikovány s kvocient G / K , kde K je maximální kompaktní podskupina z G . Zde K je izomorfní na SO (2) . Jakékoli jiné uzavřené Riemannian 2-potrubí M konstantního Gaussova zakřivení, po změně měřítka metriky o konstantní faktor v případě potřeby, bude mít jeden z těchto tří povrchů jako svůj univerzální krycí prostor . V orientable případě je základní skupina Γ z M může být identifikován s torzní bez jednotného podskupiny z G a M pak může být identifikován s dvojitým coset prostoru Γ \ G / K . V případě sféry a euklidovské roviny jsou jedinými možnými příklady samotná sféra a tori získané jako kvocienty R 2 diskrétními podskupinami rank 2. Pro uzavřené povrchy rodu g ≥ 2 má modulový prostor Riemannových povrchů získaný jako Γ proměnnou ve všech takových podskupinách, má skutečný rozměr 6 g - 6 . Podle Poincaréovy uniformizační věty je každé orientovatelné uzavřené 2 potrubí shodné s povrchem s konstantním zakřivením 0, +1 nebo –1. Jinými slovy, vynásobením metrika pozitivním měřítka, Gaussian zakřivení mohou být provedeny, aby se přesně jednu z těchto hodnot (znaménko charakteristiky Eulerovy z M ).
Euklidovská geometrie
V případě euklidovské roviny je skupina symetrie euklidovskou pohybovou skupinou , polopřímým součinem dvojrozměrné skupiny překladů podle skupiny rotací. Geodetika jsou rovné čáry a geometrie je zakódována v elementárních vzorcích goniometrie , jako je kosinové pravidlo pro trojúhelník se stranami a , b , c a úhly α , β , γ :
Ploché tori mohou být získány tím, že kvocient z R 2, pomocí mříží , tedy volný abelian podskupinu hodnosti 2. Tyto uzavřené povrchy nemají izometrické embeddings v E 3 . Přesto připouštějí izometrické vložení do E 4 ; v nejjednodušším případě to vyplývá ze skutečnosti, že torus je součinem dvou kruhů a každý kruh může být izometricky vložen do E 2 .
Sférická geometrie
Izometrická skupina jednotkové sféry S 2 v E 3 je ortogonální skupina O (3) , přičemž rotační skupina SO (3) jako podskupina izometrií zachovává orientaci. Je to přímý součin SO (3) s antipodální mapou , která posílá x do - x . Skupina SO (3) působí na S 2 přechodně . Stabilizátor podskupina jednotkové vektoru (0,0,1), mohou být identifikovány s tak (2) , tak, že S 2 = SO (3) / SO (2) .
Geodetika mezi dvěma body koule jsou velké kruhové oblouky s těmito danými koncovými body. Pokud body nejsou antipodální, je mezi body jedinečná nejkratší geodetická. Geodetiku lze také teoreticky popsat jako skupinu: každá geodetická přes severní pól (0,0,1) je oběžná dráha podskupiny rotací kolem osy protipodálními body na rovníku.
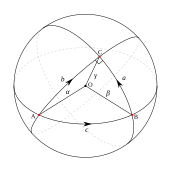
Sférický trojúhelník je geodetická trojúhelník na kouli. Je definován body A , B , C na kouli se stranami BC , CA , AB vytvořenými z velkých kruhových oblouků o délce menší než π . Pokud jsou délky stran a , b , c a úhly mezi stranami α , β , γ , pak sférický kosinový zákon říká, že
Plocha trojúhelníku je dána vztahem
- Plocha = α + β + γ - π .
Pomocí stereografické projekce ze severního pólu lze kouli identifikovat s rozšířenou komplexní rovinou C ∪ {∞} . Explicitní mapa je dána znakem
Podle této korespondence každé otočení S 2 odpovídá Möbiově transformaci v SU (2) , jedinečné až k podpisu. S ohledem na souřadnice ( u , v ) v komplexní rovině se sférická metrika stává
Jednotková sféra je jedinečná uzavřená orientovatelná plocha s konstantním zakřivením +1. Podíl SO (3)/O (2) lze identifikovat se skutečnou projektivní rovinou . Je neorientovatelný a může být popsán jako kvocient S 2 pomocí antipodální mapy (násobení -1). Koule je jednoduše spojena, zatímco skutečná projektivní rovina má základní skupinu Z 2 . V konečné podskupiny tak (3) , odpovídající konečné podskupiny O (2) a symetrie skupin platonickými pevných látek , nejsou volně působit na S 2 , takže odpovídající kvocienty nejsou 2-variety, jen orbifolds .
Hyperbolická geometrie

Neeuklidovská geometrie byla poprvé projednána v dopisech Gaussa, který na přelomu devatenáctého století provedl rozsáhlé výpočty, které, i když byly v soukromém oběhu, se rozhodl nevydávat do tisku. V roce 1830 Lobachevsky a nezávisle na tom v roce 1832 Bolyai , syn jednoho Gaussova zpravodaje, publikoval syntetické verze této nové geometrie, za což byly ostře kritizovány. Nicméně až v roce 1868 Beltrami, následovaný Kleinem v roce 1871 a Poincaré v roce 1882, poskytl konkrétní analytické modely toho, co Klein nazval hyperbolická geometrie . Objevily se čtyři modely 2-dimenzionální hyperbolické geometrie:
- model Beltrami-Klein ;
- disk Poincaré ;
- Poincaré horní polorovina ;
- hyperboloid Model of Wilhelm Killing v 3-rozměrný Minkowski prostor .
První model založený na disku má tu výhodu, že geodetika jsou vlastně úsečky (tedy průsečíky euklidovských čar s otevřeným jednotkovým diskem). Poslední model má tu výhodu, že dává konstrukci, která je zcela rovnoběžná s jednotkovou sférou v 3-dimenzionálním euklidovském prostoru. Vzhledem k jejich aplikaci v komplexní analýze a geometrii jsou však nejrozšířenější modely Poincaré: jsou zaměnitelné díky Möbiusovým transformacím mezi diskem a horní polorovinou.
Nechat
být Poincaré disk v komplexní rovině s Poincaré metrikou
V polárních souřadnicích ( r , θ ) je metrika dána vztahem
Délka křivky γ : [ a , b ] → D je dána vzorcem
Skupina G = SU (1,1) daná vztahem
působí přechodně Möbiusovými transformacemi na D a podskupina stabilizátoru 0 je skupina rotace
Skupina kvocientů SU (1,1)/± I je skupina izometrií D zachovávajících orientaci . Jakékoli dva body z , w v D jsou spojeny jedinečnou geodetikou, danou částí kruhu nebo přímky procházející z a w a ortogonální k hraniční kružnici. Vzdálenost mezi z a w je dána vztahem
Zejména d (0, r ) = 2 tanh -1 r a c ( t ) =1/2tanh t je geodetický přes 0 podél skutečné osy, parametrizovaný délkou oblouku.
Topologie definovaná touto metrikou je ekvivalentní obvyklé euklidovské topologii, i když jako metrický prostor ( D , d ) je úplný.
Hyperbolické trojúhelník je geodetická trojúhelník tato metrika: všechna tři body v D jsou vrcholy hyperbolické trojúhelníku. Pokud mají strany délku a , b , c s odpovídajícími úhly α , β , γ , pak hyperbolické kosinusové pravidlo uvádí, že
Plocha hyperbolického trojúhelníku je dána vztahem
- Plocha = π - α - β - γ .
Disk jednotky a horní polorovina
jsou konformně ekvivalentní Möbiusovými transformacemi
V rámci této korespondence působení SL (2, R), které Möbius transformací na H odpovídá SU (1,1) na D . Metrika na H se stává
Protože čáry nebo kruhy jsou zachovány pod Möbiusovými transformacemi, geodetika je opět popsána čarami nebo kruhy kolmými ke skutečné ose.
Jednotkový disk s metrikou Poincaré je jedinečný jednoduše připojený orientovaný 2-dimenzionální riemannianský rozdělovač s konstantním zakřivením −1. Jakýkoli orientovaný uzavřený povrch M s touto vlastností má D jako svůj univerzální krycí prostor. Jeho základní skupiny mohou být identifikovány s torzním bez concompact podskupiny y z SU (1,1) , a to takovým způsobem, že
V tomto případě Γ je finálně představená skupina . Generátory a vztahy jsou kódovány v geodesically konvexní základní geodetické polygonu v D (nebo H ) odpovídající geometricky do uzavřených geodetiky na M .
Příklady .
- Bolza povrch rodu 2;
- Klein quartic rodu 3;
- MacBeath povrch rodu 7;
- První Hurwitz triplet rodu 14.
Uniformizace
Vzhledem k orientované uzavřené ploše M s Gaussovým zakřivením K lze metriku na M konformně změnit jejím měřítkem o faktor e 2 u . Nové Gaussovo zakřivení K ' je pak dáno vztahem
kde Δ je Laplacian pro původní metriku. Abychom tedy ukázali, že daný povrch je konformně ekvivalentní metrice s konstantním zakřivením K ′ , stačí vyřešit následující variantu Liouvilleovy rovnice :
Když M má Eulerovu charakteristiku 0, je také pro torus odlišná , K ′ = 0 , takže to znamená řešení
Podle standardní eliptické teorie je to možné, protože integrál K nad M je nulový, podle Gaussovy – Bonnetovy věty.
Když má M negativní Eulerovu charakteristiku, K ′ = −1 , rovnice, kterou je třeba vyřešit, je:
Pomocí kontinuity exponenciální mapy na Sobolevově prostoru díky Neilu Trudingerovi lze tuto nelineární rovnici vždy vyřešit.
Nakonec v případě 2-sféry platí K ′ = 1 a rovnice se stává:
Doposud nebyla tato nelineární rovnice analyzována přímo, ačkoli klasické výsledky, jako je Riemann-Rochova věta, naznačují, že vždy má řešení. Metoda Ricciho toku , vyvinutá Richardem S. Hamiltonem , poskytuje další důkaz existence na základě nelineárních parciálních diferenciálních rovnic k prokázání existence. Ve skutečnosti je tok Ricci na konformních metrikách na S 2 definován na funkcích u ( x , t ) pomocí
Po omezeném čase Chow ukázal, že K 'se stává kladným; předchozí výsledky Hamiltona by pak mohly být použity k ukázání, že K ' konverguje k +1. Před těmito výsledky na Ricciho toku Osgood, Phillips & Sarnak (1988) dali alternativní a technicky jednodušší přístup k uniformizaci na základě toku na Riemannově metrice g definovaného log det Δ g .
Jednoduchý důkaz využívající pouze eliptické operátory objevený v roce 1988 lze nalézt v Ding (2001) . Nechť G být funkce Greena na S 2 splňující delta G = 1 + 4π delta P , kde δ P je bod měření v pevném bodě P z S 2 . Rovnice Δ v = 2 K - 2 , má hladké řešení v , protože pravá strana má integrál 0 podle Gauss -Bonnetovy věty. Tak φ = 2 G + V splňuje delta φ = 2 K od P . Z toho vyplývá, že g 1 = e φ g je úplná metrika konstantního zakřivení 0 na komplementu P , který je tedy izometrický k rovině. Skládání se stereografické projekce , to znamená, že tam je hladká funkce u tak, že e 2 u g má Gaussian zakřivení +1 na komplementu P . Funkce u se automaticky rozšíří na hladkou funkci na celém S 2 .
Riemannovské spojení a paralelní doprava

Klasický Gaussův přístup k diferenciální geometrii povrchů byl standardním elementárním přístupem, který předcházel vzniku konceptů Riemannova potrubí iniciovaného Bernhardem Riemannem v polovině devatenáctého století a spojení vyvinutého Tulliem Levi-Civitou , Élie Cartanem a Hermannem Weyl na počátku dvacátého století. Pojem spojení, kovariantní derivace a paralelní transport poskytl koncepčnější a jednotnější způsob chápání zakřivení, což umožnilo nejen zobecnění vyšších dimenzionálních variet, ale také poskytlo důležitý nástroj pro definování nových geometrických invariantů, nazývaných charakteristické třídy . Přístup využívající kovariantní derivace a spojení je v dnešní době uplatňován v pokročilejších učebnicích.
Kovarianční derivát
Spojení na povrchu lze definovat z různých ekvivalentních, ale stejně důležitých hledisek. Připojení Riemannian nebo připojení Levi-Civita . je snad nejsnáze pochopitelný z hlediska zvedání vektorových polí , považovaných za diferenciální operátory prvního řádu působící na funkce na sběrném potrubí, na diferenciální operátory na tangentovém svazku nebo rámcovém svazku . V případě vloženého povrchu je zdvih na operátor na vektorových polích, nazývaný kovarianční derivát , velmi jednoduše popsán z hlediska ortogonální projekce. Ve skutečnosti, vektorové pole na povrchu vložené do R 3, může být považována za funkci z povrchu do R 3 . Další vektorové pole funguje jako komponenta diferenciálního operátoru. Výsledné vektorové pole nebude tečné k povrchu, ale toto lze korigovat jeho kolmým průmětem na tečný prostor v každém bodě povrchu. Jak si Ricci a Levi-Civita uvědomili na přelomu dvacátého století, tento proces závisí pouze na metrice a lze jej lokálně vyjádřit pomocí symbolů Christoffela.
Paralelní doprava
Paralelní transport tečných vektorů po křivce na povrchu byl dalším významným pokrokem subjektu, a to díky Levi-Civita . To se vztahuje k dříve pojmu kovariantní derivace, protože to je monodromy z obyčejné diferenciální rovnice na křivce definované kovariantní derivace vzhledem k vektoru rychlosti křivky. Paralelní transport po geodetice, „přímky“ povrchu, lze také snadno přímo popsat. Vektor v tečné rovině je transportován po geodetice jako jedinečné vektorové pole s konstantní délkou a svírající konstantní úhel s vektorem rychlosti geodetiky. Pro obecnou křivku musí být tento proces upraven pomocí geodetického zakřivení, které měří, jak daleko se křivka odchyluje od geodetické.
Vektorové pole v ( t ) podél křivky jednotkové rychlosti c ( t ) s geodetickým zakřivením k g ( t ) je údajně rovnoběžné podél křivky, pokud
- má konstantní délku
- splňuje úhel θ ( t ) , který svírá s vektorem rychlosti ċ ( t )
Tím se znovu zachytí pravidlo pro paralelní transport po geodetické nebo po částech geodetické křivce, protože v takovém případě k g = 0 , takže úhel θ ( t ) by měl zůstat konstantní na jakémkoli geodetickém segmentu. Následuje existence paralelního transportu, protože θ ( t ) lze vypočítat jako integrál geodetického zakřivení. Protože to tedy závisí kontinuálně na L 2 normě k g , vyplývá, že paralelní transport pro libovolnou křivku lze získat jako limit paralelního transportu na aproximaci kusových geodetických křivek.
Spojení lze tedy popsat pomocí zdvihacích cest v potrubí k cestám v tangenciálním nebo ortonormálním rámcovém svazku, čímž se formalizuje klasická teorie „ pohyblivého rámce “, preferovaná francouzskými autory. Výtahy smyček kolem bodu vedou v tomto bodě ke skupině holonomů . Gaussovo zakřivení v bodě lze obnovit z paralelního transportu kolem stále malých smyček v bodě. Rovnoměrně lze zakřivení vypočítat přímo na nekonečně malé úrovni pomocí Lieových závorek zvednutých vektorových polí.

Připojení 1-forma
Přístup Cartana a Weyl, pomocí připojení 1-formy na rámu svazku z M , poskytuje třetí způsob, jak pochopit Riemannově spojení. Všimli si, že paralelní transport diktuje, že cesta na povrchu se zvedne na cestu ve svazku rámců, takže její tečné vektory leží ve speciálním podprostoru kodimenze jeden v trojrozměrném tangentním prostoru rámcového svazku. Projekce do tohoto podprostoru je definována diferenciální 1 formou ve svazku ortonormálních rámců, formou připojení . To umožnilo zakřivení vlastností povrchu v diferenciálních formách na svazku rámců a vzorcích zahrnujících jejich vnější deriváty .
Tento přístup je obzvláště jednoduchý pro vložený povrch. Díky výsledku Kobayashiho (1956) je spojení 1-forma na povrchu zasazeném do euklidovského prostoru E 3 pouze tahem za Gaussovou mapou formy spojení 1 na S 2 . Pomocí identifikace S 2 s homogenním prostorem SO (3)/SO (2) je spojení 1-forma pouze součástí Maurer-Cartan 1-formy na SO (3) .
Globální diferenciální geometrie povrchů
Ačkoli charakterizace zakřivení zahrnuje pouze lokální geometrii povrchu, existují důležité globální aspekty, jako je Gaussova – Bonnetova věta , uniformizační věta , von Mangoldtova-Hadamardova věta a věta o vložitelnosti. Existují i další důležité aspekty globální geometrie povrchů. Tyto zahrnují:
- Poloměr injektivity definovaný jako největší r tak, že dva body ve vzdálenosti menší než r spojí jedinečná geodetika. Wilhelm Klingenberg v roce 1959 dokázal, že poloměr injektivity uzavřeného povrchu je níže ohraničen minimem δ =π/√ sup Ka délka jeho nejmenší uzavřené geodetiky. Tím se zlepšila Bonnetova věta, která v roce 1855 ukázala, že průměr uzavřeného povrchu kladného Gaussova zakřivení je vždy ohraničen nahoře δ ; jinými slovy, geodetika realizující metrickou vzdálenost mezi dvěma body nemůže mít délku větší než δ .
- Tuhost . V roce 1927 Cohn-Vossen dokázal, že dva ovaloidy -uzavřené povrchy s kladným Gaussovým zakřivením-, které jsou izometrické, se nutně shodují izometrií E 3 . Navíc uzavřený vložený povrch s kladným Gaussovým zakřivením a konstantním průměrným zakřivením je nutně koule; podobně uzavřený zapuštěný povrch konstantního Gaussova zakřivení musí být koule (Liebmann 1899). Heinz Hopf v roce 1950 ukázal, že uzavřený vložený povrch s konstantním průměrným zakřivením a rodem 0, tj. Homeomorfní pro sféru, je nutně koulí; o pět let později Alexandrov odstranil topologický předpoklad. V 80. letech Wente sestrojil ponořené tori konstantního průměrného zakřivení v euklidovském 3-prostoru.
- Carathéodory dohad : Tato domněnka uvádí, že uzavřený konvexní třikrát diferencovatelný povrch připouští alespoň dva umbilické body . První práce na této domněnce byla v roce 1924 Hansem Hamburgerem , který poznamenal, že to vyplývá z následujícího silnějšího tvrzení: poloviční celočíselný hodnotený index hlavní zakřivení foliace izolovaného pupku je nanejvýš jeden.
- Nulové Gaussovo zakřivení : kompletní plocha v E 3 s nulovým Gaussovým zakřivením musí být válec nebo rovina.
- Hilbertova věta (1901): žádný kompletní povrch s konstantním negativním zakřivením nelze izometricky ponořit do E 3 .
- Willmore dohad . Tato domněnka uvádí, že integrál druhé mocniny středního zakřivení torusu ponořeného do E 3 by měl být ohraničen níže 2π 2 . Je známo, že integrál je Moebiusův invariant. Vyřešili to v roce 2012 Fernando Codá Marques a André Neves .
- Izoperimetrické nerovnosti . V roce 1939 Schmidt dokázal, že klasická izoperimetrická nerovnost pro křivky v euklidovské rovině platí také pro sféru nebo v hyperbolické rovině: konkrétně ukázal, že mezi všemi uzavřenými křivkami ohraničujícími doménu pevné oblasti je obvod minimalizován tím, kdy křivka je kruh pro metriku. V jedné dimenzi výše je známo, že mezi všemi uzavřenými povrchy v E 3 vznikajícími jako hranice ohraničené oblasti jednotkového objemu je plocha povrchu pro euklidovskou kouli minimalizována.
- Systolické nerovnosti pro křivky na plochách . Vzhledem k uzavřenému povrchu je jeho systola definována jako nejmenší délka jakékoli nekontrakční uzavřené křivky na povrchu. V roce 1949 Loewner prokázal torusovou nerovnost pro metriky na torusu, konkrétně že oblast torusu nad čtvercem jeho systoly je ohraničena níže√ 3/2, s rovností v plochém (konstantním zakřivení) případě. Podobný výsledek je dán nerovností Pu pro skutečnou projektivní rovinu z roku 1952 s dolní hranicí2/πtaké dosaženo v případě konstantního zakřivení. Pro Kleinovu láhev později získali Blatter a Bavard dolní hranici√ 8/π. U uzavřeného povrchu rodu g Hebda a Burago ukázali, že poměr je ohraničen níže1/2. O tři roky později našel Michail Gromov dolní hranici danou konstantními časy g 1 / 2 , i když to není optimální. Asymptoticky ostré horní a dolní hranice dané konstantními časyG/(log g ) 2jsou způsobeny Gromovem a Buserem-Sarnakem a lze je najít v Katz (2007) . Existuje také verze pro metriky na sféře, která pro systolu bere délku nejmenší uzavřené geodetiky . Gromov předpokládal spodní hranici1/2 √ 3 v roce 1980: zatím nejlepším výsledkem je spodní hranice 1/8 získala Regina Rotman v roce 2006.
Průvodce čtením
Jeden z nejkomplexnějších úvodních průzkumů na toto téma, mapující historický vývoj od doby před Gaussem po moderní dobu, je od Bergera (2004) . Účty klasické teorie jsou uvedeny v Eisenhart (2004) , Kreyszig (1991) a Struik (1988) ; dostupnější by mohly být modernější bohatě ilustrované vysokoškolácké učebnice Graye, Abbeny a Salamona (2006) , Pressley (2001) a Wilsona (2008) . Přístupný popis klasické teorie lze nalézt v Hilbert & Cohn-Vossen (1952) . Sofistikovanější ošetření na úrovni absolventů pomocí riemannianského spojení na povrchu lze nalézt v Singer & Thorpe (1967) , do Carmo (2016) a O'Neill (2006) .
Viz také
Poznámky
Reference
- Andrews, Ben; Bryan, Paul (2010), „Hranice zakřivení izoperimetrickým porovnáním pro normalizovaný Ricciho tok na dvou sférách“, Calc. Var. Dílčí diferenciální rovnice , 39 (3–4): 419–428, arXiv : 0908,3606 , doi : 10,1007/s00526-010-0315-5
- Arnold, VI (1989), Matematické metody klasické mechaniky , Absolventské texty z matematiky, 60 (2. vyd.), New York: Springer-Verlag, ISBN 978-0-387-90314-9; z ruštiny přeložili K. Vogtmann a A. Weinstein.
- Berger, Marcel (2004), Panoramatický pohled na riemannianskou geometrii , Springer-Verlag, ISBN 978-3-540-65317-2
- Berger, Melvyn S. (1977), nelinearita a funkční analýza , Academic Press, ISBN 978-0-12-090350-4
- Bonola, Roberto; Carslaw, HS; Enriques, F. (1955), Non-Euclidean Geometry: Kritická a historická studie jejího vývoje , Dover, ISBN 978-0-486-60027-7
- Boothby, William M. (1986), Úvod do diferencovatelných variet a Riemannovy geometrie , Čistá a aplikovaná matematika, 120 (2. vyd.), Academic Press, ISBN 0121160521
- Cartan, Élie (1983), Geometry of Riemannian Spaces , Math Sci Press, ISBN 978-0-915692-34-7; přeloženo z 2. vydání Leçons sur la géométrie des espaces de Riemann (1951) od Jamese Glazebrooka.
- Cartan, Élie (2001), Riemannian Geometry in an Orthogonal Frame (z přednášek pořádaných É Cartanem na Sorbonně v letech 1926-27) (PDF) , World Scientific, ISBN 978-981-02-4746-1; z ruštiny přeložil VV Goldberg s předmluvou SS Chern .
- Cartan, Henri (1971), Calcul Differentiel (ve francouzštině), Hermann , ISBN 9780395120330
- Chen, Xiuxiong; Lu, Peng; Tian, Gang (2006), „Poznámka k uniformizaci povrchů Riemann proudem Ricci“, Proč. AMS , 134 (11): 3391–3393, doi : 10,1090/S0002-9939-06-08360-2
- Chern, SS (1967), Curves and Surfaces in Euclidean Spaces , MAA Studies in Mathematics, Mathematical Association of America
- Chow, B. (1991), „The Ricci flow on a 2-sphere“, J. Diff. Geom. , 33 (2): 325–334, doi : 10,4310/jdg/1214446319
- Courant, Richard (1950), Dirichletův princip, Konformní mapování a minimální povrchy , John Wiley & Sons, ISBN 978-0-486-44552-6
- Darboux, Gaston , Leçons sur la théorie générale des povrchy , Gauthier-Villars Svazek I (1887) , svazek II (1915) [1889] , svazek III (1894) , svazek IV (1896) .
- Ding, W. (2001), „Důkaz uniformizační věty o S 2 “, J. Parciální diferenciální rovnice , 14 : 247–250
- do Carmo, Manfredo P. (2016), Differential Geometry of Curves and Surfaces (revised & updated 2. ed.), Mineola, NY: Dover Publications, Inc., ISBN 0-486-80699-5
- do Carmo, Manfredo (1992), Riemannian geometry , Mathematics: Theory & Applications, Birkhäuser, ISBN 0-8176-3490-8
- Eisenhart, Luther Pfahler (2004), Pojednání o diferenciální geometrii křivek a povrchů (dotisk vydání z roku 1909), Dover Publications, Inc., ISBN 0-486-43820-1
- Euler, Leonhard (1760), „Recherches sur la courbure des povrchy“ , Mémoires de l'Académie des Sciences de Berlin (publikováno 1767), 16 : 119–143.
- Euler, Leonhard (1771), „De solidis quorum superficiem in planum explicare licet“ , Novi Commentarii Academiae Scientiarum Petropolitanae (publikováno 1772), 16 : 3–34.
-
Gauss, Carl Friedrich (1902), General Investigations of Curved Surfaces of 1825 and 1827 , Princeton University Librarypřeložili AM Hiltebeitel a JC Morehead; "Disquisitiones generales circa superficies curvas" , Commentationes Societatis Regiae Scientiarum Gottingesis Recentiores Vol. VI (1827), s. 99–146.
- Gauss, Carl Friedrich (1965), General Investigations of Curved Surfaces , přeložil AM Hiltebeitel; JC Morehead, Hewlett, NY: Raven Press, OCLC 228665499.
- Gauss, Carl Friedrich (2005), General Investigations of Curved Surfaces , edited with a new Introduction and notes by Peter Pesic, Mineola, NY: Dover Publications, ISBN 978-0-486-44645-5.
- Gray, Alfred; Abbena, Elsa; Salamon, Simon (2006), Modern Differential Geometry of Curves And Surfaces With Mathematica® , Studies in Advanced Mathematics (3rd ed.), Boca Raton, FL: Chapman & Hall/CRC, ISBN 978-1-58488-448-4
- Han, Qing; Hong, Jia-Xing (2006), Isometric Embedding of Riemannian Manifolds in Euclidean Spaces , American Mathematical Society, ISBN 978-0-8218-4071-9
- Helgason, Sigurdur (1978), Differential Geometry , Lie Groups, and Symmetric Spaces , Academic Press, New York, ISBN 978-0-12-338460-7
- Hilbert, David ; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2. vyd.), New York: Chelsea, ISBN 978-0-8284-1087-8
- Hitchin, Nigel (2013), Geometry of Surfaces (PDF)
- Hopf, Heinz (1989), Přednášky o diferenciální geometrii ve velkém , Přednášky z matematiky, 1000 , Springer-Verlag, ISBN 978-3-540-51497-8
- Imayoshi, Y .; Taniguchi, M. (1992), An Introduction to Techmüller spaces , Springer-Verlag, ISBN 978-0-387-70088-5
- Ivey, Thomas A .; Landsberg, JM (2003), Cartan for Beginners: Differential Geometry via Moving Frames and Exterior Systems , Graduate Studies in Mathematics, 61 , American Mathematical Society, ISBN 978-0-8218-3375-9
- Katz, Mikhail G. (2007), Systolická geometrie a topologie , matematické průzkumy a monografie, 137 , American Mathematical Society, ISBN 978-0-8218-4177-8
- Kobayashi, Shoshichi (1956), „Induced connections and inbedded Riemannian space“, Nagoya Math. J. , 10 : 15–25, doi : 10,1017/S0027763000000052
- Kobayashi, Shoshichi (1957), „Theory of connections“, Annali di Matematica Pura ed Applicata , Series 4, 43 : 119–194, doi : 10.1007/BF02411907,
- Kobayashi, Shoshichi; Nomizu, Katsumi (1963), Foundations of Differential Geometry, Vol. Já , Wiley Interscience, ISBN 978-0-470-49648-0
- Kobayashi, Shoshichi; Nomizu, Katsumi (1969), Foundations of Differential Geometry, Vol. II , Wiley Interscience, ISBN 978-0-470-49648-0
- Kreyszig, Erwin (1991), Differential Geometry , Dover, ISBN 978-0-486-66721-8
- Kühnel, Wolfgang (2006), Differential Geometry: Curves - Surfaces - Manifolds , American Mathematical Society, ISBN 978-0-8218-3988-1
- Levi-Civita, Tullio (1917), „Nozione di parallelismo in una varietà qualunque“ (PDF) , Rend. Circ. Rohož. Palermo , 42 : 173–205, doi : 10,1007/BF03014898
- O'Neill, Barrett (2006), Elementární diferenciální geometrie (revidované 2. vydání.), Amsterdam: Elsevier/Academic Press, ISBN 0-12-088735-5
- Osgood, B .; Phillips, R .; Sarnak, P. (1988), "Extremals of determinants of Laplacians", J. Funct. Anální. , 80 : 148–211, doi : 10,1016/0022-1236 (88) 90070-5
- Osserman, Robert (2002), Průzkum minimálních povrchů , Dover, ISBN 978-0-486-49514-9
- Ian R. Porteous (2001) Geometrická diferenciace: pro inteligenci křivek a povrchů , Cambridge University Press ISBN 0-521-00264-8 .
- Pressley, Andrew (2001), Elementární diferenciální geometrie , Springer Pregraduate Mathematics Series, Springer-Verlag, ISBN 978-1-85233-152-8
- Sacks, J .; Uhlenbeck, Karen (1981), „Existence minimálního ponoření 2 koulí“, Ann. matematiky. , 112 (1): 1–24, doi : 10,2307/1971131 , JSTOR 1971131
- Singer, Isadore M .; Thorpe, John A. (1967), Lecture Notes on Elementary Topology and Geometry , Springer-Verlag, ISBN 978-0-387-90202-9
- Spivak, Michael (1965), Kalkulus na varietách. Moderní přístup ke klasickým větám pokročilého počtu , WA Benjamin
- Stillwell, John (1996), Sources of Hyperbolic Geometry , American Mathematical Society, ISBN 978-0-8218-0558-9
- Struik, Dirk (1987), Concise History of Mathematics (4th ed.), Dover Publications, ISBN 0486602559
- Struik, Dirk J. (1988), Přednášky o klasické diferenciální geometrii (dotisk 2. vyd.), New York: Dover Publications, Inc., ISBN 0-486-65609-8
- Taylor, Michael E. (1996a), Parciální diferenciální rovnice II: Kvalitativní studie lineárních rovnic , Springer-Verlag, ISBN 978-1-4419-7051-0
- Taylor, Michael E. (1996b), Parciální diferenciální rovnice III: Nelineární rovnice , Springer-Verlag, ISBN 978-1-4419-7048-0
- Thorpe, John A. (1994), Elementární témata v diferenciální geometrii , bakalářské texty z matematiky, Springer-Verlag, ISBN 0387903577
- Toponogov, Victor A. (2005), Differential Geometry of Curves and Surfaces: A Concise Guide , Springer-Verlag, ISBN 978-0-8176-4384-3
- Valiron, Georges (1986), The Classical Differential Geometry of Curves and Surfaces , Math Sci Press, ISBN 978-0-915692-39-2 Plný text knihy
- Warner, Frank W. (1983), Foundations of differentiable manifolds and Lie groups , Graduate Texts in Mathematics, 94 , Springer, ISBN 0-387-90894-3
- Wells, RO (2017), Differential and complex geometry: origins, abstractions and embeddings , Springer, ISBN 9783319581842
- Wilson, Pelham (2008), Curved Space: From Classical Geometries to Elementary Differential Geometry , Cambridge University Press, ISBN 978-0-521-71390-0
externí odkazy
-
 Média související s diferenciální geometrií povrchů na Wikimedia Commons
Média související s diferenciální geometrií povrchů na Wikimedia Commons
























![{\ displaystyle [X, Y] = XY-YX}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838f73010b4f791eeaf245317fb4b6e07c45d741)
![[X, Y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/94470b44d283fde62130212956058ca6b727da37)
![{\ Displaystyle [X, Y] =-[Y, X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c433e248c0c7e659ef3f2d9df64d8c7505630bc)
![{\ Displaystyle [[X, Y], Z]+[[Y, Z], X]+[[Z, X], Y] = 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d5d5018bd0a276d74259b92a5403824cd982e7)


















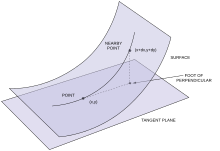






























































![{\ Displaystyle K =-{\ beta ^{2} \ over ((s- \ alpha) ^{2}+\ beta ^{2}) ^{2}}, \, \, K_ {m} =- {r [(s- \ alpha) ^{2}+\ beta ^{2})]+\ beta _ {t} (s- \ alpha)+\ beta \ alpha _ {t} \ přes [(s- \ alpha)^{2}+\ beta^{2}]^{\ frac {3} {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff1ab2130e1d570ae5585c216637fb7661847192)










![{\ Displaystyle K =-{1 \ přes 2H} \ left [\ partial _ {x} \ left ({\ frac {G_ {x}} {H}} \ right)+\ partial _ {y} \ left ( {\ frac {E_ {y}} {H}} \ right) \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa6e6e49b1e0f474132e77018b4d8a8fc78a853d)